高校数学の数学Aで突然現れるなぞの数式
0!=1
は?
0じゃないの?
なんで1になるの?
その疑問、ごもっとも。
僕もそう思ったうちの一人だからです。
0!=1
なぜこう定義するのか。
その意味を解説します。
規則性に基づく説明
1,2,6,24,120,…
次の数、分かりますか?
次の数は、720です。
どんなルールになっているでしょう?
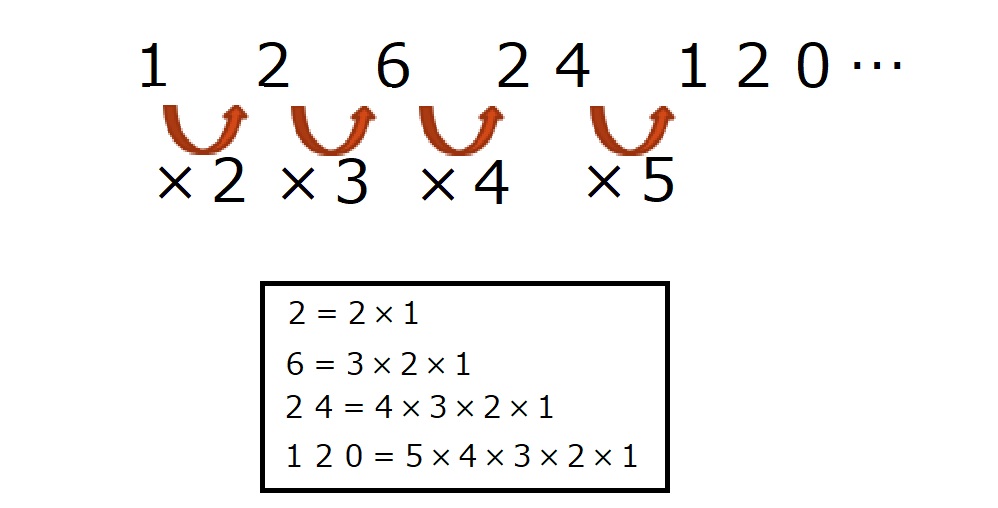
ひたすら掛け算を増やしていっているわけです。
でも掛け算をかきまくるのは長くて大変。
こういった数を表す記号が欲しくなり、
$n!=n×(n-1)×(n-2)×\cdots ×2×1$
と定めたものが階乗のはじまりです。
(定義)
$1$から$n$までの自然数を全てかけ合わせたものを、
$n$の階乗といい、
$n!=n×(n-1)×(n-2)×\cdots ×2×1$
で表す
さて、今までは、
1,2,6,24,120,…
という数の並びを右向きに見ていました。
これを逆向きに眺めていきましょう。
すると、1!の左隣に0!がありそうです。
では、0!はどんな値をとるでしょうか?
今までの規則性を逆に眺めてみましょう
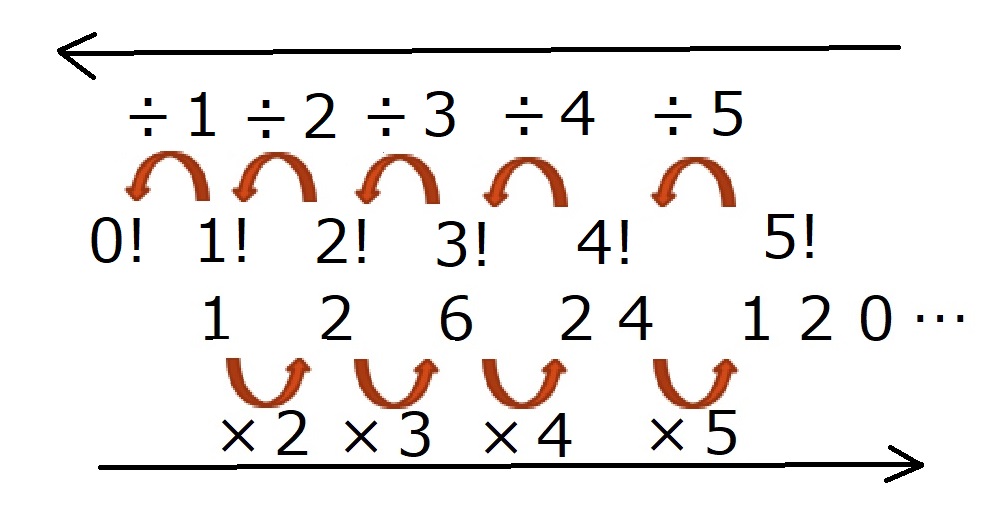
4!=5!÷5
3!=4!÷4
2!=3!÷3
1!=2!÷2
ということは、
0!=1!÷1なのでは?
0!=1っぽい!!!
以上。
なぜ0!=1となるのか?
その理由の一つは
1!=1,2!=2,3!=6,4!=24,5!=120,…
と、階乗の数を並べ、それを逆向きに眺めると、
必然的に0!=1となるからです。
規則性に基づくとそうならざる負えない、というのが理由①です。
次に他の見方も紹介します。
組み合わせによる説明
組み合わせによる説明をする際には、新たな記号が2つ必要になります。
①順列の公式 ${}_n \mathrm{P}_k$
②組み合わせの公式 ${}_n \mathrm{C}_k$
以上2つです。
①順列の公式 ${}_n \mathrm{P}_k$について
例えばこんな問題を考えてみましょう
(問題)
A,B,C,Dの4人を横一列に並べる方法は、何通りあるか
解答
4人並べるので、4つのスペースを確保しておきます。
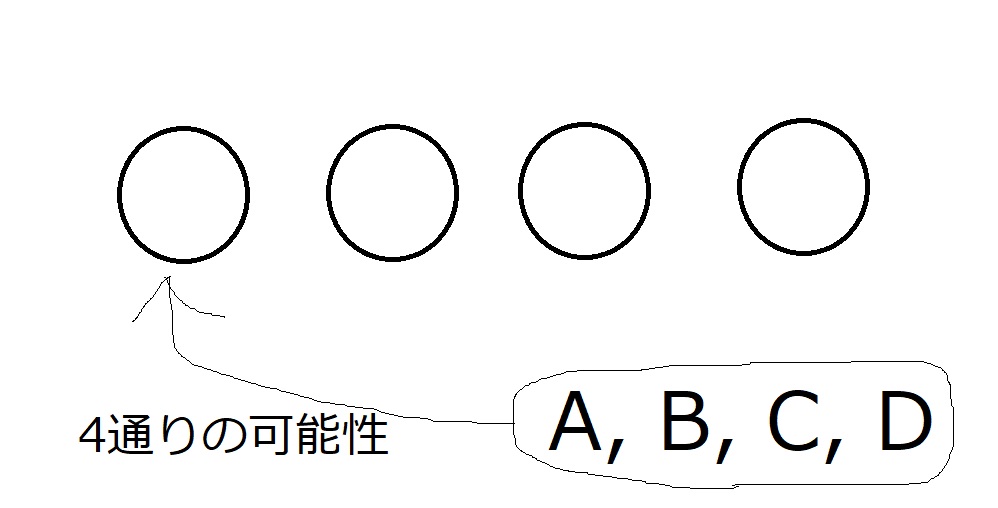
一つ目のスペースには、A,B,C,Dの4人誰が並んでもOKなので、4通り入り方があります。
例えば、Aが最初のスペースに入ったとしましょう
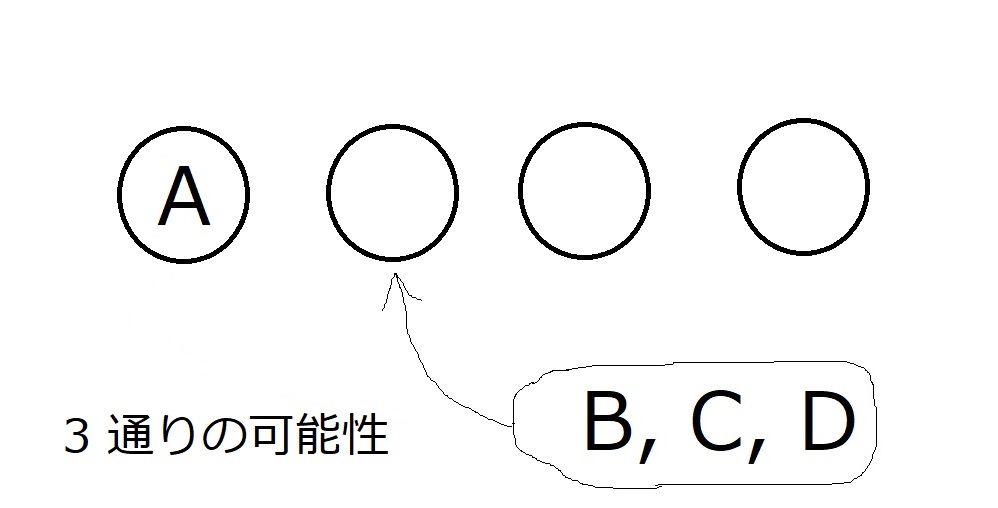
すると、2つ目のスペースに並べるのは、B,C,D の3人のみです。3通り
以下同様に、3つ目のスペースに並べるのは2通りで、4つ目のスペースに並べるのは1通りです。
これらのことから、求める答えは
5×4×3×2×1=120(通り)となります。
5!=120(通り)でもよいです。
さて、ではこんな問題はどうでしょう?
(問題)
A,B,C, Dの4人から2人選んで横1列に並べる方法は何通りか?
解答
先ほどの作業を途中で止めればOKです
2人並べるので、2つ場所を作ります。
最初のスペースに並べるのはA,B,C,Dの4人。すなわち4通りです。
最初のスペースにはAが座ったとしましょう。
次のスペースに座れるのはB, C, D の3人ですすなわち3通り。
よって求める答えは、4×3=12(通り)です。
4人から2選んで並べる、というのを数式で表したくなり、記号を与えたのが
${}_4 \mathrm{P}_2$です。
すなわち、
${}_4 \mathrm{P}_2=4×3=12$
です。
7人の中から3人選んで並べる
なら、
${}_7 \mathrm{P}_3=7×6×5=210$(通り)
です。
②組み合わせの公式${}_n \mathrm{C}_k$について
組み合わせを考える際には、次の2つの問題を比べてみると分かりやすいです。
(問題)
A, B, C, D, E, Fの6人から2人選んで横一列に並べる。
並べ方は何通りか。
さっきと同じで、
${}_6 \mathrm{P}_2=6×5=30$(通り)
となります。大切なのはここから。
この問題を考える際、ABとBAは、別の並び方ですよね。
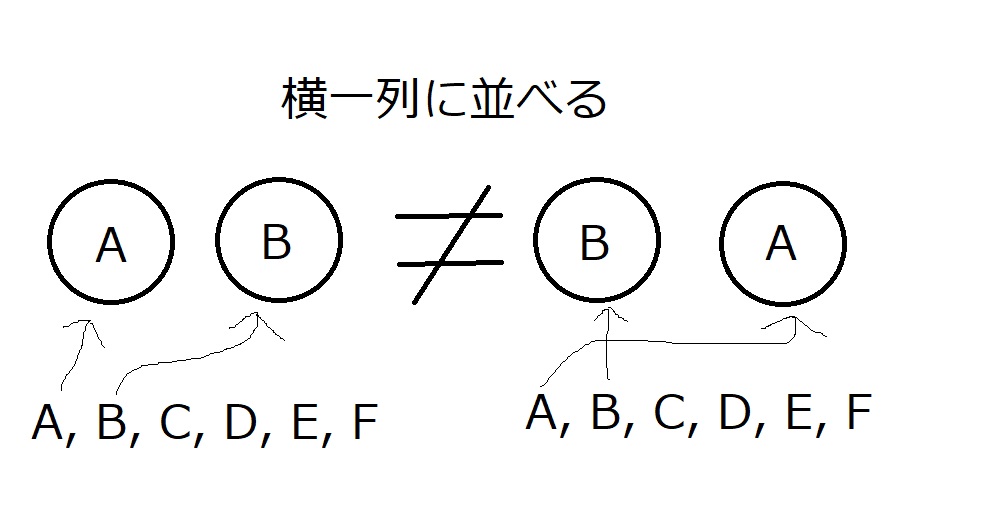
これだけ押さえておいてください。
次の問題に行きましょう
(問題)
A, B, C, D, E, Fの6人から2人選んでグループを作るやり方は何通りあるか
はい。さっきの問題とほぼ同じ分ですが、数学的にはちょっと異なります
なにが異なるか分かりますか?
この問題では
AB とBA は、同じグループとみなさなければなりません。
だってグループ分けするだけですから。順番は関係ないのです。
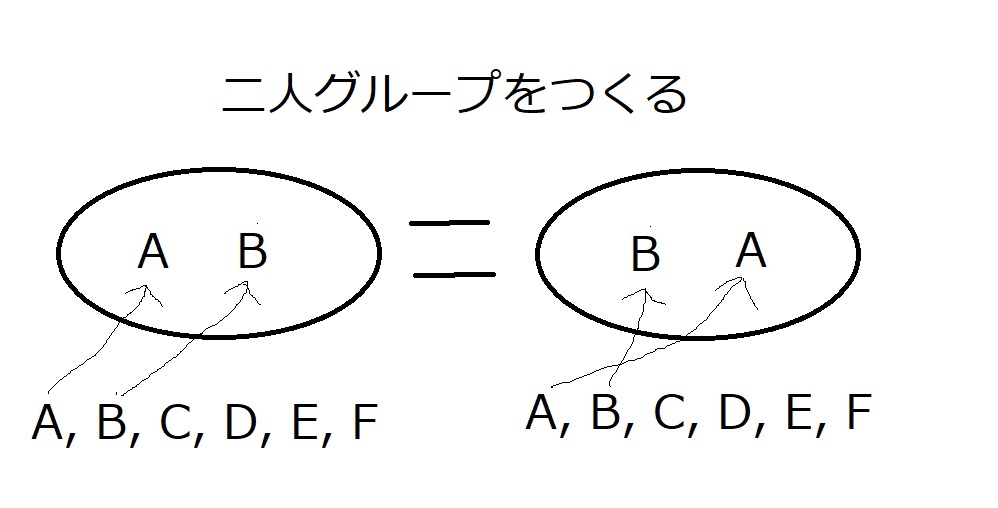
この問題では、
${}_6 \mathrm{P}_2=6×5$
という式だと多すぎます。
ABとBAのようなものを別々のものとしてカウントしているからです。
しかし今回はABとBAは同じものとして扱わないといけません。
A, B2つの慣れべ替えは、2!通りあるので、
6×5を2!で割る必要があります。
よって、この問題で求める数は、
$\dfrac{6×5}{2!}=15$(通り)
となります。
$\dfrac{6×5}{2!}$も記号が割り振られています。
$\dfrac{6×5}{2!}={}_6 \mathrm{C}_2$
と表します。
ここで、$\dfrac{6×5}{2!}$に着目します。
分母は階乗で表されていますが、分子はそうではありません。
分母・分子、両方階乗で表したい!
という要望があり、ちょっと回りくどいですが
$\dfrac{6×5}{2!}$
を変形します。
分母の6×5を6!にするには、4×3×2×1が必要です。
そこで、分子分母に4×3×2×1をかけます。
$\dfrac{6×5}{2!}=\dfrac{6×5×4×3×2×1}{2!×4×3×2×1}=\dfrac{6!}{2!4!}$
となります。
つまり、
${}_6 \mathrm{P}_2=\dfrac{6!}{2!4!}$
です。
ここで、さらに注目すべき点があります。
分母に注目しましょう。
$2!4!$
となっていますが、2+4=6です。
ちょっとすごくないですか?
2+4=6をちょっと変形します
4=6-2です。
これを、4!に代入すると、
4!=(6-2)!となります。
よって、
${}_6 \mathrm{C}_2=\dfrac{6!}{2!4!}=\dfrac{6!}{2!(6-2)!}$
です!あとは、6をn、2をrに置き換えると、、公式完成です。
${}_n \mathrm{C}_r=\dfrac{n!}{r!(n-r)!}$
です。
さぁ、$0!=1$を説明する準備が整いました。
この公式を使って次の問題を問題を考えてみましょう。
A,B,C,D の4人から、4人を選んでグループを作る方法を求めよ
こんなもんは、ABCDの1通りに決まっていますが、あえてさっきの公式を使うと、
${}_4 \mathrm{C}_4=\dfrac{4!}{4!(4-4)!}=\dfrac{1}{0!}$
となります。ここで、${}_4\mathrm{C}_4=1$であって欲しいので、
$\dfrac{1}{0!}=1$でなければなりません。
よって、$0!=1$と定義すると都合がよいです。
要するに、$0!=1$
と定める理由の2つ目は、
${}_4\mathrm{C}_4=1$を成立させたいから、
という整合性による要求だったわけです
他にも、大学数学でマクローリン展開という道具をゲットすると、
また違った見え方がするのですが、
それは別の機会に紹介しようと思います。
ご期待ください。
まとめ
今回は、0!=1と定める理由を2つ紹介しました
理由① 階乗の数を並べて逆向きに眺めたときの規則性から定まる
理由② ${}_4 \mathrm{C}_4=1$という式を成立させるための整合性の要求から定まる
以上!
また次回の記事でお会いしましょう

コメント