$(x+y)^2=x^2+2xy+y^2$
言わずと知れた二乗の展開公式です。
中学3年生で出会い、入試でめっちゃ使ったことでしょう。
そすて、高校2年生になると、数学Ⅱで三乗の展開公式
$(x+y)^3=x^3+3x^2y+3xy^2+y^3$
とならいます。
ここまできたら、当然
$(x+y)^4$や$(x+y)^5$
の展開項も欲しくなってくるのが、数学ジャンキーです。
パスカルの三角形
突然ですが、今から僕がある規則性に基づいて数を並べていくので、
続きを考えてみてください。
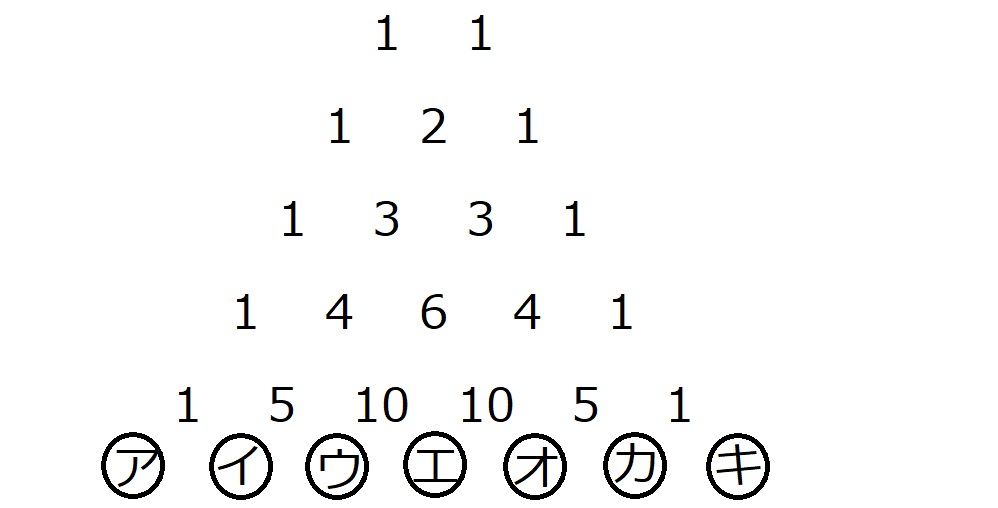
最後の段のに㋐㋑㋒㋓㋔㋕㋖に入る数字はどうなるでしょう?
正解は、こうです。
㋐, ㋑, ㋒, ㋓, ㋔, ㋕, ㋖ =1,6,15,20,15,6,1
今回の三角形っぽい並べ方は、
隣り合う数字の和が下段の数になる
というルールに支配されていたのです!
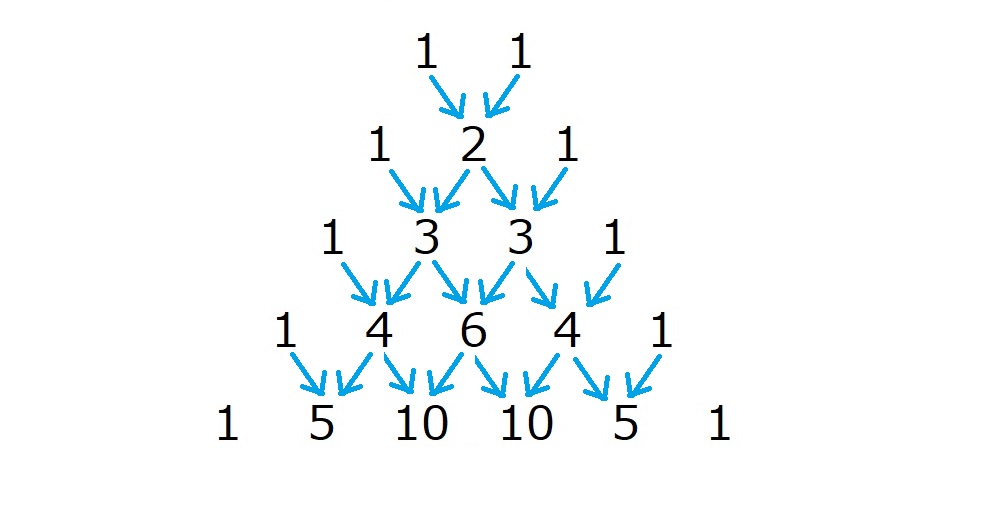
このルールで三角形上にならんだ数を、
パスカルの三角形
といいます。
2乗の展開公式の一般化へ向けて
ある公式を一般化して新しい定理をゲットしたい。
こんなとき。
何から始めますか?
そう。
研究の第一歩は、いつだって観察です。
具体例をひたすら並べていきます。
$(x+y)^1=x+y$
$(x+y)^2=x^2+2xy+y^2$
$(x+y)^3=x^3+3x^2y+3xy^2+y^3$
$(x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4$
なんか、すごくとてつもない神秘を感じませんか?
なんと、
係数がパスカル三角形と一致しているのです!!!
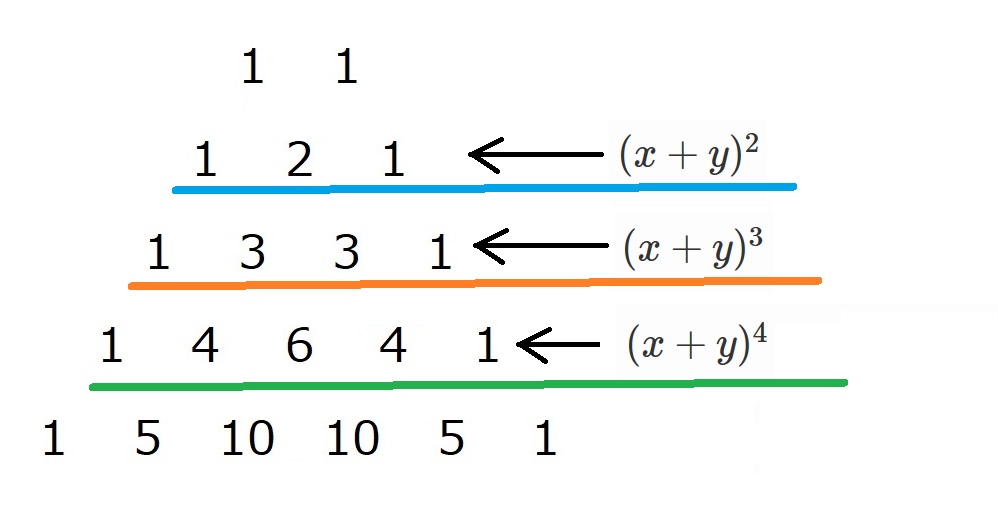
ヤバくないですか?
ヤバいですよね?
ヤバいと思ってください(圧)
つまり、$(x+y)^{5}$
を計算してください、と言われたら、
$x^5, x^4y, x^3y^2, x^2 y^3, xy^4, y^5$
を並べて、
パスカル三角形を5段階かいて、
一番下の数たちを係数にすれば、
$(x+y)^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5$
それで完成なのです!
なんということでしょう!
あのめんどくさい展開作業を一切しなくていいのです。
革命的です。
しばらくこの感動に酔いしれましょう!
組み合わせの三角形
さて、先ほどは
$(x+y)^n$
の展開公式に現れる係数と、パスカル三角形が一致しているという真に驚嘆すべき事実を知りました。
これによって、めんどくさい展開の計算を実行しなくても、上から順番にパスカル三角形をかけば
それを係数として公式を完成させることができます。
これは革命的です。
が、しかし。
例えば$(x+y)^{100}$の係数はどうなる?
とか言われると、パスカル三角形を100段かくことになり、日が暮れます。
うわぁぁぁ!そんな!
百乗を展開するよりましではあるものの、結局は脳筋手計算で頑張るしかないのか!?
そんなことはありません。
先ほどの話には続きがあるのです。
組み合わせの式${}_nC_r$を用いて以下のように三角形を作っていきます
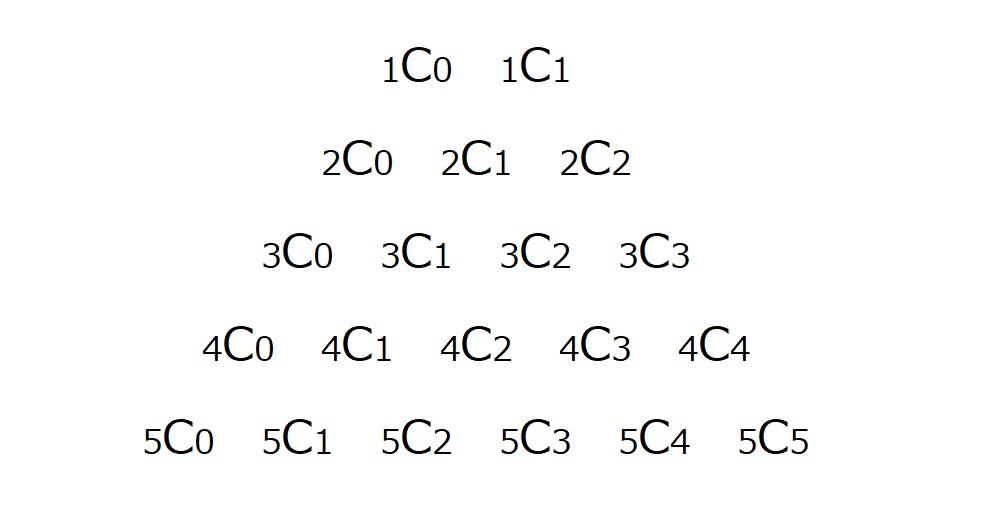
さて
これを見て、何かに気づきませんか?
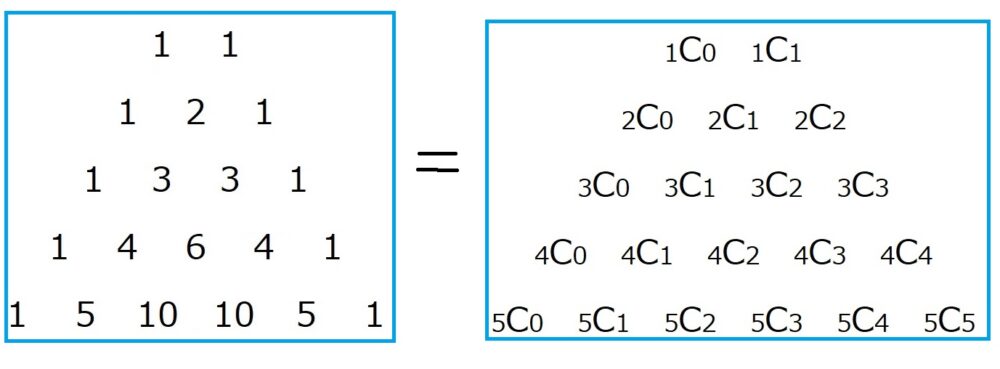
パスカル三角形と一致するのです!!
マジで!? 超便利じゃん!!
そう。
これ、超便利なんです。
何が便利なのか?
それはパスカル三角形と比較すると分かります。
先ほど確認した通り、パスカル三角形の場合は、
100段目の数はどうなってますか?
と聞かれた場合、上から足し算していかなければ分かりません。
しかし、組み合わせの三角形は、100段目のすうはどうなってますか?
と言われたとき、
あぁ、100段目ね。
なら${}_{100}\mathrm{C}_0$から始めればいいぜ!
${}_{100}\mathrm{C}_0, {}_{100}\mathrm{C}_1, {}_{100}\mathrm{C}_2, \cdots, {}_{100}\mathrm{C}_{100}$
と、すぐに分かります。
よって、
$(x+y)^{100}={}_{100}\mathrm{C}_0 x^{100}+{}_{100}\mathrm{C}_1 x^{99}y+{}_{100}\mathrm{C}_1 x^{98}y^2+\cdots +{}_{100}\mathrm{C}_{100}y^{100} $
となり、百乗の展開公式を得ることができます。
そして、さっきの$100$を$n$に置き換えると、
$(x+y)^n$の展開公式を得ることができます。
$(x+y)^{n}={}_{n}\mathrm{C}_0 x^{n}+{}_{n}\mathrm{C}_1 x^{n-1}y+{}_{n}\mathrm{C}_1 x^{n-2}y^2 +\cdots +{}_{n}\mathrm{C}_{n}y^{n} $
いわゆる二項定理と呼ばれるものです
$(x+y)^n$の係数と、${}_n\mathrm{C}_r$を並べてできる三角形(パスカル三角形)が一致するという
衝撃の事実から得られる公式。
それが二項定理なのです。
さて。
じゃ、なんでこんな神秘的なことが成り立つの?
なんで$(x+y)^n$の係数に${}_n\mathrm C_r$が登場するの?
という点について説明していこうと思います。
理屈の説明
定理・公式を証明したり、理解したりする際に初めにすることは、
いつだって具体例の観察です。
今回も$(x+y)^n$の$n$の値を具体的に定めて観察をしていきましょう。
まずは$n=2$の場合からです。
$(x+y)^2=(x+y)(x+y)$ですね。
これを展開するわけですが、その際に色分けをしておくと分かりやすいので、青とオレンジを使います。
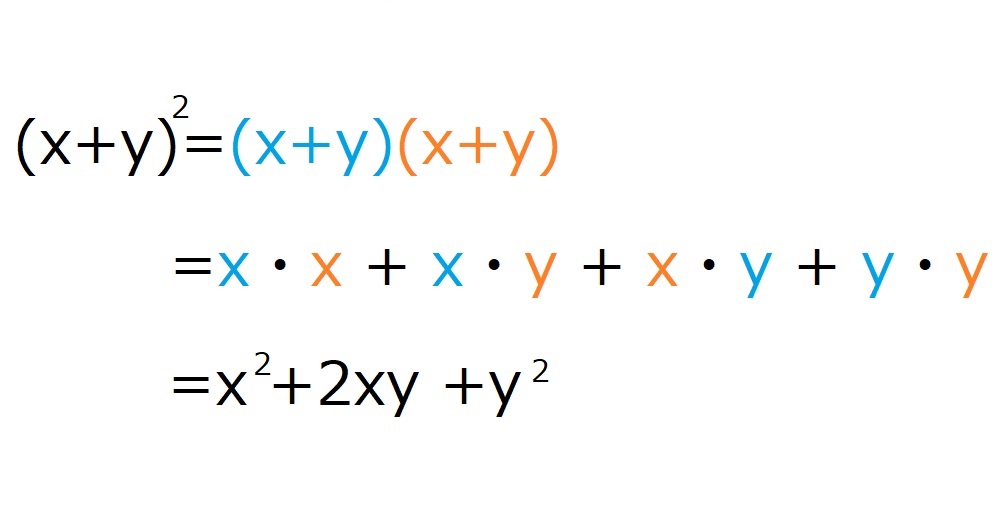
$(x+y)^2$を展開する際の$xy$について考えてみましょう。
$xy$をつくるには、当然のことながら、$x$が1個、$y$が1個必要です。
いま、$x$は青いやつとオレンジのやつがあります。$y$も同様です。
ゆえに、青い$x$とオレンジの$y$でつくる$xy$と、
オレンジの$x$と青い$y$でつくる$xy$が存在します。
$xy$の作り方が2通りなので、$xy$の係数は2なのです。
この調子で$n=3$の場合を考えてみましょう。
色は三色にします。青と、オレンジと、緑です。
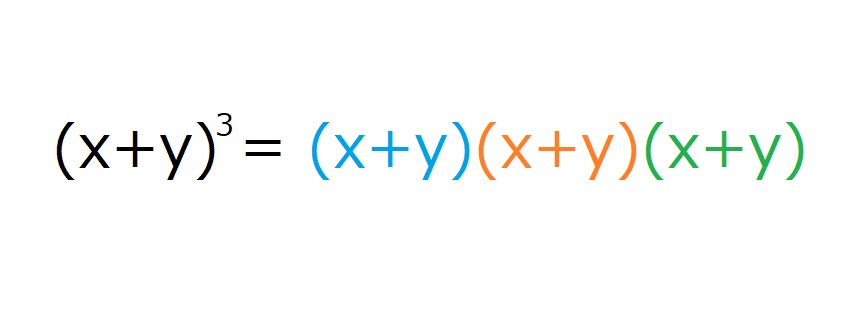
例えば、$x^2y$について考えてみましょう。
$x^2y$をつくるには、$x$が2個と$y$が1個必要です。
$x$は青いやつ、オレンジのやつ、緑のやつがあります。
これら3種類の$x$から、2個$x$を選んで取ってきます。
この選び方は、${}_3\mathrm{C}_2$通りです。
(ちなみに、$x$を確定させると、$y$は自動的に残っている色から選ぶことになります)
ゆえに、$x^2y$のつくりかたは${}_3\mathrm{C}_2$通りとなり、
$x^2y$の係数は${}_3\mathrm{C}_2$となるのです!
同じように、
$(x+y)^{100}$について、
$x^{98}y^2$の係数を考えると、
100種類の$x$から98個選ぶことになり、$y$は自動的に残っている色から選ぶことになるので、
この選び方は${}_{100}\mathrm{C}_{98}$となるわけです。
こうして、
$(x+y)^n$の展開公式の係数には組み合わせの式${}_n\mathrm{C}_r$が登場することになり、
これを並べてかいたのが二項定理の正体だったのです。
ちなみに、${}_n\mathrm{C}_r$は二項定理の係数となることから、
二項係数とも呼ばれます。
まとめ
いかがでしたか?
・パスカル三角形ヤバい!
・パスカル三角形と${}_n\mathrm{C}_r$を並べた三角形は一致する
・$(x+y)^n$の展開公式には${}_n\mathrm{C}_r$が登場する
・展開公式を二項定理という
二項定理はめっちゃすごい定理で、いろんな場面で活躍します。
ご期待ください。
公式lineで受験に関する無料相談を実施してますので、
よければ友達追加してください↓
ではまた次回の記事でお会いしましょう!
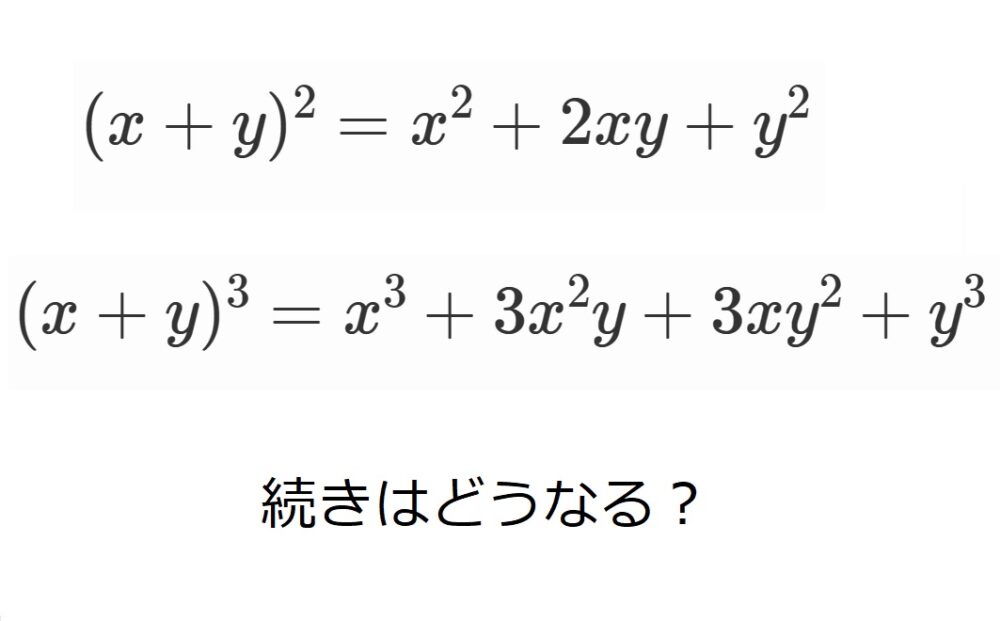
コメント
コメント一覧 (6件)
つまり、(x+y)^5を計算してください…
に続く指数の並びが一部ずれているかと思います。
確認お願いします。
57は素数さん
コメントありがとうございます
カンマの位置がおかしいですね
ご指摘ありがとうございます
修正いたしました
大変助かります
ありがとうございました
めっちゃわかりやすかったですありがとうございます
中学3年生さん
嬉しいコメントありがとうございます。
当ブログの記事が学びの役に立てたのなら幸甚です。
ぜひ今後も勉学に励んでください
応援しております!
つまり、(x+y)5を計算してください、と言われたら、【x5,x4y,x3y2,x2y3,xy4,y4】を並べて…
とあるのですが、その並べたもの【】内の文字式(?)はどこからどうやって出てきたんですか?
それが分からないのでその先も分からないです…
どうやって出すのか考えようとすると結局展開して考えるしかないので、パスカルの三角形を使うことができないです
数学アレルギー40代母さん
ご質問ありがとうございます。
【x5,x4y,x3y2,x2y3,xy4,y5】の部分は(x+y)^5単品で思いつくというよりも、
それより前の(x+y)^2や(x+y)^3や(x+y)^4の展開結果の観察から規則性に気づいていきましょう、
といった意図で書きました。
当方の打ち間違いで最後の部分がy^5ではなくy^4と表記されていたので混乱させてしまったかもしれません。
その点は申し訳ありません。ただいま修正しましたので再度ご確認ください。
さて、ご質問いただいた点について返信いたします。
係数は考えずに文字の部分だけみとると、
(x+y)^2は【x^2, xy, y^2】が登場し、これにパスカル三角形を係数として付けたものになっています。
(x+y)^3は【x^3, x^2y, xy^2, y^3】が登場しこれにパスカル三角形を係数として付けたものになっています。
例えばxに着目すると、いずれも最高次から一つずつ次数が下がっていくように配置されており、
yは逆に次数がひとつづつ上がっていくように配置されていることが分かります。
実際、
(x+y)^4は【x^4, x^3y, x^2y^2, xy^3, y^4】が登場しますね
これらの観察結果から見つけた規則性に従うと、
(x+y)^5は【x^5, x^4y, x^3y^2, x^2y^3, xy^4, y^5】が登場するだろうと予測できる、
といった意図です。
ぜひ観察結果から規則性を見出すといった視点で数学を楽しんでいただければと思います。