ユークリッドの互除法ってガロア理論と関係あるの?
ユークリッドの互除法は、2つの整数の最大公約数を求めるための道具です。
詳しくはこちらを参照
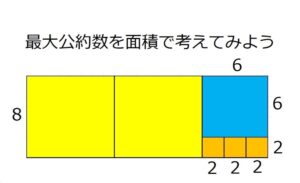
そして、ガロア理論は、方程式についての理論です。
詳しくはこちらを参照


両者は一見すると全く関係がないように思えますが、
実は密接に関わっています。
ユークリッドの互除法は、2つの整数の最大公約数を求める道具。
つまりは約数を求めるわけです。
「約数を求める」ということを、「数を掛け算に分解する」というイメージでとらえてください。
$6=2×3$
のイメージです。(これは約数を求めるというより素因数分解ですが)
一方、ガロア理論は方程式についての理論です。
さて皆さん、方程式を解くときは何をしますか?
例えば、$x^2-5x+6=0$を解いてみましょう。
$x^2-5x-6=(x-2)(x-3)$
$(x-2)(x-3)=0$より、
$x=2, 3$
因数分解をしましたね!
因数分解ができないときは、解の公式を使いますが、第一の選択肢は因数分解のはずです。
そして、因数分解は、「多項式を掛け算に分解する」道具です。
以上をまとめると、こうなります。
ユークリッドの互除法→数を掛け算に分解する道具
方程式を解く→因数分解→多項式を掛け算に分解する道具
どうでしょうか?
ユークリッドの互除法と、ガロア理論(方程式の因数分解)が、
「掛け算への分解」という点で同じような属性であるような実感がわきませんか?
昔の人は、この実感を基にして、
多項式にユークリッドの互除法を使ってみる
という最高にエキサイティングなことを思いつきます。
今回はこの手法について扱っていきます。
ユークリッドの互除法多項式Ver
例えば、$x^5-x^4+2x^2-2x+1$と$x^4-x^3-x^2+2x-2$を考えてみましょう。
この2つの多項式の約数を求めてみます。
2つとも、そのまま因数分解するのは難しそうなので、ユークリッドの互除法を用います。
$x^5-x^4+2x^2-2x+1=(x^4-x^3-x^2+2x-2)×x+(x^3+1)$
$x^4-x^3-x^2+2x-2=(x^3+1)(x-1)+(-x^2+x-1)$
$x^3+1=(-x^2+x-1)(-x-1)+0$
これでユークリッドの互除法は完了です。
しかし最後の式が若干みにくいので、係数だけ調整します。
$x^3+1=(-x^2+x-1)(-x-1)+0$より、
$x^3+1=(x^2-x+1)(x-1)$
よって、今回の2つの多項式の約数は$x^2-x+1$となります。
このように、2つの多項式の約数を整数の時と同じようにユークリッドの互除法で求めることがでるのです!
ここで少しだけ注意が必要です。
多項式を因数分解する際は、
係数の範囲をどこで考えているかがめっちゃ重要です。
$x^2-2$は係数が有理数の範囲では既約ですが、実数の範囲では可約になります。
多くの場合は、係数の範囲を有理数で考えると都合がいいので、
この記事でもそう考えていこうと思います。
(中学・高校では、暗黙のうちに係数の範囲を整数に限定していることが多い気がするので、注意してください。もし中高生の読者の方がいたとしたら、テストでは学校で習った通りに因数分解しましょう。ただ、ガロア理論では、体が非常に重要な役割を果たすので、最小の体である有理数を係数として出発するのが一番自然です。係数を有理数で考えるのは、中高生には若干違和感があるかもしれませんが、慣れていきましょう)
係数の範囲が有理数ということは、こんな現象がおきます。
$x^2-9$を例に考えましょう
もちろん$x^2-9=(x+3)(x-3)$ですので、
$x+3とx-3$は$x^2-9$の約数です。
しかし、係数の範囲は有理数なので、例えば
$x^2-9=(2x+6)(\dfrac{1}{2}x-\dfrac{3}{2})$と因数分解してもよいことになります。
このとき、$2x+6と\dfrac{1}{2}x-\dfrac{3}{2}$も$x^2-9$の約数だね、といっても間違いではありません。
要するに、係数が有理数の範囲で因数分解をする場合は、有理数倍は無視して、同じものとみなします。
$x+3も2x+6も\dfrac{1}{100}x+\dfrac{3}{100}も$、$a(x+3)$という形なので、どれもが$x^2-9$の約数です。
普通は最高次の係数が1であるものがシンプルなので、$a(x+3)$の$a$は省略することが多いです。
=====================
割り算の詳細が気になる方は、以下のひっ算を参考にしてください(ここは読み飛ばしても全然OKです)
$x^5-x^4+2x^2-2x+1$と$x^4-x^3-x^2+2x-2$を割り算します。
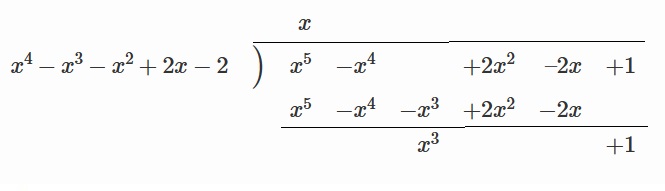
$x^5-x^4+2x^2-2x+1=(x^4-x^3-x^2+2x-2)×x+(x^3+1)$
同じノリで、$x^4-x^3-x^2+2x-2$を$x^3+1$で割ります。
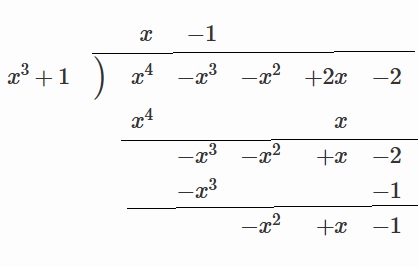
式にすると、こうです
$x^4-x^3-x^2+2x-2=(x^3+1)×(x-1)+(-x^2+x-1)$
さらに、同じノリで$x^3+1$を$-x^2+x-1$で割ります。
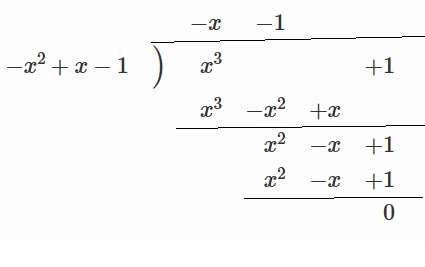
式を追うと複雑ですが、伝えたいことはただ一つです。
多項式にもユークリッドの互除法が使え、
共通因数を求めることができる。
この事実だけ覚えておいてください。
ユークリッドの互除法と1次不定方程式
さて、ユークリッドの互除法の次に出てくる話題として、1次不定方程式があります。
詳しくはこちらを参照

$2 つの整数 a, b$が互いに素なとき、$ax+by=c$は整数解をもつ、といった内容です。
これ、$a, b$を多項式に置き換えても同じようなことが成り立ちます。
$2つの多項式a(x), b(x)$が互いに素であるとき、$a(x)X(x)+b(x)Y(x)=1$となるような$X(x), Y(x)$が存在し、$Y(x)がa(x)$の次数よりも低くなる、といった感じです。
具体例を見ていきましょう。
まずは、2つの多項式が互いに素って何?どういうこと?と思ったに違いないので、そこから確認します。
整数の場合は、最大公約数が1のときに互いに素と言いました。
たとえば、2と9は互いに素です。4と6は互いに素ではありません
多項式の置き換えるとどうでしょうか。
例えば、$x^2-9$と$x^2-5x+6$を考えましょう。
$x^2-9=(x+3)(x-3)$で、$x^2-5x+6=(x-2)(x-3)$です。
$x-3$が両者に共通なので、これらは互いに素ではありません。
$x^2-9=(x+3)(x-3)$と$x^2-x-2=(x-2)(x+1)$は互いに素です。
問
$(x^3-1)X(x)+(x^2-x-2)Y(x)=1$となる有理数係数の多項式$X(x), Y(x)$の組を1つ求めよ
注意:結構計算がえぐいので、なんとなく目で追っていただければOKです。
気が向いたら筆算しつつ計算もしてみてください。
解答
$x^3-1=(x^2-x-2)(x+1)+3x+1\cdots ①$
$x^2-x-2=(3x-1)(\dfrac{1}{3}x-\dfrac{4}{9})-\dfrac{14}{9}\cdots②$
②より、$-\dfrac{14}{9}=(x^2-x-2)-(3x-1)(\dfrac{1}{3}x-\dfrac{4}{9})\cdots ②’$
①より、$3x+1=(x^3-1)-(x^2-x-2)(x+1)\cdots ①’$
②’に①’を代入
$-\dfrac{14}{9}=(x^2-x-2)-\lbrace (x^3-1)-(x^2-x-2)(x+1) \rbrace×(\dfrac{1}{3}x-\dfrac{4}{9})$
$-\dfrac{14}{9}=(x^2-x-2)-(x^3-1)(\dfrac{1}{3}x-\dfrac{4}{9})+(x^2-x-2)(x+1)(\dfrac{1}{3}-\dfrac{4}{9})$
$-\dfrac{14}{9}=(x^2-x-2)(\dfrac{1}{3}x^2-\dfrac{1}{9}x+\dfrac{5}{9})-(x^3-1)(\dfrac{1}{3}x-\dfrac{4}{9})$
全体を$-\dfrac{9}{14}$倍する。
$1=(x^2-x-2)(-\dfrac{3}{14}x^2+\dfrac{1}{14}x-\dfrac{5}{14})-(x^3-1)(-\dfrac{3}{14}x+\dfrac{2}{7})$
よって、$(x^3-1)(\dfrac{3}{14}x-\dfrac{2}{7})+(x^2-x-2)(-\dfrac{3}{14}x^2+\dfrac{1}{14}x-\dfrac{5}{14})=1$
となり、$X(x)=\dfrac{3}{14}x-\dfrac{2}{7}, Y(x)=-\dfrac{3}{14}x^2+\dfrac{1}{14}x-\dfrac{5}{14}$は求めるものの一組となる。
解答終了
まとめ
いかがでしたか?
計算がやばかったと思いますが、要点をまとめると以下の3点です。
これだけ知っておいていただければ、この記事を書いたかいがあります。
・多項式でもユークリッドの互除法が使える。
・1次不定式方程式$ax+by=c$の多項式バージョンも考えることができる
・$a(x), b(x)$が互いに素なとき、$a(x)X(x)+b(x)Y(x)=1$となる$X(x), Y(x)$の組が存在し、$a(x)$の次数より$Y(x)$の次数の方が低くできる
ここまで読んでいただきありがとうございます!

コメント