2次方程式の解と係数の関係
今回は、解と係数の関係について扱っていきます。
ふつう、方程式について考えるときは、まず方程式が与えられて、それを解いて解を求めます。
例えば、
$x^2-5x+6=0$が先に与えられます。
そして、これを解きます。
$(x-2)(x-3)=0$より、
$x=2, 3$といった感じです。
図にすると、こんな感じです。

解と係数の関係は、この逆のステップをたどります。
先に解が与えられて、それをベースに方程式をつくります。
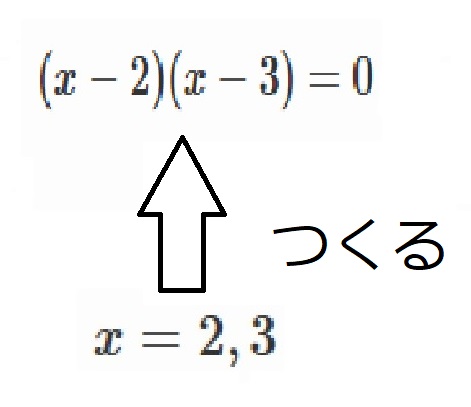
例えば、$x^2+ax+b=0$の解
$x=\alpha$と$x=\beta$が先に与えられたとします。
これを解にもつ方程式は、
$(x-\alpha)(x-\beta)=0$が考えられます。
ちょっと難しい言葉を使うなら、この方程式を得る過程で因数定理を使っています。
この方程式を有理数倍した$p(x-\alpha)(x-\beta)=0$
でもいいですが、数学はシンプルを好むので、$p=1$として
$(x-\alpha)(x-\beta)=0$を考えましょう。
展開して整理すると、
$x^2-(\alpha + \beta)x+\alpha \beta=0$
となります。これと$x^2+ax+b=0$を係数比較しましょう。
$\alpha + \beta =-a, \alpha \beta =b$
となります。これが解と係数の関係です。
今回は$x^2$の係数が1である方程式$x^2+ax+b=0$の解と係数の関係を紹介しましたが、
一般の$ax^2+bx+c=0$の場合もほぼ同じやり方で導けますので、セットで確認します。
$ax^2+bx+c=0$の全体を$a$で割ります。
$x^2+\dfrac{b}{a}x +\dfrac{c}{a}=0$
これの解を$x=\alpha, \beta$とします。
$x=\alpha, \beta$を解にもつ方程式としては、例えば
$(x-\alpha)(x-\beta)=0$があります。
($x^2$の係数が1であるものをチョイスしています)
展開すると、
$x^2-(\alpha + \beta)x+\alpha \beta=0$
$x^2+\dfrac{b}{a}x +\dfrac{c}{a}=0$と係数比較すると、
$\alpha +\beta =-\dfrac{b}{a}, \alpha \beta =\dfrac{c}{a}$
これが一般の場合の解と係数の関係です。
大学入試のテクニックとしては、解と係数の関係は方程式を作るときにつかいます。(そこから実数条件につなげる)
具体的には、
$\alpha +\beta =〇, \alpha \beta =△$のとき、
$\alpha, \beta$は二次方程式$t^2-〇 t+△=0$の解である、といった具合で使います。
ともかく、これで2次方程式の解と係数の関係を得ることができました。
では、研究者の目で今のことを眺めてください。
次に何をしたくなりますか?
3次方程式の解と係数の関係
2次方程式に解と係数の関係があるなら、当然3次方程式にも解と係数の関係はありそうです。
同じようなやり方で、3次方程式の解と係数の関係を導いてみましょう。
$ax^2 +bx^2 +cx +d=0$を考えます。
今回は初めから最高次の係数が1でない場合を考えます。
$ax^2 +bx^2 +cx +d=0$
の全体を$a$で割ります。
$x^3+\dfrac{b}{a}x^2+\dfrac{c}{a}x +\dfrac{d}{a}=0$
ここで、この方程式の解が
$x=\alpha, \beta, \gamma$
と与えられたとします。
これらを解に持つ方程式としては、
$(x-\alpha)(x-\beta)(x-\gamma)=0$
が考えられます。展開して整理すると、
$x^3-(\alpha +\beta +\gamma)x^2+(\alpha \beta +\beta \gamma +\gamma \alpha)x -\alpha \beta \gamma=0$
となります。
$x^3+\dfrac{b}{a}x^2+\dfrac{c}{a}x +\dfrac{d}{a}=0$
と係数比較をすると、
$\alpha +\beta +\gamma =-\dfrac{b}{a}$
$\alpha \beta +\beta \gamma +\gamma \alpha =\dfrac{c}{a}$
$\alpha \beta \gamma =-\dfrac{c}{a}$
となります。
これが3次方程式の解と係数の関係です。
次に何をしたくなりますか?
具体例を観察したら、規則性に注目!です。
これらの結果を基に、4次方程式の場合を予想してみませんか?
4次方程式の解と係数の関係
2次方程式$ax^2+bx+c=0$の解と係数の関係
→$\alpha +\beta =-\dfrac{b}{a}, $
$\alpha \beta =\dfrac{c}{a}$
3次方程式$ax^3+bx^2+cx+d=0$の解と係数の関係
→$\alpha +\beta +\gamma=\dfrac{b}{a},$
$ \alpha \beta +\beta \gamma +\gamma \alpha =\dfrac{b}{a}, $
$\alpha \beta \gamma =-\dfrac{c}{a}$
さぁ準備は整いました。
4次方程式$ax^4+bx^3+cx^2+dc+e=0$の場合を予想しましょう。
2次方程式の場合は、関係式は2つです。
3次方程式の場合は、関係式は3つです。
おそらく4次法廷s気の場合は、関係式4つでしょう。
符号は、1つ目の関係式がマイナスで、次はプラス、次はマイナス、と交互になるようです。
つぎは次数に着目しましょう。
3次方程式について考えると、
一つ目の関係式$\alpha +\beta +\gamma$は次数1で3項の式です。
二つ目の関係式$\alpha \beta +\beta \gamma +\gamma \alpha$は、次数2で3項の式です。
3つ目の関係式$\alpha \beta \gamma$は次数3の単項式です。
これらのことから、解と係数の関係の式は、少しづつ次数が上がっていくと考えられます。
もう少し考えを深めていきましょう。
1つ目の式は、3つの解から1個づつ選んだものの和です。
2つ目の式は、3つの解から2つ筒選んでかけたものの和です。
3つ目の式は、3つの解を全て選んでかけたものです。
これを4次方程式に当てはめてみましょう。
解を$\alpha, \beta, \gamma, \delta$としましょう。
1つ目の関係式は、4つの解から1個づつ選んでかけたものの和。
$\alpha +\beta +\gamma +\delta=-\dfrac{b}{a}$と予想できます。
2つ目の式は、4つの解から2個づつ選んでかけたものの和。
$\alpha \beta +\beta \gamma +\gamma \delta +\delta \alpha=\dfrac{c}{a}$
3つ目の式は、4つの解から3個づつ選んでかけたものの和
$\alpha \beta \gamma +\beta \gamma \delta +\gamma \delta \alpha + \delta \alpha \beta=-\dfrac{d}{a}$
4つ目の式は、4つの解を全てかけたもの
$\alpha \beta \gamma \delta=\dfrac{e}{a}$
と予想できます。
予想を確かめてみましょう。
$(x-\alpha)(x-\beta )(x-\gamma)(x-\delta)$
を展開します。
マジでめんどくさいですが、やってみると
$x^4-(\alpha +\beta +\gamma)x^3$
$+(\alpha \beta +\beta \gamma +\gamma \delta +\delta \alpha+\alpha \gamma + \beta \delta)x^2$
$-(\alpha \beta \gamma +\beta \gamma \delta +\gamma \delta \alpha + \delta \alpha \beta)x$
$+\alpha \beta \gamma \delta$
となりました。
$x^2$のところだけ予想と異なる結果となっています。なぜでしょう?
$x^2$の係数は、予想の通り考えると4つの中から2つ選んだものの積の和なのです。
4つから2つ選ぶので、${}_4 \mathrm{C}_2=\dfrac{4×3}{2×1}=6$
つまり6つの項が出てくるわけです。
$x$の係数が${}_4 \mathrm{C}_3=4$で上手くいったのは偶然だったわけです。
規則性を見つける際にみかけにとらわれすぎるとこういうことが起こりますが、
予想と異なる結果を楽しむのも数学の醍醐味です。
ちなみに、解と係数の関係に出てくる左辺の式を基本対称式といいます。
2次の場合は、$\alpha+\beta, \alpha \beta$が基本対称式となります。
さて。
2次方程式、3次方程式、4次方程式ときました。
次は何をしますか?
n次方程式の解と係数の関係
具体例を観察したら、
一般化してn次方程式を考えたくなるのが数学を愛する者の定めです。
n次方程式の場合は、文字が多くなりすぎるので添え字を活用します。
n次方程式を$a_nx^n +a_{n-1}x^{n-1}+\cdots + a_{1}x +a_0=0$とし、全体を$a_1$で割ります。
$x^n +\dfrac{a_{n-1}}{a_n}x^{n-1}+ \cdots + \dfrac{a_1}{a_n}x+\dfrac{a_0}{a_n}=0$
解を$\beta_1, \beta_2, \beta_3, \cdots, \beta_n$と置きましょう。
$(x-\beta_1)(x-\beta_2)\cdots (x-\beta_n)=0$を展開して整理すると、
$x^n$
$+(-1)(\beta_1 + \beta_2+\cdots +\beta_n)x\\$
$+(-1)^2(\beta_1 \beta_2 +\beta_2 \beta_3+\cdots +\beta_n \beta_1)x^2\\$
$+(-1)^3(\beta_1 \beta_2 \beta_3 +\cdots \beta_{n-1} \beta_{n} \beta_1)x^3 \\$
$+ \cdots\\$
$+(-1)^n \beta_1 \beta_2 \cdots \beta_n$
となり、
$\beta_1 + \beta_2+\cdots +\beta_n =-\dfrac{a_{n-1}}{a_n}$
$\beta_1 \beta_2 +\beta_2 \beta_3+\cdots +\beta_n \beta_1=\dfrac{a_{n-2}}{a_n}$
$\beta_1 \beta_2 \beta_3 +\cdots \beta_{n-1} \beta_{n} \beta_1=(-1)^3\dfrac{a_{n-3}}{a_n}$
$\cdots$
$\beta_1 \beta_2 \cdots \beta_n=(-1)^n\dfrac{a_0}{a_n}$
が導かれます。
これがn次方程式の解と係数の関係です。
まとめ
いかがでしたか?
・因数定理を使って展開と因数分解で解と係数の関係を導く
・解と係数の関係に出てくる式を基本対称式という
・$\alpha +\beta=〇, \alpha \beta =△$のとき、
$\alpha, \beta $は2次方程式$t^2-〇t+△=0$の解となる
・解と係数の関係は一般化できる
以上のことを楽しんでいただけたらと思います。

コメント