二乗してマイナスになる数?
そんなもん、俺は認めねーから!!
と誰もが一度は思うことでしょう。
実は、当時の数学者すらそうでした。
この記事では、虚数単位が数として認められるまでの数学的過程や、その応用、さらにその先の世界について解説します。
高校までで習う数について
我々は、小学1年生で自然数を習います。
リンゴが1個とか、犬が3匹とか、最も素朴な数の概念です。
$\mathbb{N}=\lbrace 1, 2, 3, \cdots, \rbrace$
中学1年生になると負数を習います。
温度が氷点下とか、借金をしたとか、そういう状況を上手く表現できるのが負数です
自然数に負数と0を加えて、整数をゲットします。
$\mathbb{Z} =\lbrace \dots -3, -2, -1, 0, 1, 2, \dots \rbrace$
次の数概念である有理数は、実は小学生の時にほぼ習っています。
1Lのペンキを半分塗ったとか、ケーキを6人で切り分けよう!とか
そういった状況を有理数で表現することができます。
$\mathbb{Q}= \lbrace \dfrac{b}{a} \mid a, b \in \mathbb{Z} \rbrace $
有理数や有理化に興味のある方はこちらの記事をご覧ください

そして、中学3年生で三平方の定理を習って$\sqrt{2}, \sqrt{3}$などをゲットして、
ついでに円周率$\pi$などをスパイスに
実数$\mathbb{R}$を手に入れます。
実数は数直線上にあるすべての数を含んでいます。
人類が実数を手に入れるまでの数学的なプロセスもめっちゃ面白いので、
そのストーリー、人類の英知の結晶、あくなき探究と挫折、そして成功の歴史は、
また別の記事で紹介しようと思います。
今回の主役は虚数単位$i$です。
自然数、整数、有理数、実数と学んできた先に、高校数数学の頂点の一人として君臨するのが
複素数$\mathbb{C}= \lbrace a+bi \mid a, b \in \mathbb{R} \rbrace$です。
今日はこれについて学んでいきましょう!
虚数単位$i$とは?
高校になって数学Ⅱに入ると、$i$という摩訶不思議な数に出会います。
$$i^2=-1$$
え?
二乗してマイナス!?
それありなの?
$i^2=-1$ということは、$i=\sqrt{-1}$ってことになるけど!?
数学Ⅰではルートの中が負になったらダメって習うじゃん!
色々思うところはあると思います。
一応、ルートの中が負でもOKということにすると、メリットがあります。
それは、2次方程式$ax^2+bx+c=0$の解の公式
$x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$
がいつでも使えるようになるからです。
実数までの世界で考えると、
判別式$D=b^2-4ac$
が0以上の値を取る時しか2次方程式の解は存在しませんが、
複素数まで世界を広げると、2次方程式はいつでも解を持つことになります。
ただし、解の種類は判別式$D$によって変わります。
解はいつでも存在するが、
それは実数解だったり、虚数解だったりして、
どっちになるかは判別式$D$で決まるよ!
と解釈することになります。
当時の数学者の反応を見てみましょう。
「いやいや、ルートの中が負とか、そんなもん、
数としては認めねーぞ!!」
これがアンサーでした。
いつの世も新たな数とは受け入れがたいものなのです。
しかし、3次方程式の解の公式を計算していた時に革命が起きます。
$ax^3+bx^2+cx+d=0$の解の公式は、
$x=-\dfrac{b}{3a}+\sqrt[3]{A}+\sqrt[3]{B}, $
$-\dfrac{b}{3a} +\omega \sqrt[3]{A}+\omega^2 \sqrt[3]{B}, $
$-\dfrac{b}{3a} +\omega^2 \sqrt[3]{A}+ \omega \sqrt[3]{B}$
となります。ただし、$\omega =\dfrac{-1+ \sqrt{3}i}{2}$です。
3次方程式の解の公式についてはこちらの記事をご覧ください。

3次方程式の解の公式の何が革命かというと、$\omega$です。
$\omega$は$i$を含んだ数であり、虚数です。
そう。
解の公式に虚数単位$i$が出現してしまったのです!
これで今までとは訳が違ってきます。なにせ公式ですから。
2次方程式では、判別式が負の場合に虚数が登場するにしても、
解の公式の見かけ上には$i$が表立って登場することはありませんでした。
しかし、3次方程式の場合は、公式に堂々と$\omega$が登場します。
$i$なしでは公式の記述すらできないのです。
これはさすがに$i$を数として認めざる負えません。
そうしないと前に進めないからです。
そして、苦し紛れに$i$をこうネーミングします。
Imaginary number
つまりは虚数、というわけです。
虚数単位はこの頭文字をとって$i$と表されることになりました。
虚数単位$i$よ、お前はどこにいるのだ!?
さて、数学者たちはしぶしぶ虚数単位$i$を数として認めることにしました。
$i$が数の仲間入りをしたわけです。
そうなると、今までの数に成り立っていたことが新しい数にも成り立つかな?
という確認作業が始まります。
我々が今まで獲得してきた数には大小関係が定義されていました。
そうなると、次の問題として、$i$がどこにいるかが問題になります。
数と数の位置関係を考えるうえで、
当時の数学者たちが持っている道具は数直線のみです。(あと座標も)
というわけで、
$i$よ、お前は数直線上のどこにいるのだ!?
という疑問が発生します。
至極当然な疑問です。
とりあえず0より大きいのか、小さいのかが知りたいので、順に調べていきます。
① $0<i$と仮定する
$0<i$の両辺に$i$をかける。
このとき、$0<i$であるので、符号の向きは変わらない。
よって$0×i<i^2$となり、
$i^2=-1$であるから
$0<-1$が導かれ矛盾
② $i<0$と仮定する
$i<0$の両辺に$i$をかける。
このとき、$i<0$であるので、符号の向きが変わる。
$i^2>0×i$となり、
$i^2=-1$であるから
$-1>0$が導かれ矛盾
以上のことから分かること。
$i$は数直線上には存在しない!!
当時の数学者からしたら、びっくり仰天でしょう。
数直線が数のすべてだと思っていったのに、それで表せない怪物が登場してしまったのです。
まさに新時代到来!!!
そしてこの問題に終止符を打ったのがガウスという天才でした。
ガウスは天才オブ天才とでも呼ぶべき存在で、(偉大さを表現するのに言葉が足りない)
数学四天王にも選ばれています(僕調べ)。
では、ガウスがどんな発想で虚数単位$i$を捉えていったのか見ていきましょう!
ガウスの発想、その本質は「回転」
虚数単位$i$は数直線上には存在しない、という衝撃的事実が明らかになりました。
でも、$i$を数と認めた以上は、従来の数との位置関係が記述できないと腑に落ちません。
そこでガウスはこう考えます。
行き詰まったら、定義に立ち戻ろう!
$i^2=-1$です。
つまり、ー1が手掛かりとなります!
ガウスはまずー1の性質を思い出すことにしました。
ー1の性質としては、なんといっても
$(-1)×(-1)=1$
です!
ー1の性質の本質は掛け算だ!と見出したガウスは、ひたすらー1をかけてみます。
研究手法の王道、観察です。
(実際にそうしたかは最早確かめようがないですが、そうするとガウスの発想が自然に思えます。)
$(-1)×(-1)=1$
$(-1)×(-1)×(-1)=-1$
$(-1)×(-1)×(-1)×(-1)=1$
$(-1)×(-1)×(-1)×(-1)×(-1)=-1$
さぁ、観察をしたら規則性を見出していきましょう。
ガウスの感想(推測)はこうです。
右辺、1かー1しか出現しなくね!?
なんか1とー1をグルグル回ってね!?
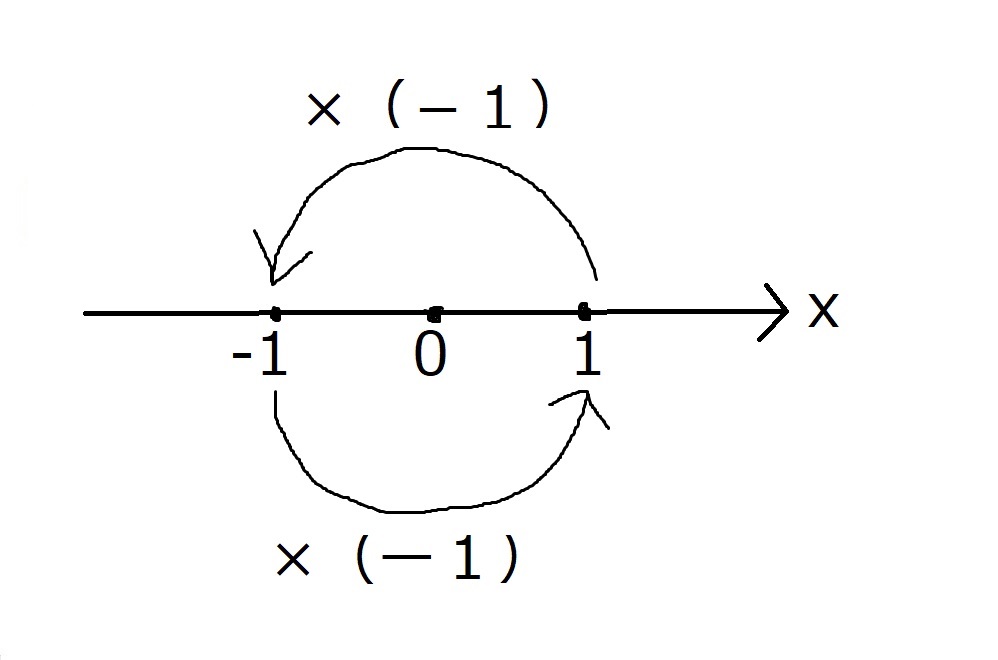
これらの観察から、ガウスはこんなことをひらめきます。
×(ー1)は、180°回転に対応する!!
さて、ここで話を$i$に戻しましょう。
$i^2=-1$です。
そして、(ー1)は180°回転に対応します。
つまり、$i$の定義式は、こう言い換えることが可能です。
$i$を2回かけると、180°回転になるよ!
では$i$を1回かけたら?
90°回転!!
×$i$は90°回転に対応するのです!!!
よって、$i$は数直線の原点の真上に存在することになります。

どうですか?
ガウスが天才オブ天才と呼ばれる所以が垣間見えたと思います。
$i$は数直線の上空にいるのですから、そりゃいくら数直線を見渡しても見つからないわけです。

これで$i$と数直線の位置関係は確定しましたが、$i$と$-i$だけ数直線から飛び出しているのは、なんか釈然としません。
そこで、$i$と$-i$を線で結んでみます。
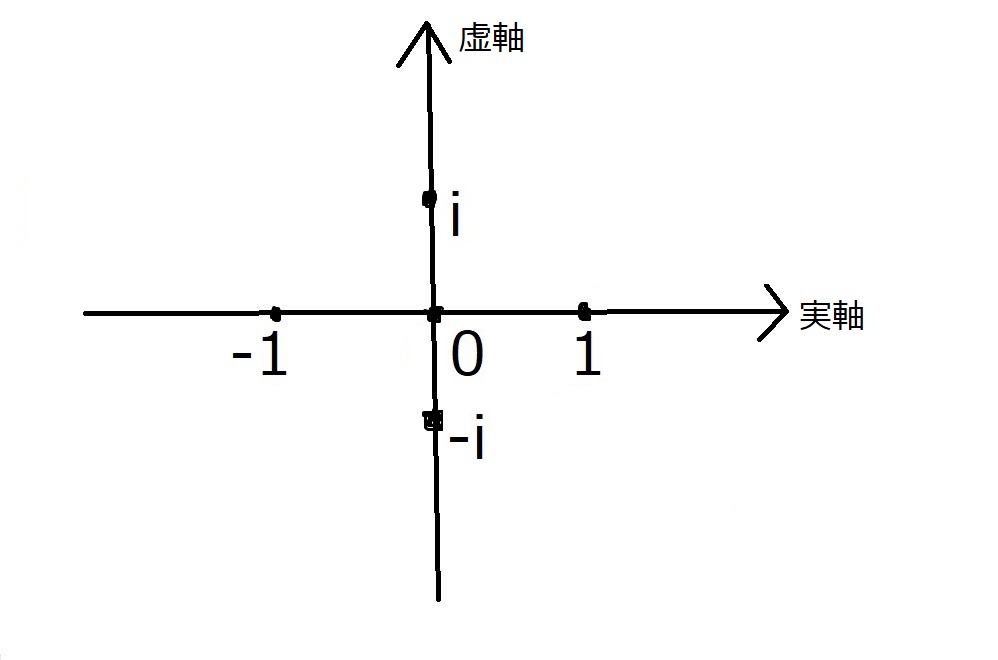
平面が出来上がりました!
複素数は、数直線ではなく、平面で捉えるべき研究対象だったわけです。
ちなみに、横軸を実軸、縦軸を虚軸と言います。
かくして、複素数$a+bi$をあたかも平面上の座標の点かのごとく扱えるようにまりました。
例えば、$1+2i$なら、下の図のような場所にあります。
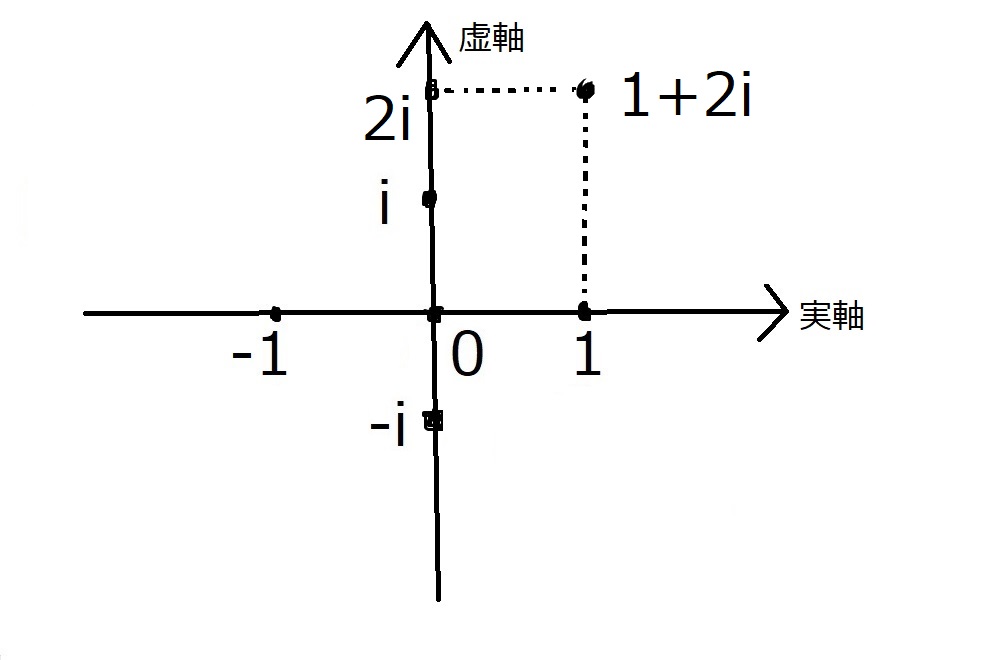
この平面を複素数平面といいます。
もしくは、ガウスに敬意をこめてガウス平面と呼ぶこともあります。
数学を研究するときの視点に興味を持った方は、こちらの記事をどうぞ!
複素数の応用と、その先に見える世界
$i$の応用は、実はめっちゃすごく多方面にわたります(すごすぎて語彙力が低下中)。
ちょっと思いつくだけでもこれだけの応用があります
㋐ 電流の交流回路の計算
㋓ フーリエ変換(携帯の電波とか)
㋒ シュレディンガー方程式(量子力学の波動方程式)
㋓ 四元数(3Dゲームの視点変換、つまりは3次元の回転の記述に使われる)
㋔ 八元数(弦理論への応用あり)
㋐~㋒は、要するに波と$i$は相性がいいよ!というに尽きます。
数学Ⅱで習う通り、波は三角関数で表されるので、
三角関数と$i$は仲良し、ということになります。
これがどのくらい仲良しなのかは、オイラーの公式
を一目見るとすぐ分かりますので、そのうち紹介しようと思います。
また、大学の学部生は学年が進むと複素解析というものを習います。
高校で習う微分・積分を複素数の範囲でやってみよう!という試みなのですが、
多分、学部生が授業で出会う数学の中で最も美しいです。
これもそのうち記事で取り上げていきたいと思います。マジすごです!
㋓、㋔の四元数と八元数は、純粋に数学的な興味から産み落とされました。
複素数は$\mathbb{C}=\lbrace a+bi \mid a, b \in \mathbb{R} \rbrace $です。
ここで、$a+bi$は、二項の式。
これの項数をもっと増やせないかな?というノリです。
複素数をさらに一般化してみよう!というやばいことを思いついた数学者がいたのです。
ハミルトンさんといいます。ハミルトンさんは四元数を発見します。
四元数$\mathbb{H}= \lbrace a+bi +cj +dk \mid a, b, c ,d \in \mathbb{R} \rbrace$
さらにその先の世界、八元数というものを発見する者も現れます。ケーリーさんです。
八元数$\mathbb{O}=\lbrace a+bi_1 +ci_3 +di_4+ei_5+fi_6+gi_7 \mid a, b, c, d, e, f, g \in \mathbb{R} \rbrace$
です。このノリでいくなら、次は16元数が誕生しそうですが、それはおきません。
16元数を考えること自体はできるのですが、16元数は代数として持っていてほしい性質を持ち合わせません。
考えてもあまり嬉しいことがないのです。
代数として持っていてほしい性質、というあいまいな言い方をしましたが、この性質にはちゃんとした名前があり、
ノルム多元環といいます。
「ノルム」というのは長さ的なものを思ってください
「環」とは、分配法則$a(b+c)=ab+ac$が使える世界と思ってください
「多元」は項数と思ってください。実数は1次元、複素数は2次元、四元数は4次元、八元数は8次元です。
ノルム多元環という性質を持つのは実数、複素数、四元数、八元数のみであることが証明できます。
この証明もそのうち記事で取り上げたいと思っています。
そして、純粋に数学的な興味から開発された道具が、
時を超えて3Dゲームや素粒子物理の弦理論に応用されているのですから、驚きと感動があふれてしまいますね。
まとめ
いかがでしたか?
虚数単位$i$を回転という観点から説明しました。
・×(ー1)は180°回転
・×$i$は90°回転
・ゆえに複素数は数直線ではなく平面で捉えるべき研究対象である(複素数平面)
・複素数の応用は沢山!特に波と相性がいい
・更に先の世界があり、四元数、八元数がある。
・八元数が終点
教科書だけでは味わえない虚数単位$i$の物語を楽しんでいただけたなら、とても嬉しいです。
また次回の記事でお会いしましょう!
ガウスさん

See page for author, Public domain, via Wikimedia Commons


コメント