中学で習う三平方の定理。
あれは直角三角形についての定理でした。
これを一般の三角形の場合に拡張できないかな?
というのが今回のお話。
三平方の定理と余弦定理
中学3年生で我々は三平方の定理という偉大な定理と出会います。
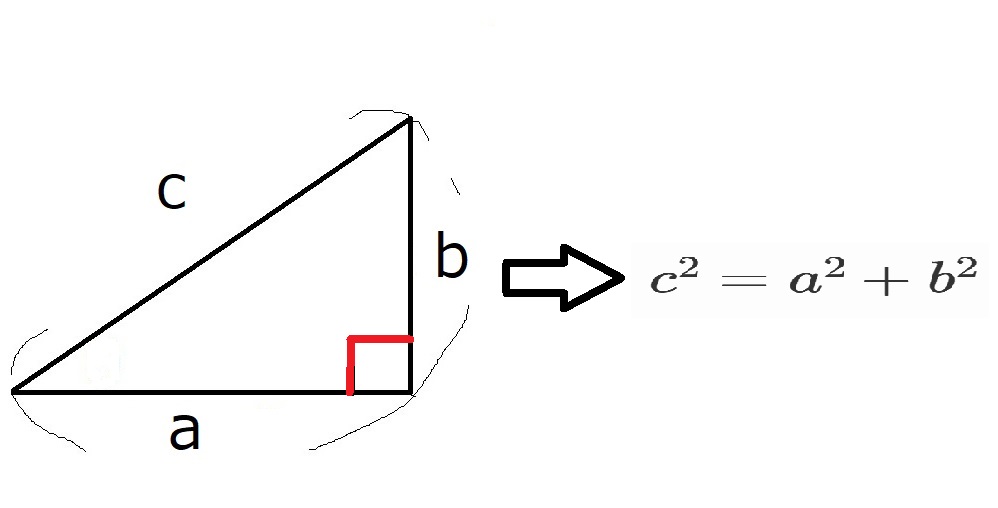
これは直角三角形についての定理でした。
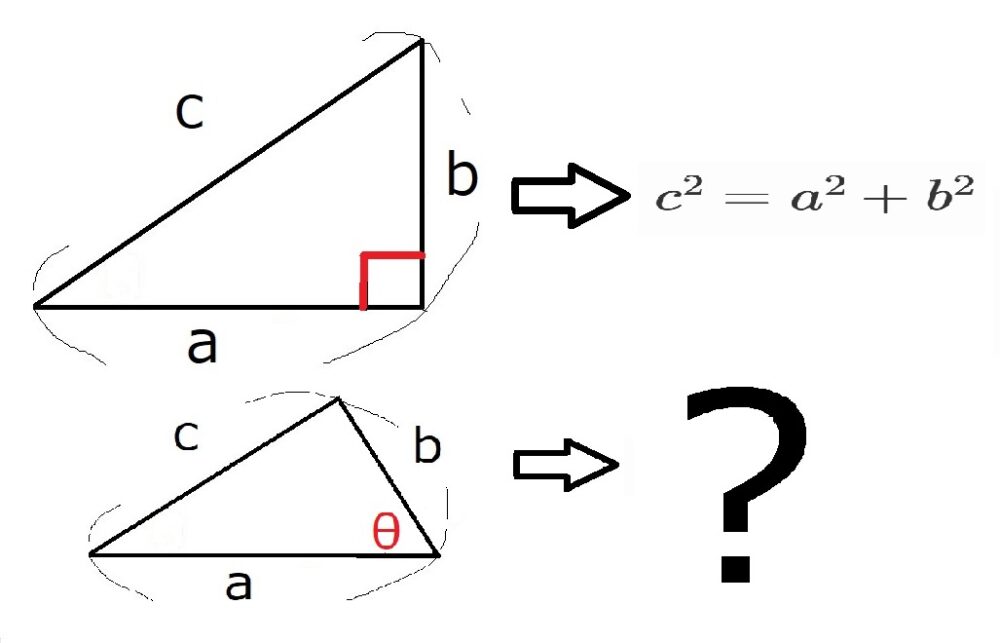
この三角形の直角だった部分を$\theta$に変えてみます。
三平方の定理はどのように一般化されるでしょうか?
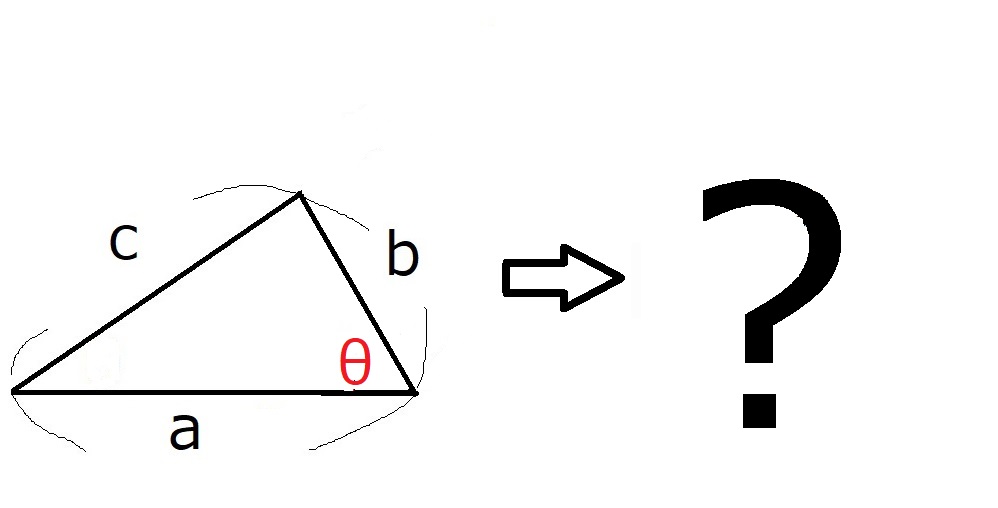
結論から述べると、三平方の定理は余弦定理に進化します。
(定理)
$⊿ABC$について、$AB=c, BC=a, CA=b, ∠ACB=\theta$と置くと、以下が成り立つ
$c^2=a^2+b^2-2ab\cos \theta$
今回はこれを証明していきます!
証明
~脳内会議~
今回も、条件と結果を分けて考えていくことが大切になります。
$⊿ABC$について、$AB=c, BC=a, CA=b, ∠ACB=\theta$と置くと、以下が成り立つ
$c^2=a^2+b^2-2ab\cos \theta$
緑マーカーが条件で、黄色マーカーが結果です。
今回は条件からピックアップすべきキーワードは、特になさそうです。
図だけかいておきましょう。
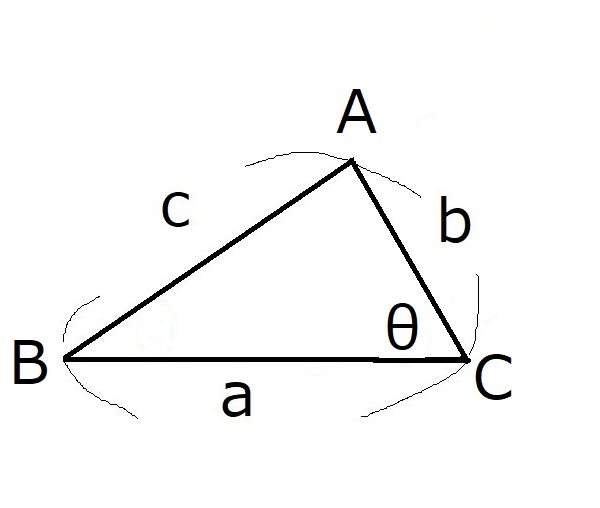
次に、黄色マーカーの結果に着目します。
すると、「コサインが登場している」という点に目が向くと思います。
先ほどの図にコサインを召喚しないといけません。
コサインを召喚する呪文は3つ!
①基準となる長さ
②角度$\theta$
③直角
今回も直角が必要になるので、補助線を引いていくことになります。
コサインを召喚する呪文に違和感がある方は、こちらの記事をご覧ください。

なお、正弦定理の時と同様に、今回も$\theta$が鋭角の場合と鈍角の場合で場合分けが発生します。
ではいってみましょう!
(証明)
$i)$ $\theta$が鋭角の場合
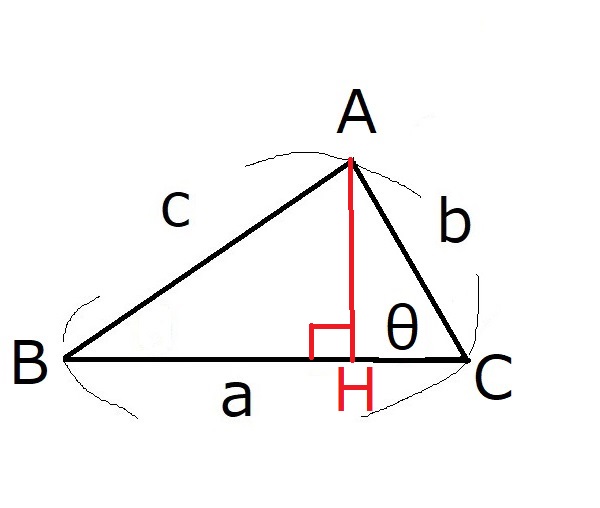
$頂点Aから辺BCに下した垂線の足をHとする。$
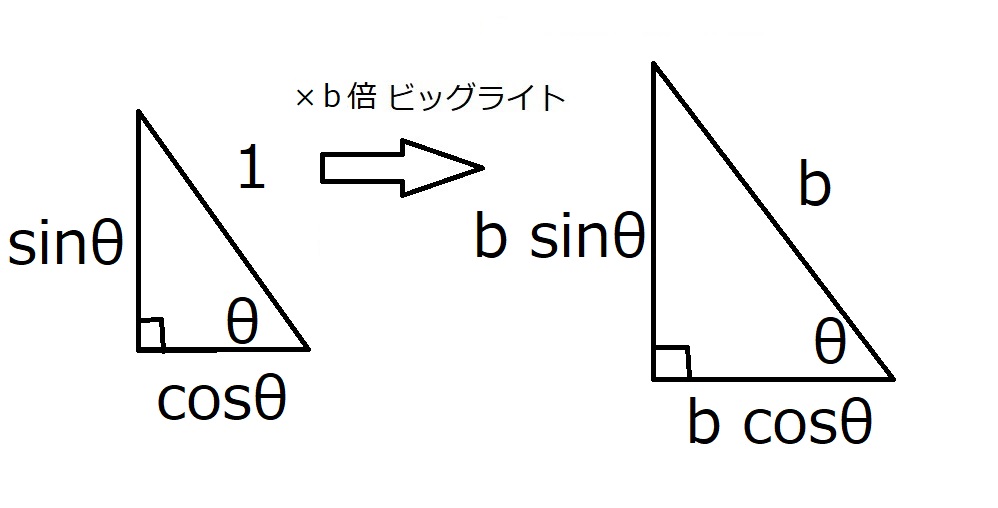
すると三角比の定義より、
$⊿ACH$について、
$AH=b \sin \theta$
$CH=b \cos \theta$
であることが分かる。
ここで、$⊿ABH$について考える。
$BH=BC-CH$
なので、$BC=a, CH=b \cos \theta$を代入すると、
$BH=a-b \cos \theta$
と分かる。
ここで、$⊿ABH$について三平方の定理より、
$c^2=(b\sin \theta)^2 +(a-b \cos \theta)^2$
である。
$c^2=b^2 \sin^2 \theta +(a^2-2ab\cos \theta +b^2\cos^2\theta)$
$c^2=a^2+ b^2\sin^2\theta +b^2\cos^2\theta -2ab\cos \theta$
$c^2=a^2+b^2(\sin^2 \theta +\cos^2 \theta)-2ab\cos \theta$
$\sin^2+\cos^2=1$より、
$c^2=a^2+b^2-2ab\cos \theta$
となる。
$ii)$ $\theta$が鈍角の場合
$\cos (180°-\theta)=-\cos \theta$と
$\sin (180°-\theta)=\sin \theta$
は証明なしで活用できることとする。←そのうちこれ形のまとめ記事出します。
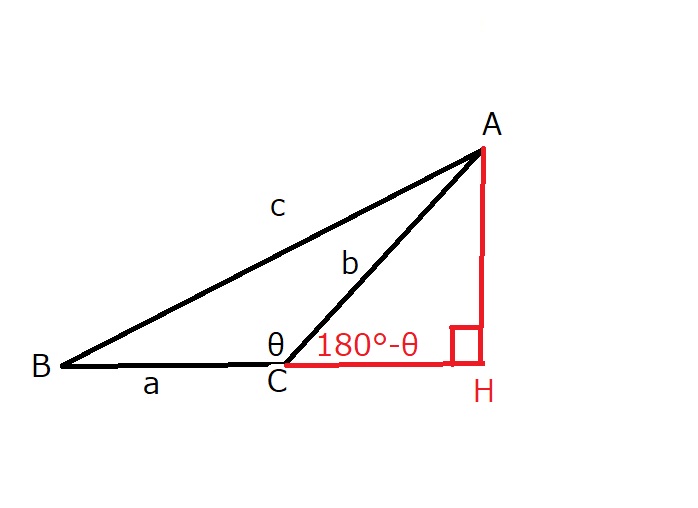
$頂点Aから直線BCに下した垂線の足をHとする。$
$⊿ACH$について、
三角比の定義より、
$AH=b\sin (180°-\theta)$
$CH=b\cos (180°-\theta)$
である。
ここで、$⊿ABH$について、
$BH=BC+CH$
であり、$BC=a, CH=b\cos (180°-\theta)$なので、
$BH=a+b\cos(180°-\theta)$であり、
$\cos (180°-\theta)=-\cos \theta$
であるから、
$BH=a-b\cos \theta$
となる。
また、$AH=b\sin (180°-\theta)$
であり、$\sin (180°-\theta)=\sin \theta$
を使うと、
$AH=b\sin \theta$
ここで、$⊿ABH$について三平方の定理より、
$c^2=(b\sin \theta)^2+(a+b\cos \theta)^2$
となり、右辺を展開して整理すると
$c^2=a^2+b^2-2ab\cos \theta$
となる。
$i), ii)$より、余弦定理が証明された。
(証明終了)
ちなみに、
$c^2=a^2+b^2-2ab\cos \theta$に
$\theta=90°$を代入してみましょう。
$\cos 90°=0$であることを知っていれば、
$c^2=a^2+b^2-2ab\cos 90°$
から
$c^2=a^2+b^2-2ab×0$
$c^2=a^2+b^2$
となって、ちゃんと三平方の定理が出現します。
この意味で、余弦定理は三平方の定理の一般化と捉えることができるのです!
まとめ
いかがでしたか?
余弦定理を三平方の定理の一般化として捉えてみよう!
というのが今回の記事の趣旨です。
三平方の定理って一般化できたんだ!
と楽しんでいただけたら幸いです。
ではまた次の記事でお会いしましょう!
コメント