合同式の世界の逆元の個数を調べたいというきっかけから導入された
オイラー関数。
今回は、オイラー関数にまつわる重要な性質である乗法性の証明をします。
めっちゃ丁寧に解説をした結果、証明がクソ長くなったので、
証明の思考過程や発想法も含めてしっかり理解したいぜ!
という人以外はブラウザバックしてください。
オイラー関数の乗法性
オイラー関数$\phi (n)$とは,
$1, 2, 3, \cdots, n$
のうち、$n$と互いに素なものの個数を表します。
例えば、$\phi(5)$の場合は、
1,2,3,4,5
のうち、5と互いに素なものは
1,2,3,4
の4つなので、
$\phi(5)=4$です。
前回の記事でオイラー関数の値を色々と具体的に調べていった結果、
$m, n$が互いに素な場合は、
$\phi (mn)=\phi(m)\phi(n)$
が成り立つのではないか?
という予想が得られました。
今回はこれを証明して定理に進化させてあげようと思います。
また、オイラー関数の値を観察する過程自体が結構楽しいので、
よろしければ前回の記事ものぞいてみてください。

証明までの発想
まずは示したい内容を確認しておきましょう。
(定理)
$m, n$が互いに素な場合は、
$\phi (mn)=\phi(m)\phi(n)$
~脳内会議~
毎度のことながら、証明というのは何から手を付ければよいのかさっぱりです。
困ったら$\phi(mn)$の定義に立ち戻りましょう。
$\phi(mn)$は、
$1, 2, 3, \cdots, mn$
までの数で、$mn$と互いに素なものの個数です。
今回の定理を示すには、この個数が$\phi (m)\phi(n)$と一致すればよいことになります。
次に問題となってくるのは、$\phi(m)×\phi(n)$をどう処理していくかです。
ひとまず、$\phi(m)$も$\phi(n)$も個数を表していることを留意しておきましょう。
$\phi(m)$も$\phi(n)$は、個数と個数の掛け算を表しています。
要するに、$\phi$という難しい記号を使っていますが、
「一つの袋に3つリンゴが入っています。
4人に袋を配りました。
リンゴは何個ですか?」
と似たような状況ということです。上のリンゴの問題を図にすると、こうなります。
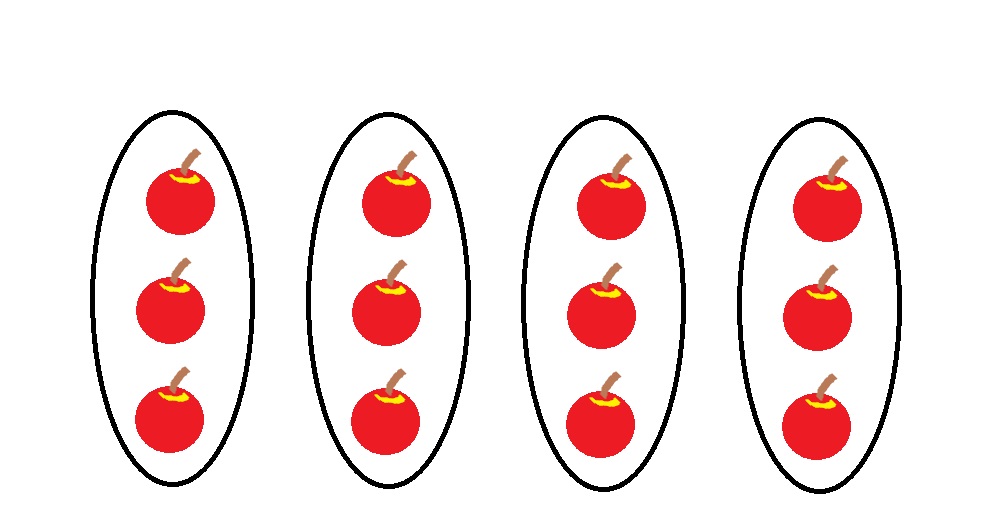
つまり個数の掛け算は、数える作業を長方形で捉えている、と解釈することができます。
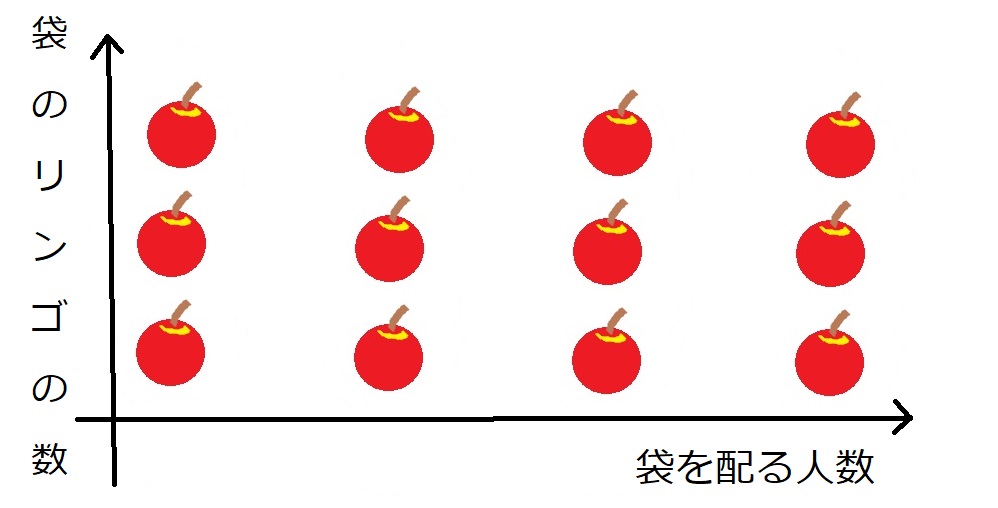
リンゴの問題の場合は、縦軸に袋一つあたりのリンゴの個数、
横軸に袋を配る人数をとっています。
これと同じように、$\phi(m)×\phi(n)$も長方形で捉えて処理していくべきです。
(この作業を大学数学では「直積を取る」と表現したりします)
では、実際に長方形を作っていきますが、いきなり$m$とか$n$とかを使って
文字で計算を進めていくのはあまり実感が沸きません。
また、何を縦軸、何を横軸にするかも文字だとちょっとイメージしにくいので、
まずは具体例で考えていきましょう。
例えば、$m=3, n=5$で考えていきます。
$3と5$は互いに素です。
$\phi(15)=\phi(3)\phi(5)$
が成り立つことを確認します。
まず$\phi(3)$から。
1,2,3のうち、3と互いに素なのは1と2です。
毎回「1,2,3のうち、3と互いに素なのは1と2です」と書くのは大変なので、
「1,2,3のうち、3と互いに素なもの全体」を「$A_3$」と表すことにします。
要するに、
$A_3= \lbrace 1, 2, \rbrace$
です。
$\phi(5)$も同じように考えます。
1,2,3,4,5のうち5と互いに素なものは1,2,3,4なので、
$A_5=\lbrace 1,2,3,4\rbrace$
と置きます。
ここで、縦軸に$A_3$、横軸に$A_5$を取って座標(長方形)を作りましょう。
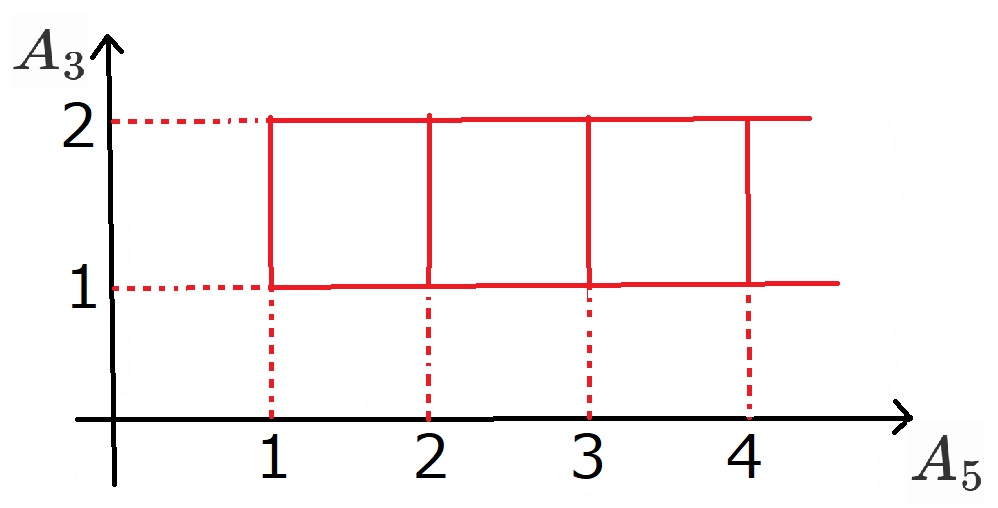
これで$\phi(3)×\phi(5)$の処理は終わりました。
次に$\phi(15)$を考えていきます。
1,2,3,…,15のうち、15と互いに素なものの個数を数えるのですが、
先ほどつくった座標(長方形)を上手く利用します。
例えば、1,2,3,…,15の中から8をチョイスしましょう。
8を3で割った余りは2で、2$ \in A_3$です。
同じように、8を5で割った余りは3で、3$\in A_5$です。
よって、8は先ほどの長方形の$(A_3, A_5)=(3, 2)$のところにプロットされます。
このようにして、先ほど作った座標(長方形)に数をプロットしていきます。
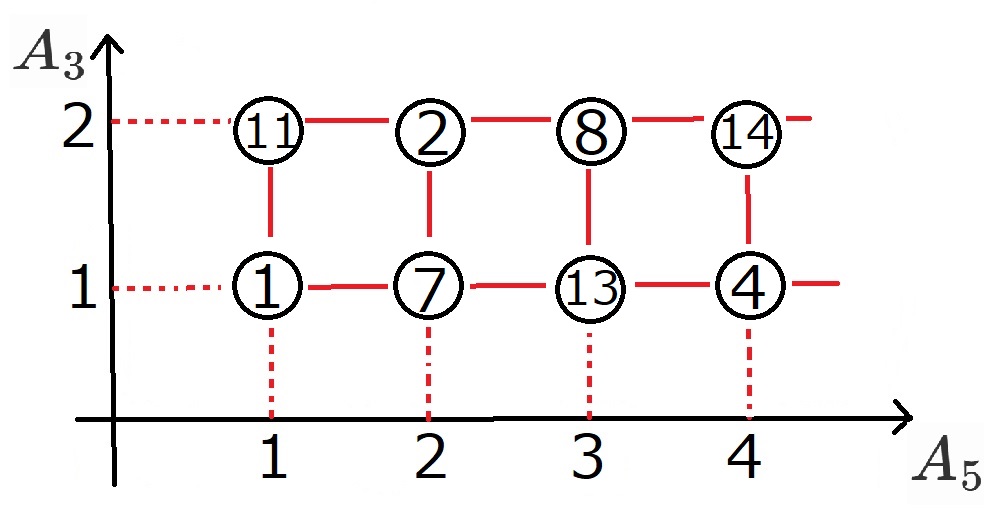
すると、上の図のような感じで
1,2,3,…,15のうち、15と互いに素なやつらが
過不足なく網羅されます!!
過不足なく網羅される、という点が重要なポイントです。
こうして、
長方形に現れる点$(A_3, A_5)$全体の個数と$A_{15}$の個数が一致することが確認できたので、
$\phi(3)×\phi(5)=\phi(15)$
が成り立つ、と結論付けることができるわけです。
あとは、この作業を文字を使って$m, n$で示していけば完了となります。
証明のアウトラインを整理すると、
① 縦軸$A_m$と横軸$A_n$を導入し、$A_{mn}$の元を割り振っていく
② $A_{mn}$の元を適当に1こ取り出して(例の場合は8を取りました)、
それに対応する縦軸の値と横軸の値が存在することを確認する。
(8を3で割った余りは2で、2$\in A_3$とかやっていた確認作業のことです)
③ つくった座標$(A_m, A_n)$に$A_{mn}$の元が
過不足なくプロットされることを確認する
(過不足なく網羅される、という概念を数学では全単射と表現したり、
一対一対応すると表現したりするのですが、これの処理が中々厄介です。
椅子取りゲームを想像すると分かりやすいので、これを例に補足説明します。
椅子が5つあって、5人の人々がそれぞれの席に座っている状態が理想で、
椅子と人が一対一対応している状況です。
同じ椅子に2人の人が座っていたら駄目です(単射と言います)
空席があったりしても駄目です。(全射と言います)
これを$A_m, A_n, A_{mn}$で説明しなおすと、
$A_{mn}$の元が同じ点にプロットされないことと、(単射)
要された座標上の点$(A_m, A_n)$点で、空席になるものがないこと(全射)
の2つを示さないといけません
④ $\phi(m)\phi(n)=\phi(mn)$が導かれる
では頑張っていきましょう!
写像・全射・単射・全単射といった言葉に馴染みのない方は、以下の記事をご覧ください

オイラー関数の乗法性の証明
(定理)
$m ,n$が互いに素なとき、
$\phi(mn)=\phi (m)\phi(n)$
が成り立つ
(証明)
$1, 2, 3, \cdots, m$のうち、$m$と互いに素なもの全体の集合を$A_m$と表す。
同様に、$A_n$と$A_{mn}$を考える。←手順①完了
$A_{mn}$の元$a$を任意にとる。
このとき、$a$を$m$で割った余り$r$が
$A_m$の元となっていることを確認する←手順②開始
$1≦r≦m-1$と
$r$と$m$が互いに素であることを示せればよい。
$r$は$a$を$m$で割った余りなので、
$0≦r≦m-1$である。
ここで、$r \neq 0$であることを背理法で示す。
$r=0$と仮定すると、$a$は$m$の倍数であることになるので、
$a=km$ $(kは整数)$
となる。
したがって、$a$と$mn$は$m$を公約数としてもつことになる。
しかし、$a \in A_{mn}$であり、
$A_{mn}$の元は$1, 2, 3, \cdots, mn$と互いに素でなければならないので、
これは矛盾。
よって、背理法より$r \neq 0$となり、$0≦r≦m-1$と合わせて
$1≦r≦m-1\cdots ㋐$
である。
いま、$a=km+r$
ここで、ユークリッドの互除法より、
$a$と$m$の最大公約数と,
$m$と$r$の最大公約数は等しい。
(式で表すと$GCD(a, m)=GCD(m, r)$)
$a \in A_{mn}$より、$a$と$mn$は互いに素であるので、
$a$と$m$も互いに素である。
したがって、$m$と$r$も互いに素である$\cdots ㋑$
㋐、㋑より、$r \in A_m$であり、
全く同様にして$a$を$n$で割った余りを$r’$とすると、
$r’ \in A_n$も確かめられる。←手順②完了
いま、$c, d \in A_{mn}, c>d$について、
$c$を$m$で割った余りと$d$を$m$で割った余りが等しく、
かつ$c$を$n$で割った余りと$d$を$n$で割った余りも
等しいと仮定する←手順③単射性の確認開始
すると、
$c=q_1m+r_1\cdots ㋒$
$c=q_2m+r_2\cdots ㋓$
$d=q_3m+r_1 \cdots ㋔$
$d=q_4n+r_2 \cdots ㋕$
と表すことができる。 (q_1, q_2, q_3, q_4, r_1, r_2 は整数)
$㋒-㋔$より、
$c-d=m(q_1-q_3)$
となり、$c-d$は$m$の倍数である。
$㋓-㋕$より、
$c-d=n(q_2-q_4)$
となり、$c-d$は$n$の倍数でもある。
$m, n$は互いに素であるので、
$c-d$は$mn$の倍数であることになる。
仮定より$c>d$であるので、
$c-d=mns$ $(s=1, 2, 3 \cdots )$
と表される。
しかし、$c, d \in A_{mn}$であるので、
$1≦c≦mn, 1≦d≦mn$であり、
このことと$c>d$より、
$1<c-d<mn$でなけらばなない。
これは$c-d=mns$ $(s=1, 2, 3 \cdots )$に矛盾する。
ゆえに、$c=d$でなければならず、
$A_{mn}$に属する異なる2つの元が同じ点$(A_m, A_n)$
にプロットされることはない。←手順③単射性の確認完了
ここで、$e \in A_m, f \in A_n$をとる。
このとき$A_{mn}$の元で、
$m$で割った余りが$e$であり、
かつ$n$で割った余りが$f$であるものが
必ず存在することを示す←手順③全射性の確認開始
$m, n$が互いに素なので、中国剰余定理より、
$g \equiv e (\mod m)$かつ
$g \equiv f (\mod n)$となる
$g$ $(0≦g≦mn-1)$がただ一つ存在することが示される。
$g \in A_{mn}$であればよいので、
$1≦g≦mn-1$と
$g$と$mn$が互いに素であることが示されればよい。
$g=0$と仮定する。
$g\equiv e (\mod m)$から、
$e-g$ は$m$の倍数となり、$g=0$なので
$e$は$m$の倍数となる。
しかし、$e \in A_m$であり、$e$は$m$と互いに素でなければならないので
これは矛盾。
よって、$g \neq 0$となり、$0≦g≦mn-1$
と合わせて$1≦g≦mn-1$となる。
以上のことより、
$\phi(m)\phi(n)=\phi(mn)$←手順④終了
よって、
$\phi(mn)=\phi (m)\phi(n)$
である。
(証明終了)
まとめ
ここまで読んでいただきありがとうございます!
今回はオイラー関数の乗法性
$\phi(m)\phi(n)=\phi(mn)$
を示しました。
結構大変だったと思いますが、
この式は理解するだけの価値のあるすごい性質です。
次回はオイラー関数$\phi (n)$を求めるズバッとした公式をゲットしようと思います。
ご期待ください。

コメント