ド・モアブルの定理がいかに美しい定理なのか。
その端的な一例を紹介しようと思います。
ド・モアブルの定理とは?
すべての整数$n$について、
$(\cos \theta +i\sin \theta)^n=\cos n\theta +i\sin n\theta$
が成立する。
というのがド・モアブルの定理です。
もうすでに美しいですね。
今回はこれを応用していきます。
ド・モアブルの定理や極形式という言葉について馴染みのない方は
以下の記事をご覧ください。

1のn乗根を求めてみる
方程式史上おそらく最もシンプルなもの。
それが
$z^n=1$
だと思います。
簡略のため、$n$は整数ではなく自然数としておきましょう。
文字は$x$ではなくて$z$を使っていますが、あまり気にしないでください。
複素数が絡むときは$z$を使うことがなんとなく多いので、それに習いました。
$z^n=1$
を解くにあたって極形式を活用します。
$a+bi=\sqrt{a^2+b^2}(\cos \theta +i\sin \theta)$
というやつですね。
なぜ$a+bi$の表し方ではなくて極形式を用いるのか。
疑問に思う方もいるかもしれないので、
2つの表し方の使い分けの基準を少し補足しようと思います。
基本的に、複素数の掛け算は回転に対応します。
詳しくはこちらの記事をご覧ください。
$×i$を例に回転を説明しています。

回転を扱うにあたっては、角度が出現する極形式の方が圧倒的に扱いやすいのです。
$z^n$は$z$を$n$回も掛け算しているので、極形式を使います。
$z^n=1$の解を
$z=r(\cos \theta +i\sin \theta)$と置きます。←$\sqrt{a^2+b^2}$は式が長くなるので$r$と置きました。
補足ですが、極形式を考えるときは
$0≦\theta<2\pi$と思ってください。
$z=r(\cos \theta +i\sin \theta)$を
$z^n=1$に代入すると、
$\lbrace r(\cos \theta +i \sin \theta) \rbrace ^n=1$
となります。
左辺について、ド・モアブルの定理より、
$r^n(\cos n\theta +i\sin n\theta)=1$
となります。
ここで、左辺が極形式なのに右辺が極形式になっていないのはバランスが悪いので、
1を極形式で表します。
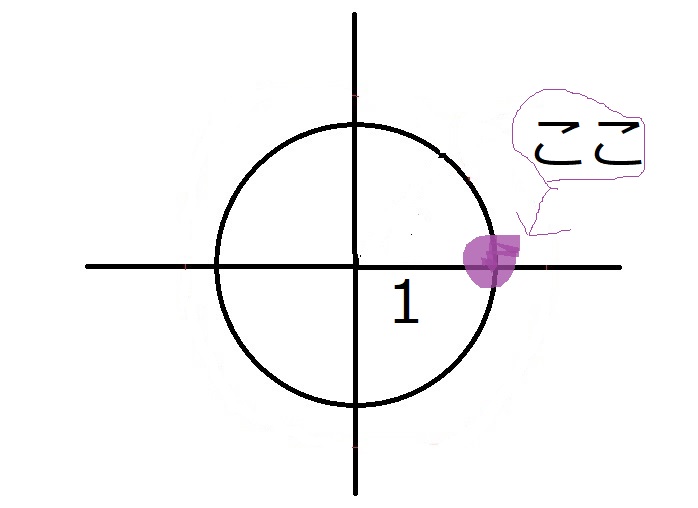
1は複素数平面上の0°の位置にあるので(別に0°じゃなくても$2\pi$とか$4\pi$とかでもいいですが)
$1=\cos 0+i\sin 0$です。
よって、
$r^n(\cos n\theta +i\sin n\theta)=1×(\cos 0 +i\sin 0)$
ここで、極形式の大きさと角度を比べていくことになります。
まずは大きさから比べましょう。
$r^n(\cos n\theta +i\sin n\theta)=1×(\cos 0 +i\sin 0)$
$r^n=1$です。
よって$r=1$ですね。
おいおい、
$r^n=1$で$r=1$なら
$z^n=1$も$z=1$
で終わりじゃねぇの?今までの議論なんだったの?
と思う方もいると思うので(初見の時の僕のことです)補足します。
$r$は、実際には大きさ$\sqrt{a^2+b^2}$を表しています。
大きさが複素数になることはありえません。
大きさは絶対に正の実数です。
それゆえに、$r^n=1$のときは$r=1$としてよいのです。
一方、$z^n=1$の$z$は複素数なので、$z=1$以外にも解が発生します。
だから複素数の極形式で議論を進めていく必要があるのです。
ともあれ、大きさについての議論は終わりました。
$r=1$です。
次は角度を調べていきます。
$r^n(\cos n\theta +i\sin n\theta)=1×(\cos 0 +i\sin 0)$
の左辺について、$0≦\theta<2\pi$ですが、
今回は$\theta$の範囲ではなく$n\theta$の範囲が欲しいので、
$0≦\theta<2\pi$の全体を$n$倍して
$0≦n\theta<2n\pi$です
この範囲で、右辺の角度0と同じ位置にいる奴らを探すことになります。
で、求めたのがこちらです。
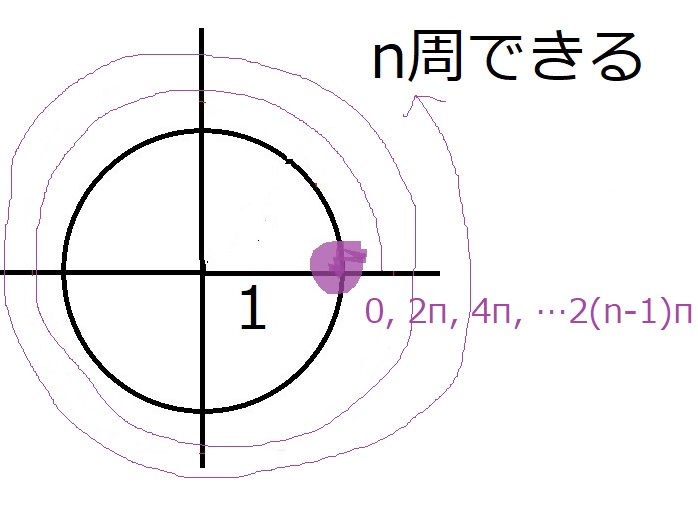
$n\theta=0, 2\pi, 4\pi, 6\pi, \cdots, 2(n-1)\pi$
よって
$\theta=0, \dfrac{2\pi}{n}, \dfrac{4\pi}{n}, \dfrac{6\pi}{n}, \cdots, \dfrac{2(n-1)\pi}{n}$
となります。
いま、$z^n=1$の解を$z=r(\cos \theta+i\sin \theta)$と置いており、
$r=1, \theta=0, \dfrac{2\pi}{n}, \dfrac{4\pi}{n}, \dfrac{6\pi}{n}, \cdots, \dfrac{2(n-1)\pi}{n}$
なので、
$z=\cos \dfrac{2k\pi}{n}+i\sin \dfrac{2k\pi}{n}$ $(k=0, 1, 2, \cdots, n-1)$
となります!!
ヤバくないですか?
何がどうヤバいのか、具体例で説明していこうと思います。
$z^n=1$の解と複素数平面と正多角形と
$n=5$の場合が素朴にビックリすると思うので、この場合を考えてみましょう。
(ペイントの図形にちょうどいい感じに正五角形が搭載されているという都合もあります)
$z^5=1$の解は、先ほどの議論より、
$z=\cos \dfrac{2k\pi}{5}+i\sin \dfrac{2k\pi}{5}$ $k=0, 1, 2, 3, 4$
です。
$\alpha_0=\cos \dfrac{0\pi}{5}+i\sin \dfrac{0\pi}{5}=1$
$\alpha_1=\cos \dfrac{2\pi}{5}+i\sin \dfrac{2\pi}{5}$
$\alpha_2=\cos \dfrac{4\pi}{5}+i\sin \dfrac{4\pi}{5}$
$\alpha_3=\cos \dfrac{6\pi}{5}+i\sin \dfrac{6\pi}{5}$
$\alpha_4=\cos \dfrac{8\pi}{5}+i\sin \dfrac{8\pi}{5}$
と置きましょう。
$\alpha_0 ~\alpha_5$の角度に注目してください。
$\dfrac{2\pi}{5}$刻みになっていませんか?
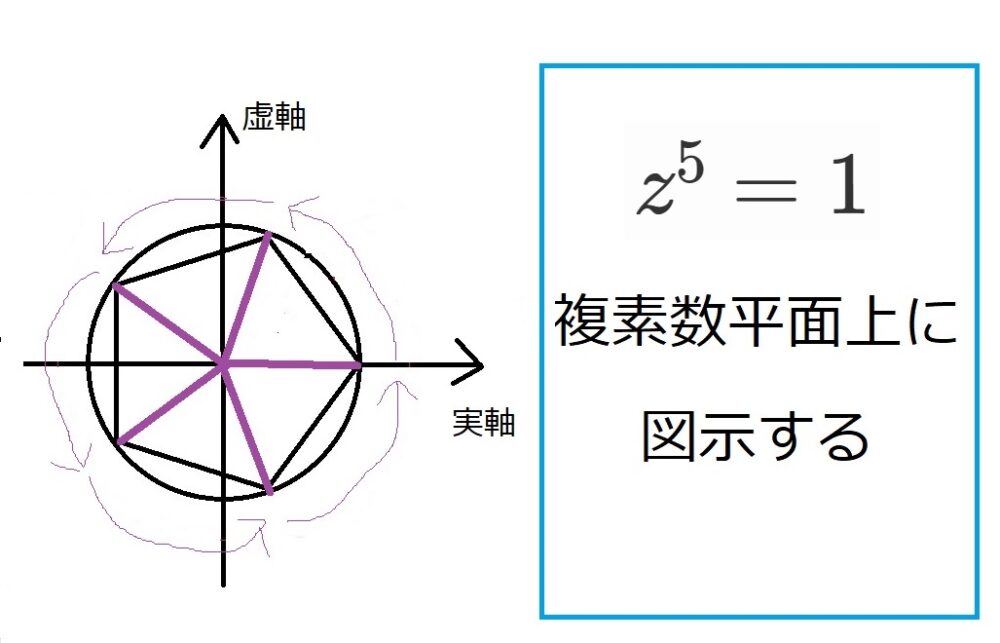
これを複素数平面上に図示すると以下のようになります。
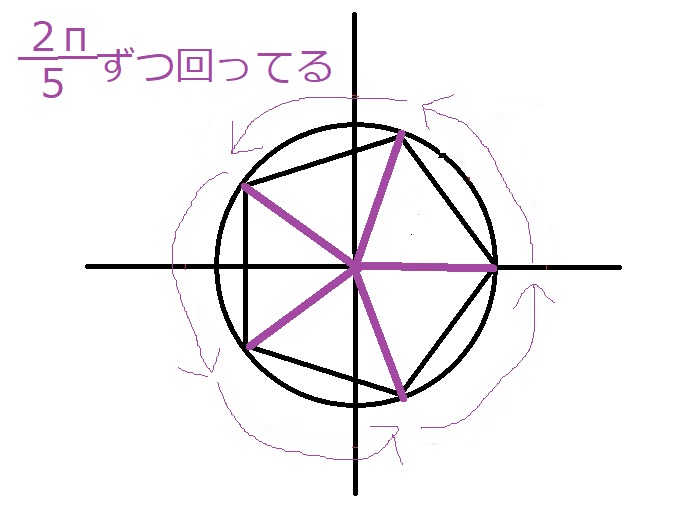
正五角形ができました!!
ヤバいですよね!!!!!
あと、もう一つヤバいことがあります。
先ほどの$\alpha_1~\alpha_5$にド・モアブルの定理を逆向きに使うと、
$\alpha_1=\cos \dfrac{2\pi}{5}+i\sin \dfrac{2\pi}{5}$
$\alpha_2=\cos \dfrac{4\pi}{5}+i\sin \dfrac{4\pi}{5}=(\cos \dfrac{2\pi}{5}+i\sin \dfrac{2\pi}{5})^2=(\alpha_1)^2$
$\alpha_3=\cos \dfrac{6\pi}{5}+i\sin \dfrac{6\pi}{5}=(\cos \dfrac{2\pi}{5}+i\sin \dfrac{2\pi}{5})^3=(\alpha_1)^3$
$\alpha_4=\cos \dfrac{8\pi}{5}+i\sin \dfrac{8\pi}{5}=(\cos \dfrac{2\pi}{5}+i\sin \dfrac{2\pi}{5})^4=(\alpha_1)^4$
一般に、$z^n=1$の解を表す文字としては$\zeta$が採用されることが多いので、
これに習うと、次のようなことが成り立ちます。
$z^n=1$の解は$z=\zeta, \zeta^2, \zeta^3, \cdots, \zeta^{n-1}, \zeta^n(=1)$
であり、これらを複素数平面上に図示すると正$n$角形ができる
まとめ
・ ド・モアブルの定理ヤバい
以上
また次回の記事でお会いしましょう!
コメント