ユークリッドの互除法を面積で考える

ユークリッドの互除法って何に使うの？

ユークリッドの互除法とは、２つの数の最大公約数を求めるための計算方法です。

例えば、６と８の最大公約数を考えてみましょう。

$6=2×3$

$8=2×2×2$

なので、最小公倍数は６と８の最大公約数は２です。

６と８は見た瞬間すぐに素因数分解できるので、簡単に最大公約数を求めることができます。

では、７９１と１２４３の最大公約数はどうでしょう？

すぐには分かりません。

大きい数の素因数分解は、意外と難しいのです。

そこで、ユークリッドの互除法が登場します。

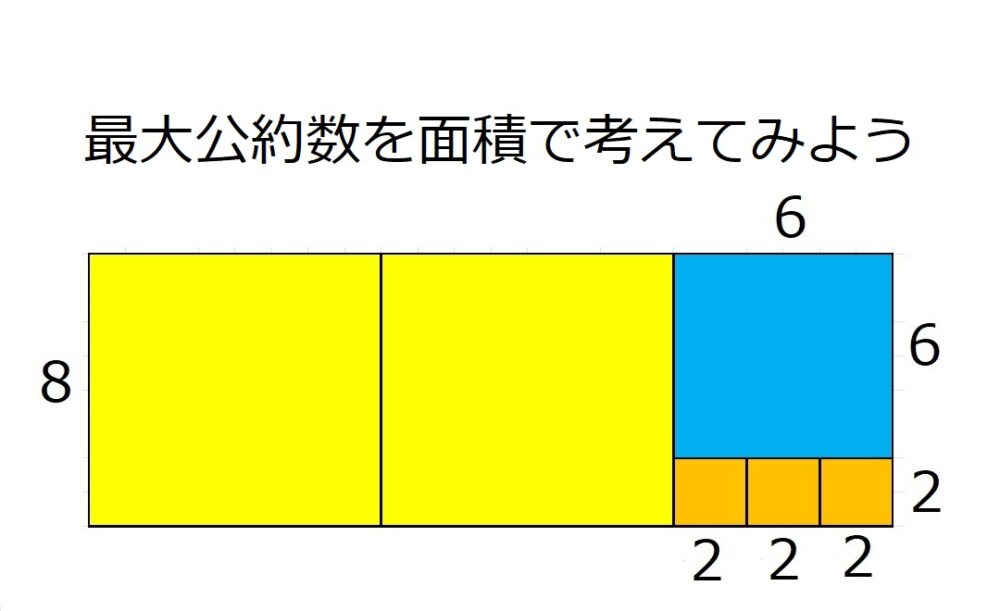
最大公約数を面積で考える発想

ユークリッドの互除法の基本的な発想は、最大公約数を面積で考える、というものです。

簡略のため、ここでは８と２２の最大公約数を考えましょう。

縦の長さが８、横の長さが２２の長方形を考えます。

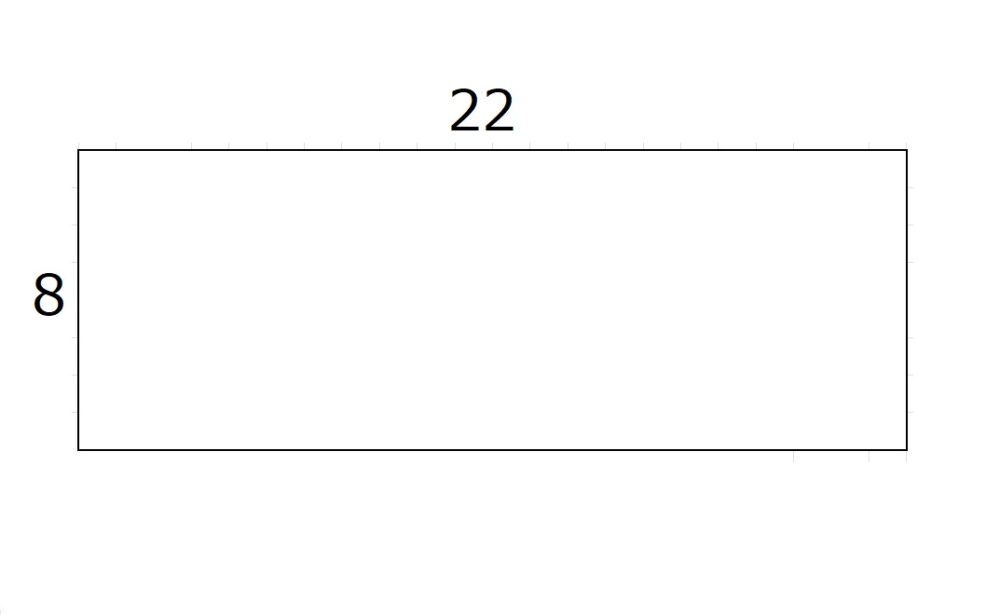
この長方形を、同じ大きさの正方形で敷き詰めていくことを考えます。

例えば、一辺の長さが１の正方形なら、絶対に敷き詰めることがでますよね。

縦に８個、横に２２個正方形を並べて行けば完了です。

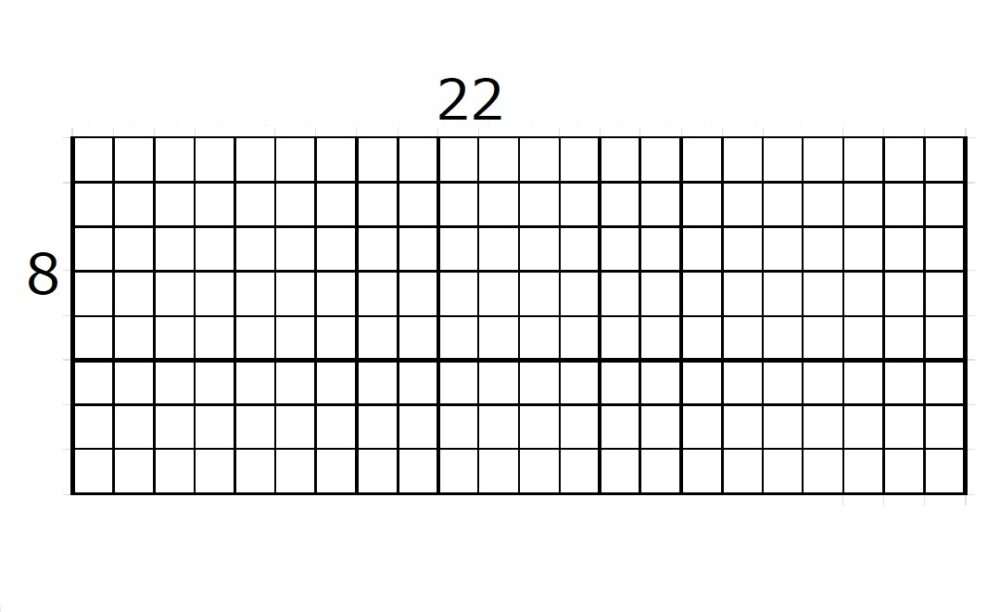
実際に敷き詰めると上の図のようになります。

つまり、１辺の長さが１の正方形であれば、どんな長方形でも敷き詰めができます。

でもこれは当たり前すぎて面白くありません。

最大公約数を考えたいので、１辺の長さが１ではなく、なるべく大きい正方形で敷き詰めをしたいものです。

例えば、一辺の長さが５の場合はどうでしょうか？

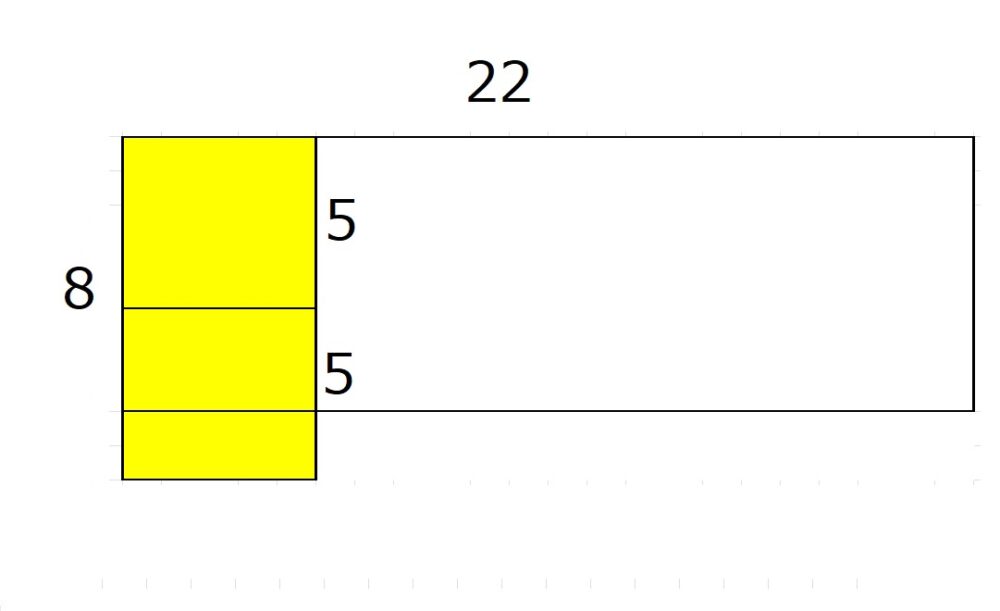
はみ出してしまいました。

一辺の長さが５の正方形では、この長方形は敷き詰めできないようです。

そこでユークリッドさんんはこう考えます。

とりあえず最大限でかい正方形を並べていって、段々小さくすりゃよくね？と。

今回は縦の長さが８、横の長さが２２なので、ひとまず一辺の長さが８の正方形を何個並べることができるか考えます。

２２は８より大きいので、１つは必ず入ります。

では２つ目は？入ります。

３つ目は？８×３＝２４で、２２を超えてしまうので、無理です。

２個まで入りますね。並べてみると、こうなります。

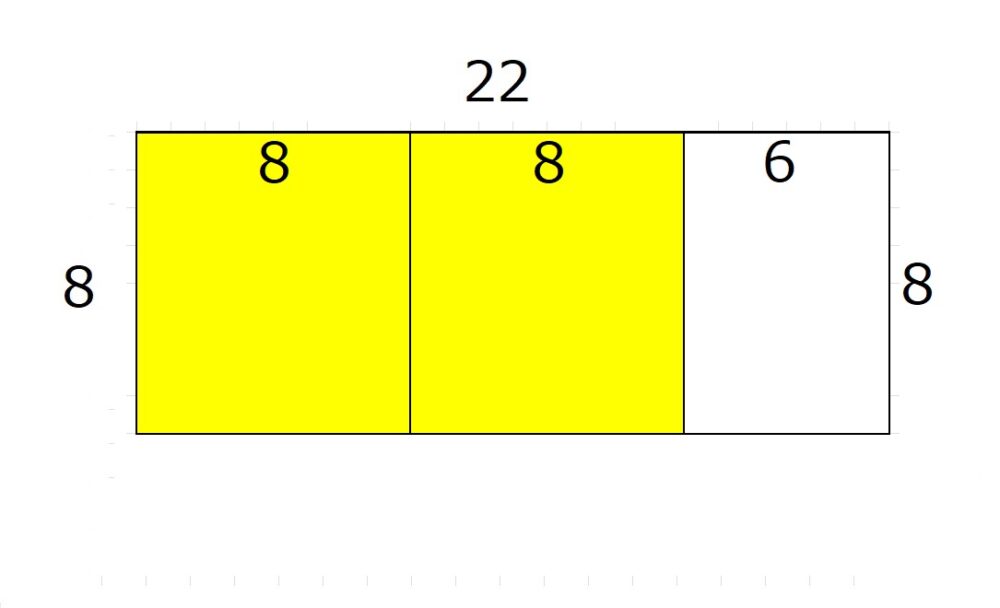
一辺の長さが８の正方形が２個入って、長さが６余ります。

長方形のよこの長さに着目してこれを式にすると、

２２＝８×２＋６　となります。

色のついていない白い長方形に着目しましょう。

縦の長さが８で、横の長さが６です。

今度は一辺の長さが６の正方形を白い部分に入れてみます。

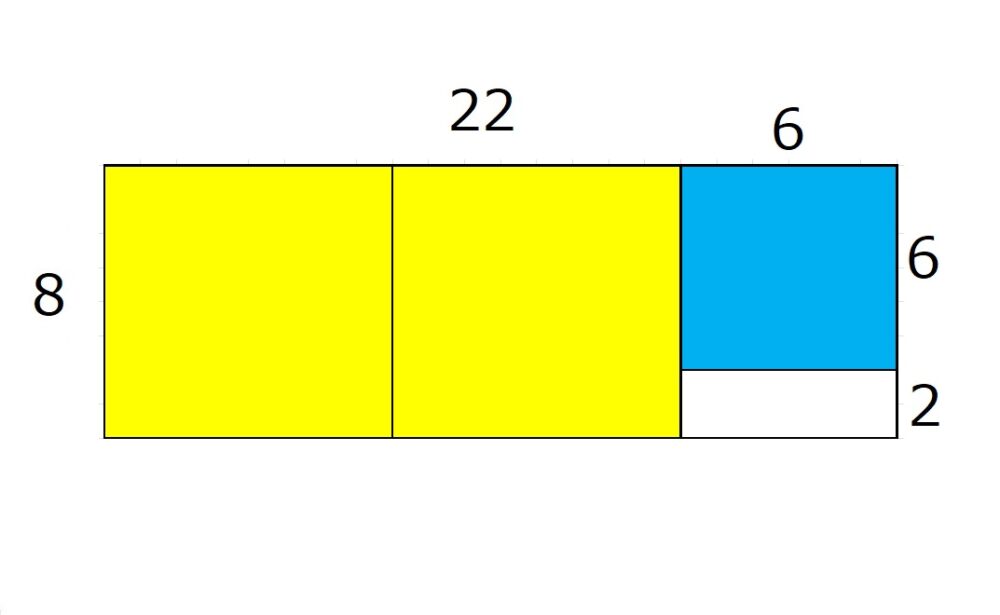
一辺の長さが６の正方形は、１個入って、長さが２余ります。

これを縦の長さに注目して式にすると、

８＝６×１＋２　となります。

さて、まだ色のついていない白い長方形に着目してみましょう。

縦の長さが２、横の長さが６の長方形です。

これに、一辺の長さが２の正方形を入れていきます。

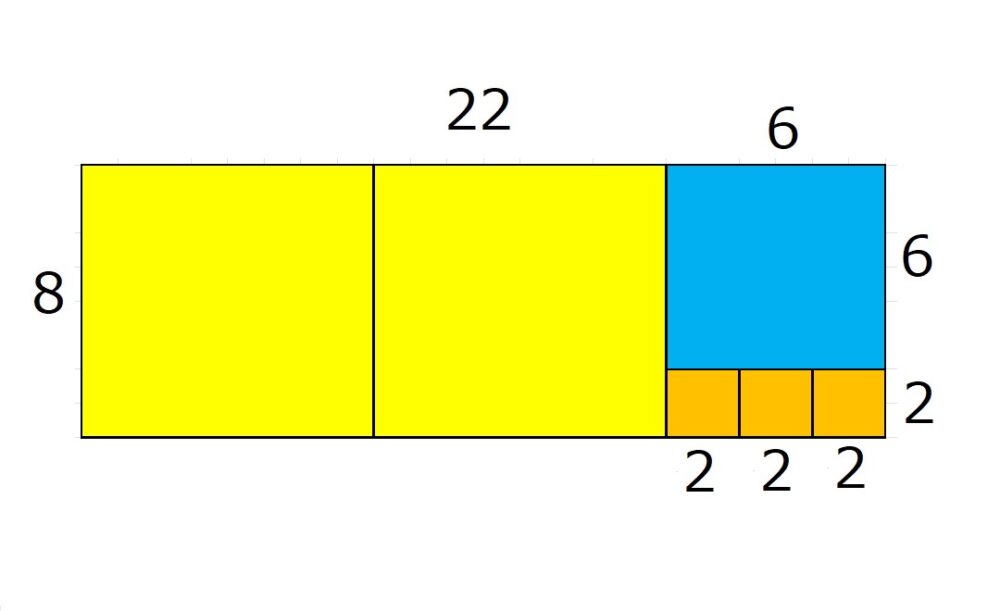
余りなく、ぴったりはまりました！！

これを式で表すと、

６＝２×３＋０　となります。

ぴったりはまったので、今回の最大公約数は２ということが分かりました。

式をまとめると、こうです。

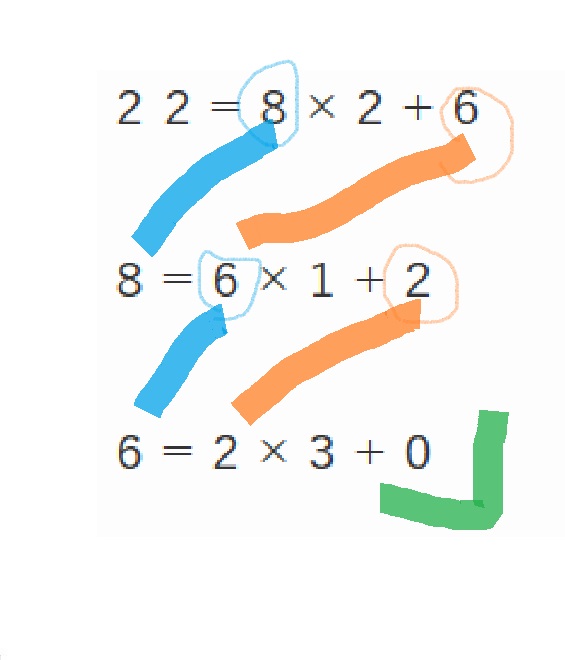
余りが０になるまで繰り返していくところがポイントです。

ちなみに、最大公約数が１の場合はあまりが１になった時点で終わってもかまいません。

このように、割り算を繰り返して最大公約数を求めていく計算を、ユークリッドの互除法といいます。

８と２２くらいなら、わざわざユークリッドの互除法を使うまでもありませんが、

数が大きくなってくるとこれが有効です。

試しに７９１と１２４３の最大公約数を調べてみましょう。

１２４３＝７９１×１＋４５２

７９１＝４５２×１＋３３９

４５２＝３３９×１＋１１３

３３９＝１１３×３＋０

よって、７９１と１２４３の最大公約数は１１３です。

まとめ

いかがでしたか？

ユークリッドの互除法は、意味がよく分からないまま計算手順だけ覚えさせられるものの筆頭ですが、

最大公約数を面積で捉えているという発想を知っていると、多少は風通しがよくなります。

皆さんの学びの一助となれば幸いです。