2次方程式は普通は平方完成を使って解きます。
しかし、別にそれ以外の方法・発想でも解けます。
何に着目するか、問題をどう眺めるか。
ちょっとした違いで千差万別な別解が存在しうるのが数学の楽しいところです。
そして、数学史を切り開いてきたのはいつだってそんな別解たちでした。
今回は2次方程式を対称式を使って解きます。
この考え方が後々ガロア理論につながっていくので、ぜひ楽しんでください。
方程式を対称式で解く発想はどこから来るの?
今回の記事では2次方程式を対称式の考え方で解いていきますが、
まず皆さんにクエスチョンマークが浮かんでいることと思います。
そんな発想、どうやって思いつくんだよ!!
そりゃそうです。
試験対策の勉強をしているだけでは、中々この2つの結びつきは見えてきません。
この記事が方程式に対称式を用いる発想が自然に見える一助となれば幸いです。
キーワードは、「解と係数の関係」と「対称式の基本定理」。
順に考えていきましょう!
両者に馴染みがない方は、以下の記事をご覧ください。


順にみていきましょう。
まず、2次方程式$ax^2+bx+c=0$を解く、
とはどういうことでしょうか?
それは、解を「係数の四則演算と根号によって表現する」ということです。
そして、方程式の解と係数は基本対称式でつながっていました。
解を$\alpha, \beta$とすると、
$\alpha +\beta=\dfrac{b}{a}, \alpha \beta =\dfrac{c}{a}$
となり、これが解と係数の関係です。
一方、基本対称式については、「対称式の基本定理」が成り立ち、
対称式は必ず基本対称式で表すことができます。
つまり、
「二次方程式を解く」→「解を係数で表したい」
「方程式の解」→「解と係数の関係」→「解の基本対称式が係数で表されている」
「対称式の基本定理」→「対称式は必ず基本対称式(つまり方程式の係数)で表される」
このようにして、二次方程式を解く、ということは基本対称式と密接なつながりがあるのです。
文章ばかり見せられても実感が沸かないと思うので、サクサク次に行ってみましょう!
対称式を使って実際に解いてみた
(解答)
$ax^2+bx+c=0$を解く。
解を$\alpha, \beta$とすると、解と係数の関係より、
$\alpha +\beta=\dfrac{b}{a}$
$\alpha \beta=\dfrac{c}{a}$
ここで、$\alpha +\beta =-\dfrac{b}{a}$
なので、もしも$\alpha -\beta$を係数$a, b, c$で表すことができれば、
これらの連立方程式を解くことによって$\alpha, \beta$を係数で表すことができる。
よって、$\alpha-\beta$を係数を使って表していきたい。
しかし、$\alpha -\beta$は対称式ではない。←これ結構ポイントです
そこで、$(\alpha -\beta)^2$を考える←二乗によって対称性を高めています
$(\alpha -\beta)^2$は対称式であるので、基本対称式で表すことができる。
$(\alpha -\beta)^2=(\alpha +\beta)^2-4\alpha \beta$
ここで、解と係数の関係より$\alpha +\beta =-\dfrac{b}{a}, \alpha \beta =\dfrac{c}{a}$
であったので、これを代入すると、
$(\alpha -\beta )^2=(\dfrac{b^2}{a^2})-4\dfrac{c}{a}$
$(\alpha +\beta)^2=\dfrac{b^2-4ac}{a^2}$
よって、
$\alpha -\beta =\pm \dfrac{\sqrt{b^2-4ac}}{a}$
となり、
$\alpha +\beta =-\dfrac{b}{a}\cdots ①$
$\alpha -\beta=\pm \dfrac{\sqrt{b^2-4ac}}{a}\cdots ②$
を連立方程式ととらえて解くと、
$\alpha, \beta =\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
となる。
(解答終了)
体(たい)の考え方から今の過程を眺める
ここで、今までとはまた違った角度で2次方程式の解を眺めてみます。
どんな角度から見るかというと、体(たい)に着目します。
体(たい)という考え方や、既約・可約という表現に馴染みのない方は以下の記事をご覧ください。


方程式を解くことと、体(たい)の考え方は密接に結びついていました。
例えば、$x^2-3=0$は、有理数係数の範囲では既約です。
つまり、解けません。
しかし、係数の範囲を$\mathbb{Q}(\sqrt{3})$まで広げると可約になり、
$x^2-3=(x+\sqrt{3})(x-\sqrt{3})$
と因数分解できます。
つまり解けます。
このように、方程式を解くとは、
係数の範囲を広げる作業
として捉えることもできます。
今回の2次方程式$ax^2+bx+c=0$の場合を考えると、(これは有理数係数で既約なものとします)
係数の範囲を$\mathbb{Q}$から$\mathbb{Q}(\sqrt{b^2-4ac})$まで広げたら解けた!
と捉えることができます。
このように、係数となる体を広げていく過程を体の拡大という言葉で表現します。
今はまだ「ふーん」でOKです。
対称式の発想と、体の拡大の発想を別物として捉えず、
切っても切れない縁で結ばれたものとして眺めた史上最初の数学者の名。
それがエヴァリスト・ガロアであり、
彼の手法をガロア理論といいます。
まとめ
いかがでしたか?
・方程式は対称式を使っても解くことができる。
・方程式を解くことを、係数の体を拡大する作業と捉えることもできる
・両者の考え方を別個のもとして捉えるのではなく、セットで研究したのがガロア
・ガロアはすごい
方程式を解くということ一つとっても、
眺め方が複数あるということを楽しんでいただけたなら最高です。
ではまた次の記事でお会いしましょう!
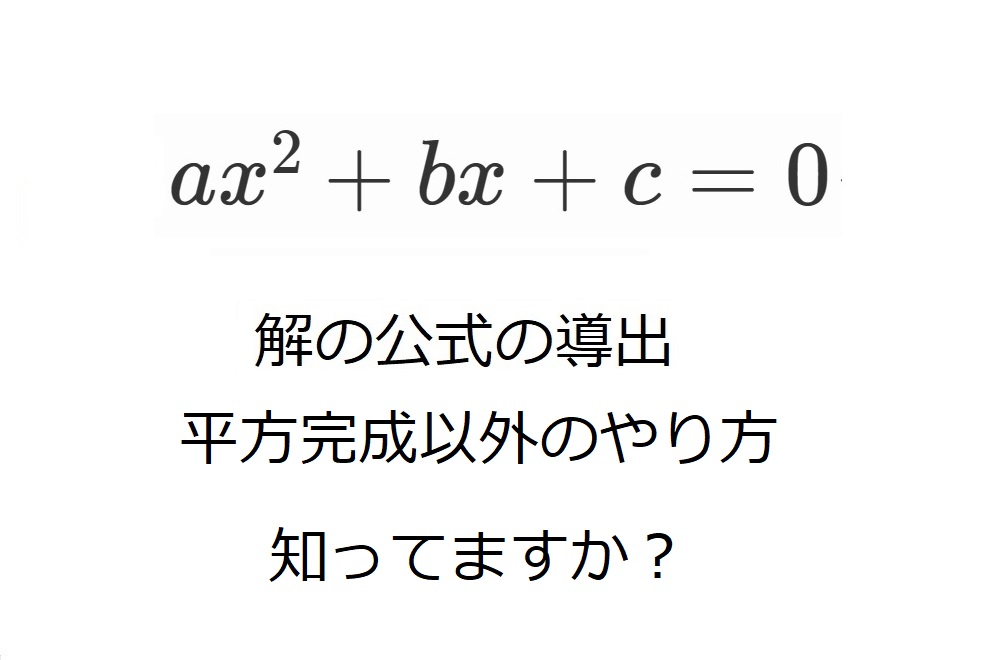
コメント