今回は、4次方程式が解ける仕組みを対称性という視点から理解していきます。
その際、ラグランジュの分解式(ラグランジュ・リゾルベントともいう)が活躍します。
方程式の対称性を調べるとき、ラグランジュの分解式はとても強力な武器なのです。
二次方程式と三次方程式のおさらい
二次方程式$ax^2+bx+c=0$の2つの解を
$x=\alpha, \beta$とします。
2次方程式のラグランジュ・リゾルベントは
$\alpha -\beta$
です。これは、
$x^2-1=0$の解$x=1, -1$
と$\alpha, \beta$で作られたのでした。
そして、これを2乗すると対称式となり、
対称式の基本定理から、基本対称式で表すことができます。
$(\alpha -\beta)^2=(\alpha +\beta)^2-4\alpha\beta$
です。
ここで、解と係数の関係から、
$\alpha +\beta =-\dfrac{b}{a}$
$\alpha\beta=\dfrac{c}{a}$
だったので、これを代入すると
$(\alpha -\beta)^2=\dfrac{b^2-4ac}{a^2}$
となり、
$\alpha +\beta=-\dfrac{b}{a}$
$\alpha -\beta =\pm \dfrac{\sqrt{b^2-4ac}}{a}$
の連立方程式で解の公式を求めたのでした。
次に3次方程式のラグランジュ・リゾルベントを考えます。
$ax^3+bx+cx+d=0$
の3つの解を$x=\alpha, \beta, \gamma$とします。
これと$x^3-1=0$の解$x=1, \omega, \omega^2$
を用いて作られる
$\alpha +\omega \beta +\omega^2 \gamma$
が3次方程式のラグランジュ・リゾルベントです。
3次方程式の場合はこれを三乗しても
3!=6通りの解の入れ替えで不変にならず、対称式になりませんでした。
しかし、解の入れ替わりで発生する式は
$(\alpha +\omega \beta +\omega^2 \gamma)^3$と
$(\alpha +\omega \gamma +\omega^2 \beta)^3$
の2つのみです。そこで、
$S^3=(\alpha +\omega \beta +\omega^2 \gamma)^3$
$T^3=(\alpha +\omega \gamma +\omega^2 \beta)^3$
とすると、$(S^3-T^3)^2$が対称式となり、
$\sqrt{(S^3-T^3)^2}$を求めてから$S^3, T^3$の三乗根をとることで
解の公式を得ることができると解明しました。
そして、今回は4次方程式が解ける仕組みに迫っていきます。
2次方程式・3次方程式についてのより詳細な解説は前回の記事をご覧ください。
4次方程式とラグランジュ・リゾルベント
ここでは、4次方程式をラグランジュ・リゾルベントを用いて考察していきますが、
それにあたって普通に4次方程式を解くやり方を知っておいた方が理解が深まるので、
概略だけ述べておこうと思います。
①$ax^3+bx^2+cx+d=0$の全体を$a$で割って最高次の係数を$1$にする
②平方完成っぽい変形で式を簡単にする
$y^4+Ay^2+By+C=0$の形になります
③$y=s+t+u$という置き換えをする
④色々置き換えつつ、3次方程式の解と係数の関係を発動し、
4次方程式を3次方程式に帰着させる
⑤3次方程式を解く
押さえて欲しいポイントは1つだけです。
4次方程式を上手いこと3次方程式に帰着させて解く
より詳細な解説は以下の記事をご覧ください

なぜ4次方程式を3次方程式に帰着させることができたのか?
これは偶然か?
それとも必然か?
ラグランジュ・リゾルベントを用いてその疑問の深部に迫っていきましょう。
まずは今までなんとなく使ってきたラグランジュ・リゾルベントの定義を確認します。
定義って大切です。
(定義:ラグランジュ・リゾルベント)
$n$次方程式
$a_nx^n+a_{n-1}x^{n-1}+\cdots a_1x+a_0=0$
の解を$x=x_1, x_2, \cdots, x_n$とする。
また、$\zeta_n=\cos \dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$
とする。このとき、
$x_1+\zeta_n x_2+\zeta_n^2 x_3+\cdots +\zeta_n^{n-1}x_n$
を$n$次のラグランジュ・リゾルベントという
※今回は$\zeta_n=\cos \dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$
を用いてラグランジュ・リゾルベントを定義しましたが、$\zeta_n$は
円分多項式$\Phi_n(x)$の解であれば何でもよいです。
4次方程式$ax^4+bx^3+cx^2+dx+e=0$
の4つの解を$x_1, x_2, x_3, x_4$とします。
定義に従って考えると、4次のラグランジュ・リゾルベントは
$x_1+\zeta_4x_2+\zeta_4^2 x_3+\zeta_4^3 x_4$
となります。
ラグランジュ・リゾルベントを用いて方程式を分析する際は、対称性が大切になります。
対称式をゲット
→対称式の基本定理発動
→対称式が基本対称式で表される
→解と係数の関係より、基本対称式は方程式の係数で表される
→対称式が方程式の係数で表される
→連立方程式で解が求まり、方程式が解ける
という流れで2次方程式・3次方程式は解ける仕組みを解明できました。
なので、4次方程式の場合も、
$x_1+\zeta_4x_2+\zeta_4^2 x_3+\zeta_4^3 x_4$
から出発して段々対称性を高めていく必要があります。
対称式とは、並び替えで不変な式のことです。
今回の場合は、4つの解$x_1, x_2, x_3, x_4$の並び替えで不変であるような式を作ることをまずは目指します。
並び替えは、全部で4!=24通りあります。
そこで、まずは
$x_1+\zeta_4x_2+\zeta_4^2 x_3+\zeta_4^3 x_4$
に24通りの並び替えを作用させてみましょう。
なにせ4次の場合は24通りも並び替えがあるので、
はっきり言って、3次の時とは次元が違うレベルで式変形が複雑です。
しかし、複雑なだけで、やっていること自体は全て対称性を高めているという一言に尽きます。
$L_1=x_1+\zeta_4x_2+\zeta_4^2 x_3+\zeta_4^3 x_4$
と表すことにし、並び替えを作用させたものを順に
$L_1, L_2, \cdots, L_{24}$としましょう。
結構大変ですが、まとめるとこうなります。
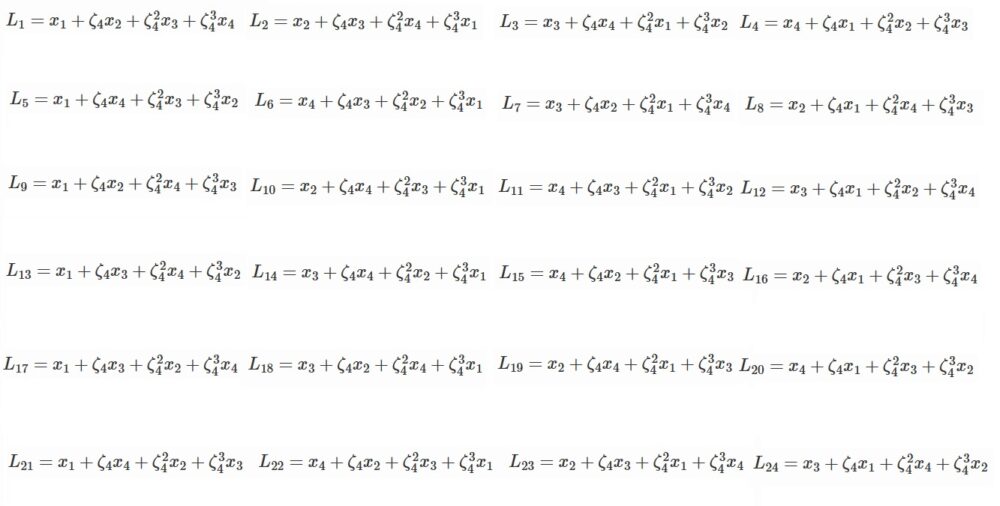
さて。
今までのことを振り返ってみましょう。
2次の場合は、$\alpha-\beta$を二乗して$(\alpha -\beta)^2$を得ることで対称性を高めました。
3次の場合は、$\alpha +\omega \beta +\omega^2\gamma$を三乗して$(\alpha +\omega \beta +\omega^2\gamma)^3$を得ることで対称性を高めました。
この流れでいくと、
4次の場合は
$L_1=x_1+\zeta_4x_2+\zeta_4^2 x_3+\zeta_4^3 x_4$
を4乗しそうなものですが、
その前に少し立ち止まって考えるべきことがあります。
2次・3次の場合と4次の場合では、明らかに異なることがあるのです!
それは、4が素数ではないという点。
これは特筆に値すべき大きな違いです。
問題は、この違いがどこに聞いてくるか。
それは、$\zeta_4, \zeta_4^2, \zeta_4^3$
を見れば分かります。
4は素数ではないので、この中に原始4乗根ではないやつがいます。
円分多項式$\Phi_4(x)$の解にならないやつです!
$\zeta_4, \zeta_4^2, \zeta_4^3$なんて仰々しい書き方をしていると分かりにくいかもしれませんが、
$\zeta_4=i$です。
$\zeta_4, \zeta_4^2, \zeta_4^3$は、$i, i^2, i^3$のことです。
$i^2=-1$でしたね。これが犯人です。
$L_1=x_1+\zeta_4x_2+\zeta_4^2 x_3+\zeta_4^3 x_4$
を書き直すと、
$L_1=x_1+x_2i-x_3-x_4i$
$=(x_1-x_3)+(x_2-x_4)i$
となります。
つまり、
$L_1=(x_1-x_3)+(x_2-x_4)i$です。
この書き方で先ほどの並び替えの結果を書き直してみましょう。
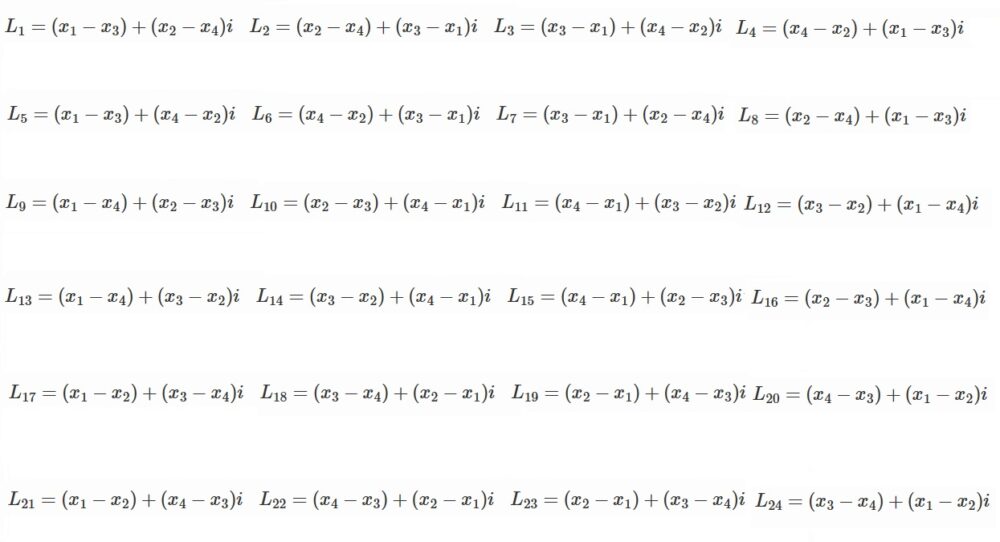
どうですか?
すでに結構対称性高くないですか?
例えば、$L_1$ と $L_5$ を見てください

$L_1=(x_1-x_3)+(x_2-x_4)i$
$L_5=(x_1-x_3)+(x_4-x_2)i$
ほぼ同じです!
もう少し見やすくすると、
$L_1=(x_1-x_3)+(x_2-x_4)i$
$L_5=(x_1-x_3)-(x_2-x_4)i$
どうですか?
これなら、4乗するより前に2乗したくなりませんか?
$(L_1)^2=(x_1-x_3)^2+2(x_1-x_3)(x_2-x_4)-(x_2-x_4)^2$
$(L_5)^2=(x_1-x_3)^2-2(x_1-x_3)(x_2-x_4)-(x_2-x_4)^2$
この2つの式を見たら、足したくなるのが人情というものです。
真ん中の項が消えます。
$(L_1)^2+(L_5)^2=2(x_1-x_3)^2-2(x_2-x_4)^2$
となります。
さらに、右隣の$L_2$ と $L_6$ のペアでも同じことを考えてみます
$(L_2)^2+(L_6)^2=2(x_2-x_4)^2-2(x_1-x_3)^2$
となります。ヤバくないですか?
符号が違うだけです!!
すなわち、
$(L_2)^2+(L_6)^2=-\lbrace (L_1)^2+(L_5)^2 \rbrace$
が成立するということです。
ということは、両辺を2乗すれば、
$\lbrace (L_1)^2+(L_5)^2 \rbrace^2=\lbrace (L_2)^2+(L_6)^2 \rbrace^2$
となります。横にスライドしつつ同じ作業を繰り返していくと、
$\lbrace (L_1)^2+(L_5)^2 \rbrace^2=\lbrace (L_2)^2+(L_6)^2 \rbrace^2=\lbrace (L_3)^2+(L_7)^2 \rbrace^2=\lbrace (L_4)^2+(L_8)^2 \rbrace^2$
となります。
そして、同様のことが下に並んでいるやつらでも起こります。
すなわち、
$\lbrace (L_9)^2+(L_{13})^2 \rbrace^2=\lbrace (L_{10})^2+(L_{14})^2 \rbrace^2=\lbrace (L_{11})^2+(L_{15})^2 \rbrace^2=\lbrace (L_{12})^2+(L_{16})^2 \rbrace^2$
$\lbrace (L_{17})^2+(L_{21})^2 \rbrace^2=\lbrace (L_{18})^2+(L_{22})^2 \rbrace^2=\lbrace (L_{19})^2+(L_{23})^2 \rbrace^2=\lbrace (L_{20})^2+(L_{24})^2 \rbrace^2$
となります。
かなり対称性が高まってきています。

最初は24個の並べ替えでバラバラになっていましたが、今や行き先は3つのみです。
例えば、
$\lbrace (L_1)^2+(L_5)^2 \rbrace^2$は対称式ではありませんが、
上の図の青いやつらに対応する8つの並べ替えでは不変です。
同様に、$\lbrace (L_9)^2+(L_{13})^2 \rbrace^2$は
上の図の赤いやつらに対応する8つの並べ替えで不変で、
$\lbrace (L_{17})^2+(L_{21})^2 \rbrace^2$は
上の図の緑のやつらに対応する8つの並び替えで不変です。
$\lbrace (L_1)^2+(L_5)^2 \rbrace^2$と$\lbrace (L_9)^2+(L_{13})^2 \rbrace^2$と$\lbrace (L_{17})^2+(L_{21})^2 \rbrace^2$
そう。今残っている式は3つです。
これが4次方程式を3次方程式に帰着できた理由です!!
ここまで来たら、あとは3次方程式と同じ議論で解を求めるところまで一直線!
式を簡略化するため、
$\lbrace (L_1)^2+(L_5)^2 \rbrace^2=A$
$\lbrace (L_9)^2+(L_{13})^2 \rbrace^2=B$
$\lbrace (L_{17})^2+(L_{21})^2 \rbrace^2=C$
と置くことにします。
そして、$A, B, C$を用いて3次のラグランジュ・リゾルベントを新たに作って3乗し、
$S^3=(A+\omega B+\omega^2 C)^3$
$T^3=(A+\omega C+\omega^2 B)^3$
とすると、
$(S^3-T^3)^2$が対称式となります。
ここで、対称式の基本定理より、これは
$x_1, x_2, x_3, x_4$の基本対称式で表されます。
さらに、解と係数の関係より、この基本多少式はそれぞれ
4次方程式の係数$a, b, c , d ,e$で表されます。
そこで、
$(S^3-T^3)^2=D$と置きます。 ($D$は$a, b, c, d, e$で表されている)
$S^3-T^3=\pm \sqrt{D}$
です。
また、$S^3+T^3$も対称式となっているので、
$S^3+T^3=E$と置きます。 $(Eはa, b, c, dで表されている)$
$S^3+T^3=E$
$S^3-T^3=\pm \sqrt{D}$
を解くと、
$S^3, T^3$
が$a, b, c, d, e$と平方根で表されることになります。
$S^3=F, T^3=G$
と置き、三乗根をとると
$S$ と $T$ が$a, b, c, d$と平方根と三乗根で表されることにまります。
そこで、
$S=s, T=t$ $s, tはa, b, c, dと平方根と三乗根で表されている$
と置くことにしましょう。
$A+\omega B+\omega^2C=s$
$A+\omega C+\omega^2B=t$
です。
ここで、
$A+B+C=\lbrace (L_{1})^2+(L_{5})^2 \rbrace^2+\lbrace (L_{9})^2+(L_{13})^2 \rbrace^2+\lbrace (L_{17})^2+(L_{21})^2 \rbrace^2$
を考えてみると、これも$x_1, x_2, x_3, x_4$の対称式であることに気づきます。
対称式の基本定理と解と係数の関係のコンボより、
$A+B+C$は$a, b, c, ,d, ,e$で表すことができるので、
$A+B+C=u$ ($u$は$a, b, c, d, e$で表されている)と置きます。
まとめると、
$A+B+C=u\cdots ㋐$
$A+\omega B+\omega^2C=s\cdots ㋑$
$A+\omega C+\omega^2B=t\cdots ㋒$
です。
㋐+㋑+㋒をします。
$3A+(1+\omega +\omega^2)B +(1+\omega^2+\omega)C=u+s+t$
となり、$\omega^2+\omega +1=0$
から
$3A =u+s+t$
$A =\dfrac{1}{3} (u+s+t)$
$B$については、
$㋐+㋑×\omega^2+㋒×\omega$より、
$B=\dfrac{1}{3}(u+\omega^2s+\omega t)$
と求まり、$C$は
$㋐+㋑×\omega + ㋒×\omega^2$より、
$C=\dfrac{1}{3}(u+\omega s+\omega^2 t)$
と求まります。
ここからラストスパートです。
いま、$A$は$s, t, u, \omega$で表されています。
$\lbrace (L_1)^2+(L_5)^2 \rbrace^2=A$
よって、
$(L_1)^2+(L_5)^2=\pm \sqrt{A}$
です。
新たにこれを$V$と置きましょう。
同様に、$\pm \sqrt{B}$を$W$とし、$\pm \sqrt{C}$を$Z$とします。
すると、
$(L_1)^2+(L_5)^2 =V$
$(L_9)^2+(L_{13})^2 =W$
$(L_{17})^2+(L_{21})^2 =Z$
です。これを書き下していきましょう。
$(x_1-x_3)^2-(x_2-x_4)^2=V$
$(x_1-x_4)^2-(x_2-x_3)^2=W$
$(x_1-x_2)^2-(x_4-x_3)^2=V$
この3つの式の左辺を展開していきます。
$x_1^2-2x1x_3+x_3^2-x_2^2+2x_2x_4-x_4^2=V\cdots ㋓$
$x_1^2-2x_1x_4+x_4^2-x_2^2+2x_2x_3-x_3^2=W\cdots ㋔$
$x_1^2-2x_1x_2+x_2^2-x_4^2+2x_4x_3-x_3^2=Z\cdots ㋕$
㋓+㋔+㋕より
$3x_1^2-2(x_2+x_3+x_4)x_1-(x_2^2+x_3^2+x_4^2)+2(x_2x_3+x_3x_4+x_4x_2)=V+W+Z$
さて。あとはこの2次方程式を解けば$x_1$が求まってすべての戦いが終わりそうですが、
係数と定数項に$x_2, x_3, x_4$が残ってしまっているのが問題です。
$x_2, x_3, x_4$を消去する方法はないでしょうか?
実はあります!
元々の4次方程式
$ax^4+bx^3+cx^2+dx+e=0$
を思い出しましょう。これの解と係数の関係を発動します。
$x_1+x_2+x_3+x_4=-\dfrac{b}{a}$
$x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_3x_4+x_4x_2=\dfrac{c}{a}$
$x_1x_2x_3+x_2x_3x_4+x_3x_4x_1+x_4x_1x_2=-\dfrac{d}{a}$
$x_1x_2x_3x_4=\dfrac{e}{a}$
でした。
この最初の式と2番目の式に着目します。
$x_1+x_2+x_3+x_4=-\dfrac{b}{a}$
より、
$x_2+x_3+x_4=-\dfrac{b}{a}-x_1\cdots ㋖$
$x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4=\dfrac{c}{a}$より、
$x_2x_3+x_3x_4+x_4x_2=\dfrac{c}{a}-(x_2+x_3+x_4)x_1\cdots ㋗$
ここで、
$3x_1^2-2(x_2+x_3+x_4)x_1-(x_2^2+x_3^2+x_4^2)+2(x_2x_3+x_3x_4+x_4x_2)=V+W+Z$
に㋖と㋗を代入して整理しましょう。
$3x_1^2-2(-\dfrac{b}{a}-x_1)x_1-(x_2^2+x_3^2+x_4^2)+2\lbrace \dfrac{c}{a}-(x_2+x_3+x_4)x_1\rbrace=V+W+Z$
さらに㋖を代入しましょう。
$3x_1^2-2(-\dfrac{b}{a}-x_1)x_1-(x_2^2+x_3^2+x_4^2)+2\lbrace \dfrac{c}{a}-(-\dfrac{b}{a}-x_1)x_1\rbrace=V+W+Z$
ここで、$x_2^2+x_3^2+x_4^2=(x_2+x_3+x_4)^2-2(x_2x_3+x_3x_4+x_4x_2)$
であったことを思い出し、整理すると、最終的には$x_2, x_3, x_4$は消去されて、
$x_1$についての2次方程式が出来上がります。(思ったより式がヤバかったので、係数は省略します)
この2次方程式を$kx_1^2+lx_1+m=0$
とします。
$kx_1^2+lx_1+m=0$ を解けば$x_1$が求まります。
めでたしめでたし。
体(たい)で捉えなおす
ここまでの流れを整理しましょう。
まずは4次のラグランジュ・リゾルベント
$L_1=(x_1-x_3)+(x2-x_4)i$
を作りました。
これに4!=24通りの並び替えを適応すると、
$L_1, L_2, \cdots, L_{24}$
が誕生しました。
対称性を高めるため、
まず$(L_1)^2+(L_5)^2$をしました。
さらに、これを二乗して、
$\lbrace (L_2)^2+(L_5) \rbrace^2$
まで対称性を高めると、並び替えで発生する式がちょうど3個になります
これら3個の式を用いて3次のラグランジュ・リゾルベントをつくり、それを3乗すると
$(S^3-T^3)^2$が対称式になって対称の基本定理&解と係数の関係のコンボで
方程式の係数で表されることになります。
そして、最終的に$x_1$についての2次方程式
$kx_1^2+lx_1+m=0$
を解いて解までたどり着けることを確認しました。
これを体を用いて捉えなおすと以下のようになります
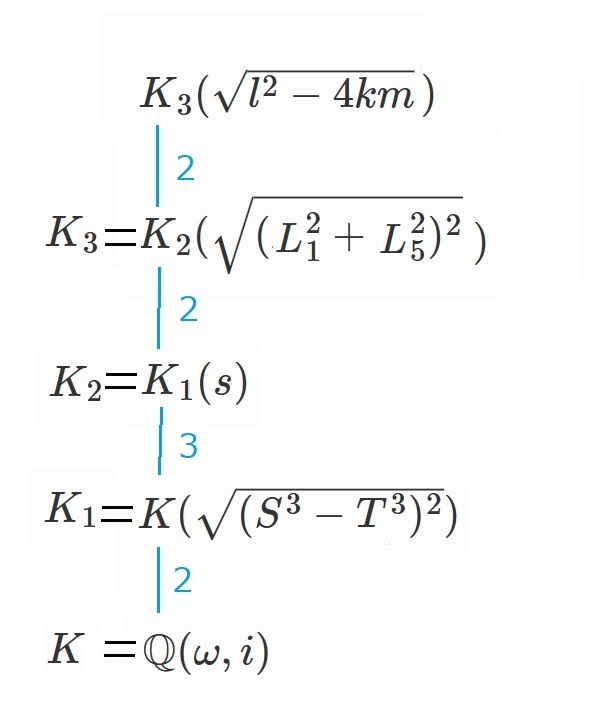
青色の数字には結構深い意味があるのですが、これは後々の記事のお楽しみとしておきましょう。
まとめ
・4次方程式が3次方程式に帰着できる理由もラグランジュ・リゾルベントで説明できた
・4は素数ではないので、もともと少しだけ対称性が高い
・故にいきなり4乗せず、まず2乗する
次回は$x^n-1=0$が代数的に解けることを示していきたいと思います。
ご期待ください。
参考
画像素材提供(アイキャッチ):Gerd AltmannによるPixabayからの画像

コメント
コメント一覧 (2件)
ラグランジュリゾルベントを用いての解法ですが、
結果的には最後の体の拡大の様子を表す図において、
有理数体にωだけを添加(結果的に原始4乗根の添加は不要)しておけばよいことになりますよね?
のもとさん
コメントありがとうございます。
その通りです。
有限次元分離拡大は全て単拡大という事実をまだ記事にしていなかったので
あんな感じの表記になっています。