正弦定理を円周角の定理を使って証明

今回は、数学Ⅰで習う正弦定理を円周角の定理を用いて証明します。

また、なぜ円周角の定理を使うのか、どうやってその発想にたどり着くか、

といった思考回路も合わせて解説します。

正弦定理とは？

「$⊿ABC$について、$AB=c, BC=a, CA=b, $外接円の半径を$R$としたとき、

$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$

が成立する。」

定理は数学における必殺技。

発動条件と、結果を分けて捉える必要があります。

今回は、緑マーカーが条件で、黄色マーカーが結果です。

証明

一応もう一度定理をかいておきます。

$⊿ABC$について、$AB=c, BC=a, CA=b, $外接円の半径を$R$としたとき、

$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$

が成立する。

～脳内会議～

定理を眺めるとき、第一着目ポイントは条件です。

緑マーカーの条件をよく眺めましょう。

ピックアップすべきキーワードが今回は２つあります。

「三角形」と「外接円」です。

まずは三角形とその外接円を描いてみましょう。

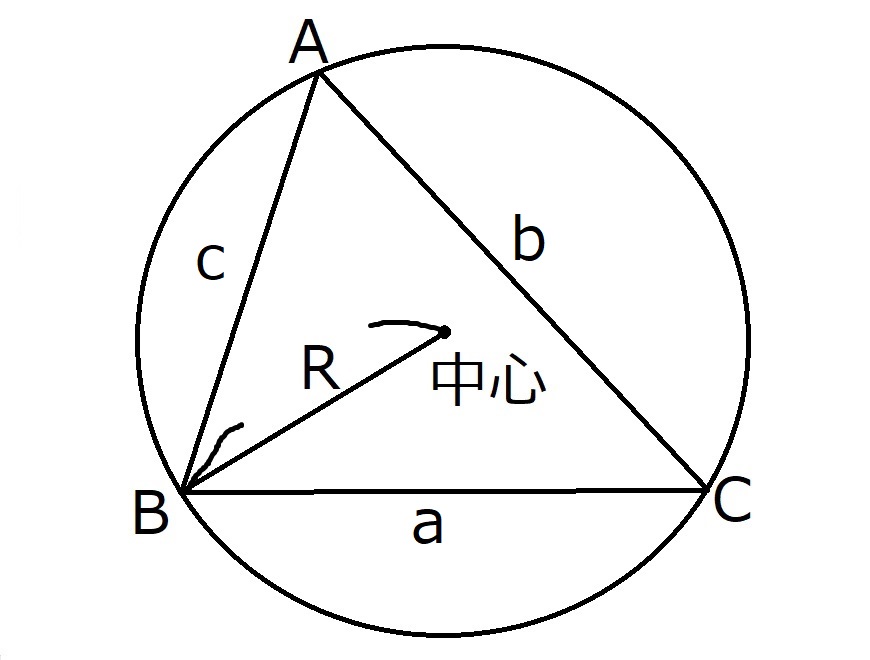
さて、これで条件から拾うべき情報は全て図に写し取ることができました。

次は結果である黄色マーカーに着目していきましょう。

まず注目すべきは、「サインが登場している」という点です。

先ほど書いた図に、どうにかしてサインを召喚しないといけません。

サインを召喚するために必要な呪文は３つありました。

①基準となる長さ

②角度$\theta$

③直角

このあたりのことがしっくりこない方は、こちらの記事をご覧ください。

先ほどの図にサインを召喚するため、

直角を見つける必要がある

ということを読み取ることができれば、ほぼ準備完了です。

さて、今回はキーワードとして「外接円」と「直角」が浮かび上がっています。

これらのことから次に何を思いつくかというと、

「直角・直径・円は３点セット」というテクニックです。

外接円の直径$2R$を補助線として書き込んで、直角を見つけ出せ！

というミッションを受信しましょう。

例えばこんな感じで直径を記入してみます。

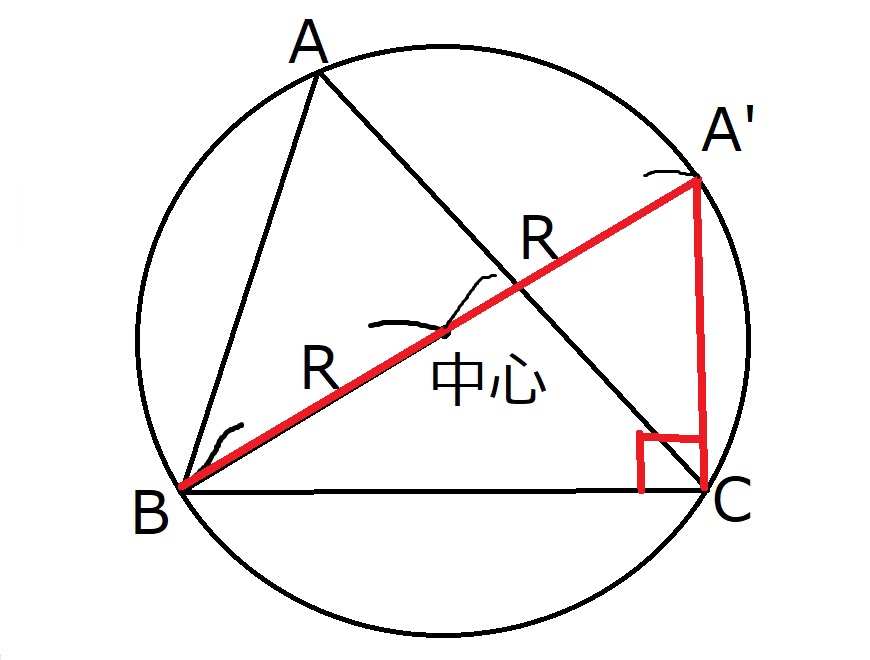
直角が見つかりました！

さて。

円周角の定理の発動条件が満たされていることにお気づきでしょうか？

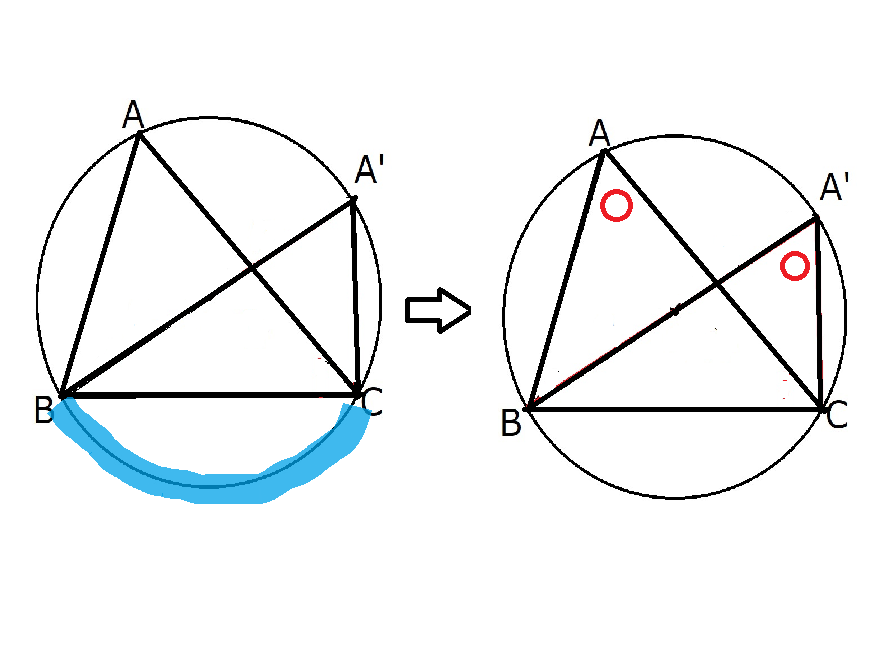
同じ弧に対する円周角が見つかったから、円周角の定理を発動するのです！

なお、補足ですが、ここまでの説明では三角形は鋭角三角形として考えています。

なぜなら、ウルトラマン式のサインの定義では、角の大きさが９０°までの場合しか有効でないからです。

しかし、三角形は当然のことながら鈍角三角形もあり得ますし、その場合も問題なく正弦定理は成立します。

以上のことから、証明の際は、鋭角三角形（すべての角が９０°より小さい）の場合と

鈍角三角形（９０°より大きい角がある）の場合で場合分けが必要になります。

ちなみに、鈍角の場合も基本的に発想は同じで、直径$2R$を補助線で書き出すことになります。

なお、証明の中で９０°を超える大きさの角についてサインが定義されていますが、

そこは一端目をつぶって、あ、定義できるんだな、と思ってください。

今後補足の記事を出します。

以上、脳内会議でした！

ここから証明に移っていきます！

～証明～

$i)$$⊿ABC$が鋭角三角形の場合。

$⊿ABC$の外接円の中心と頂点$B$を結んだ直線と、外接円との交点を$A’$とする。

下の図について、弧$BC$に対して円周角の定理より、

$∠BAC=∠BA’C＝A$

である。

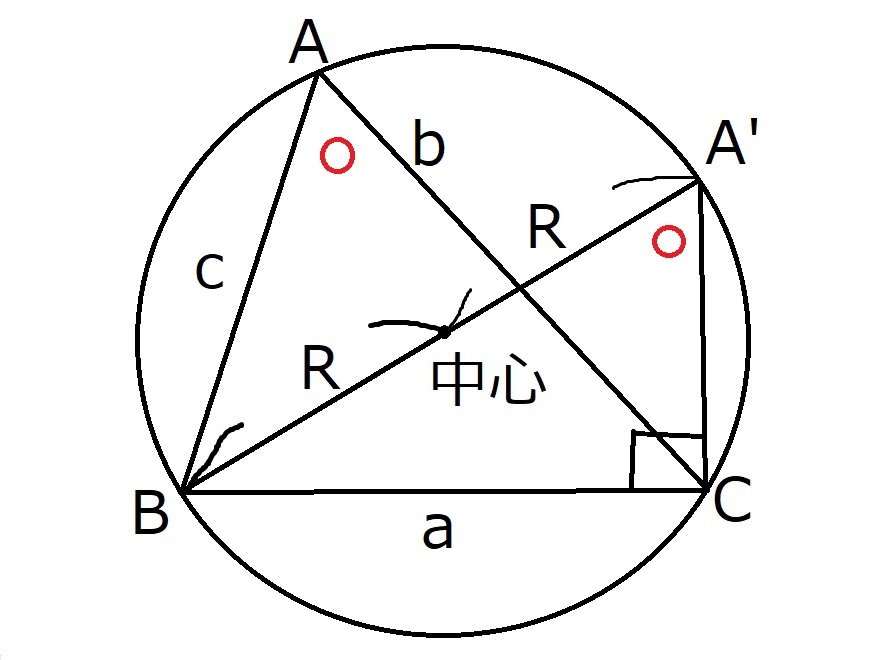
$⊿BCA’$を取り出し、頂点Bが上になるように向きを変える。

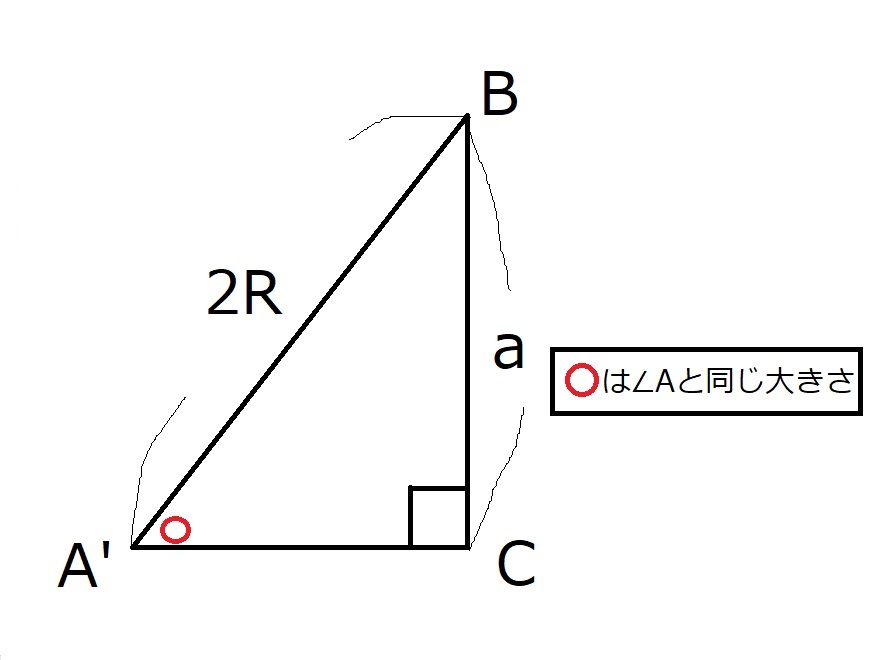
すると、$a=2R\sin A$であることが分かる。

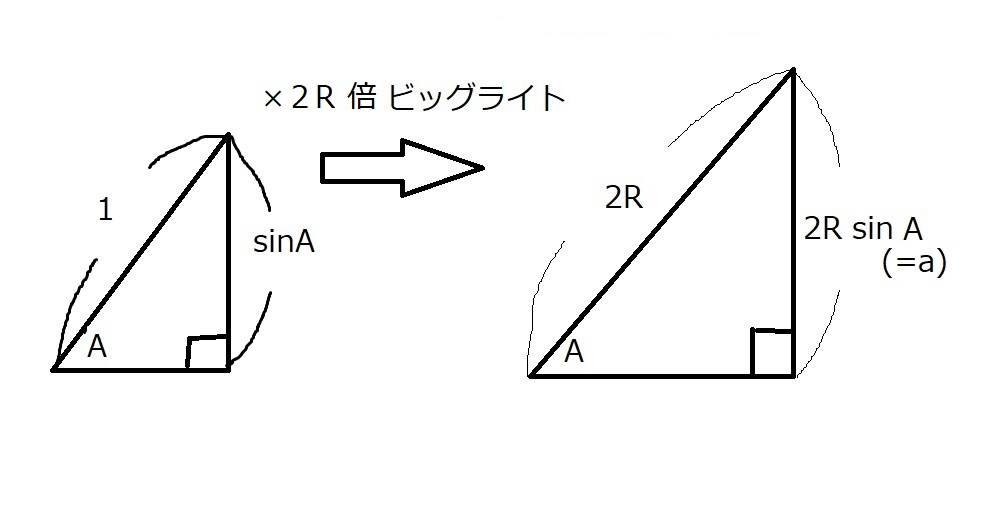
よって、$\dfrac{a}{\sin A}=2R$となる。

$∠B, ∠C$についても同様。

よって、

$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$

となる。

$ii)$$⊿ABC$が鈍角三角形の場合

$∠A$が鈍角であると考えても一般性を損なわない。

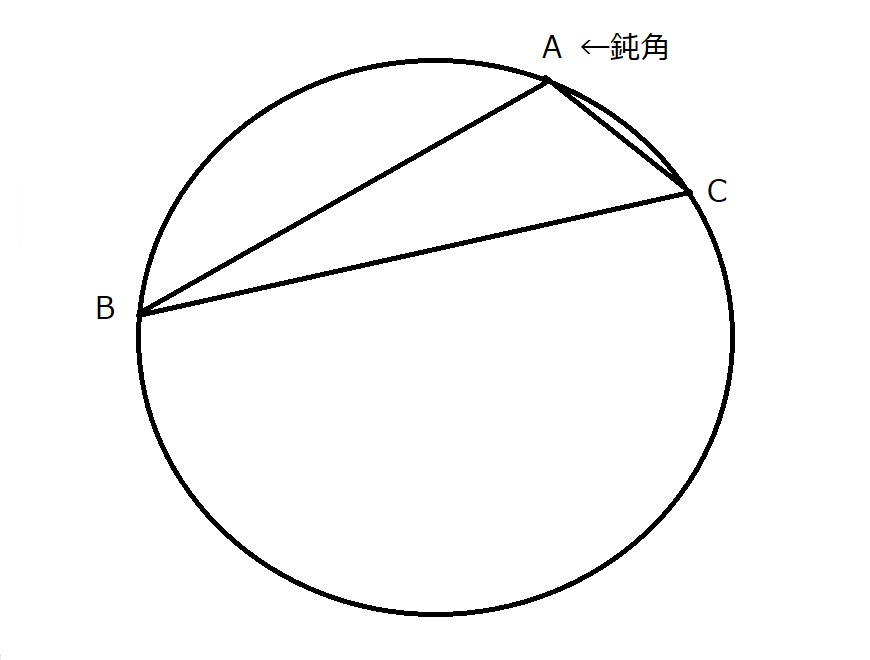
$∠Bと∠C$は鋭角なので、$i)$より、

$\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\cdots ①$

は成立。

ここで、頂点Bと外接円の中心を結んだ直線と、外接円の交点をA’とする。

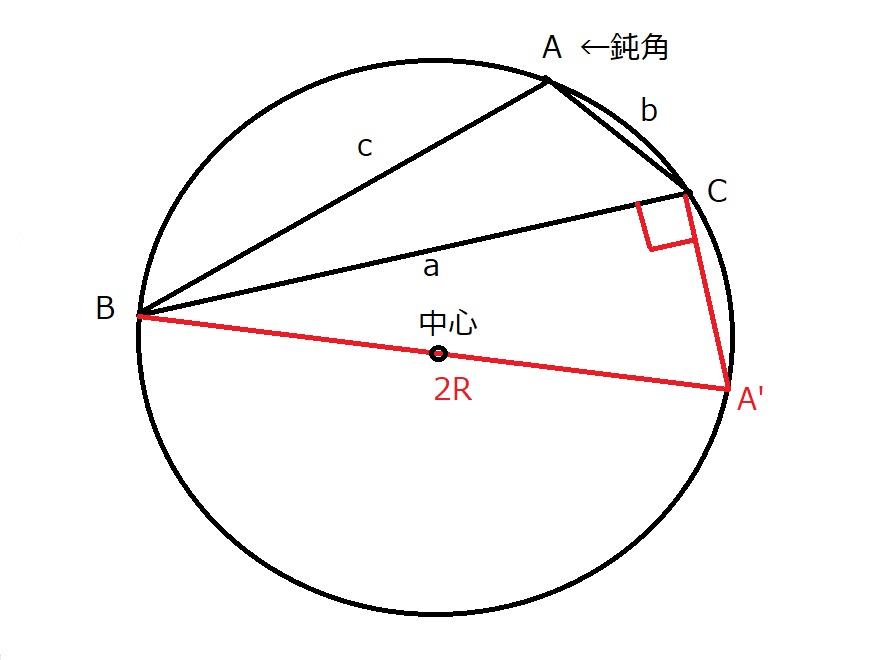
下の図において、四角形BACA’は円に内接する四角形である。

よって、向かい合う角の和は１８０°となるので、

$A＋A’＝１８０°$となり、

$A’=１８０°-A$である。

⊿BA’Cは鋭角三角形となるので、

$i)$より、

$\dfrac{a}{\sin A’}=2R$

となり、

$A’=１８０°-A$

を代入すると、

$\dfrac{a}{\sin (180°-A)}=2R$

となる。

ここで、$\sin (180°-A)=\sin A$であるので、←今は認めてください

$\dfrac{a}{\sin A}=2R \cdots ②$

①と②より、

$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$

である。

$i)$と$ii)$より、正弦定理は証明された。

（証明終了）

まとめ

いかがでしたか？

・公式の証明では条件と結果を分けて考える

・結果のサインに着目し、90°を探す

・直角・直径・円はワンセット

・同じ弧に対する円周角が出現したので、円周角の定理を使う

・サインの定義より、証明完了

この流れを押さえていただければと思います。

知識と知識を線で結ぶ作業のよりどころが、条件と結果です。

条件と結果を整理し、

自分の知っている定理の発動条件が満たされていたら使う。

この繰り返しが天才的（に見える）発想の原動力となります。

また次回の記事でお会いしましょう！