なんか紛らわしい公式を念仏のように覚えさせられるページ
それが三角関数の性質
覚えてはいけない
意味をよく考えれば、自然と出てくるから
公式一覧
今からヤバい式が沢山出てきます。
実に18個もありますので、
心の準備をしてくださいね。
ちなみに、覚える必要は全くないのでご安心を。
僕も覚えていません笑
でも使う場面は結構あります。
入試やテストでこれを使う場面がきたらどうするか?
答えは簡単。
つくればいいのです。
~$\dfrac{\pi}{2} シリーズ$~
1-1 $\sin (\dfrac{\pi}{2}-\theta)=\cos \theta$
1-2 $\cos (\dfrac{\pi}{2}-\theta)=\sin \theta$
1-3 $\tan (\dfrac{\pi}{2}-\theta)=\dfrac{1}{\tan \theta}$
~$\pi シリーズ$~
2-1 $\sin (\pi -\theta)=\sin \theta$
2-2 $\cos (\pi -\theta)=-\cos \theta$
2-3 $\tan (\pi-\theta)=-\tan \theta$
~$+ 2\pi シリーズ$~
3-1 $\sin (\theta + 2\pi)=\sin \theta$
3-2 $\cos (\theta +2\pi)=\cos \theta$
3-3 $\tan (\theta +2\pi)=\tan \theta$
~$+\pi シリーズ$~
4-1 $\sin (\theta + \pi)=-\sin \theta$
4-2 $\cos (\theta +\pi)=-\cos \theta$
4-3 $\tan (\theta +\pi)= \tan \theta$
~$+\dfrac{\pi}{2}シリーズ$~
5-1 $\sin (\theta +\dfrac{\pi}{2})=\cos \theta$
5-2 $\cos (\theta +\dfrac{\pi}{2})=-\sin \theta$
5-3 $\tan (\theta +\dfrac{\pi}{2})=-\dfrac{1}{\tan \theta}$
~$-\theta シリーズ$~
6-1 $\sin (-\theta)=-\sin \theta$
6-2 $\cos (-\theta)=\cos \theta$
6-3 $\tan (-\theta)=-\tan \theta$
1. $\dfrac{\pi}{2}シリーズの導出$
これは三角比の定義からほぼ一撃で出てきます。
定義の直角三角形をかいて、向きを変えます。
90°が$\dfrac{\pi}{2}$である点だけ注意してください
直角三角形の3つの角の大きさは、
$\theta, \dfrac{\pi}{2}, \dfrac{\pi}{2}-\theta$です。
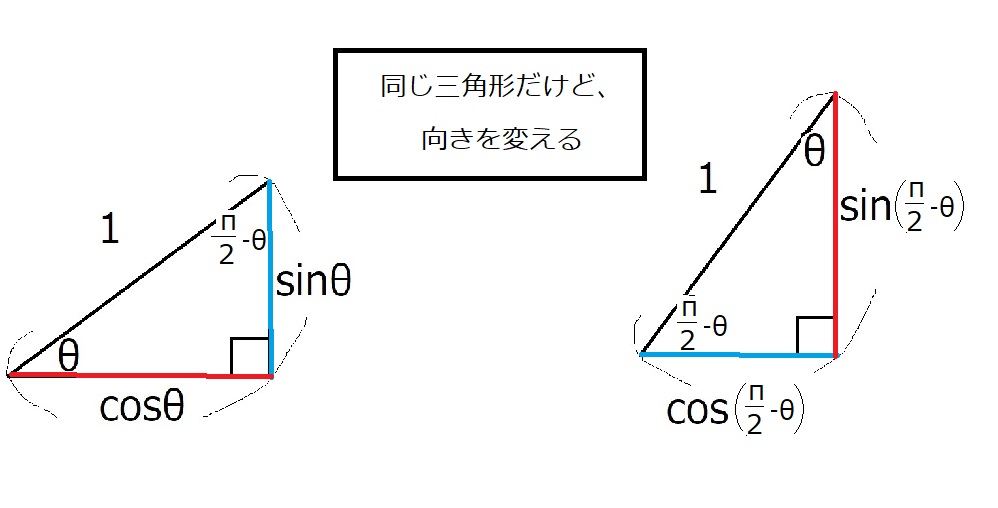
赤い辺の長さは等しいので、
$\sin (\dfrac{\pi}{2}-\theta)=\cos \theta$
青い辺の長さも等しいので、
$\cos (\dfrac{\pi}{2}-\theta)=\sin \theta$
タンジェントはちょい複雑です
$\tan (\dfrac{\pi}{2}-\theta)=\dfrac{あか}{あお}=\dfrac{\cos \theta}{\sin \theta}=\dfrac{1}{\tan \theta}$
となります。
2. $\pi シリーズの導出$
このシリーズは、$\pi -\theta$が単位円上のどこにいるか、
これだけ把握できればOKです。
あと、サインは縦の長さ、コサインは横の長さということも覚えていきましょう。
まず、単位円上の角度は、
反時計回りが正の向きです。
$\pi- \theta$は、
$\pi$から$\theta$だけ戻った点、と理解しましょう。
つまり、三角比の定義の直角三角形を逆向きに突っ込んだ位置にいます。
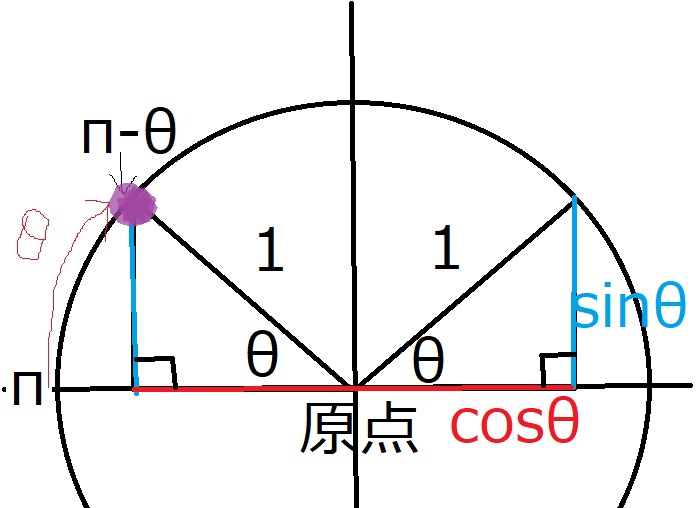
紫の点のたてが$\sin(\pi-\theta)$で、
よこが$\cos (\pi-\theta)$です。
一方、左右の三角形は合同です。
(直角三角形の斜辺と他の1つの角が等しい)
合同なので当然縦の長さ(青い辺)は等しくなり、
$\sin(\pi-\theta)=\sin \theta$です。
横の長さも等しいのですが、横については原点をまたいでしまっているので、
長さは等しいですが向きが逆です。
向きが逆、ということは、マイナスが付く、ということです。
よって$\cos(\pi-\theta)=-\cos \theta$となります。
タンジェントは傾きです。
左右の直角三角形の斜辺の傾きは、左右対称です。
右上がりか、右下がりかだけが違います。
よって、片方にマイナスをつけることになり、
$\tan(\pi -\theta)=-\tan \theta$
となります。
3. $+2\pi シリーズの導出$
これは全シリーズで一番簡単です。
$2\pi$が360°であることだけ思い出しておきましょう。
360°プラスしても、一周回って元に戻るので、位置は変わりません。
位置が変わらないので、たて・よこ・傾きも変わりません。
よって
$\sin (\theta + 2\pi)=\sin \theta$
$\cos (\theta +2\pi)=\cos \theta$
$\tan (\theta +2\pi)=\tan \theta$
4. $+\pi シリーズ$
$\pi$は180°と覚えておきましょう。
そして、180°は、つまり半周です。
$(\theta +\pi)$の位置だけ確認できればあとは簡単です。
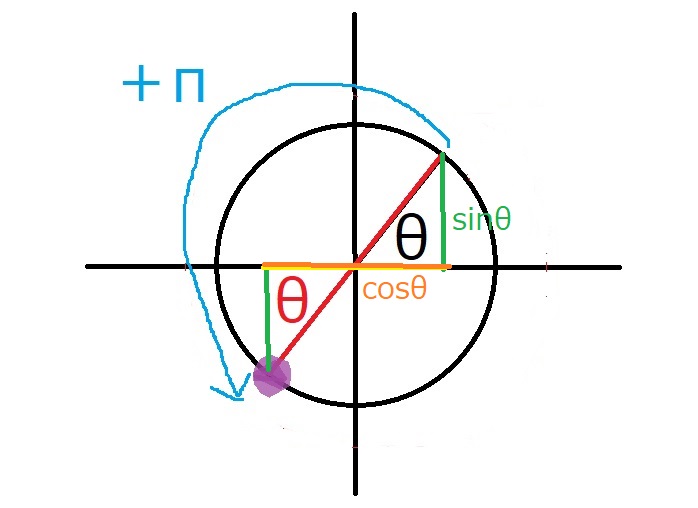
紫の点の$y$座標の値が$\sin(\theta +\pi)$で、
$x$座標の値が$\cos(\theta \pi)$です。
2つの三角形は合同なので、緑同士、オレンジ同士の長さは等しいです。
しかし、向きは逆ですので、マイナスをつけることになります。
よって、
$\sin (\theta + \pi)=-\sin \theta$
$\cos (\theta +\pi)=-\cos \theta$
となります。
そして、タンジェントは傾きですが、
2つの三角形の赤い直線は共通ですので、傾きに変化はありません。
$\tan (\theta +\pi)=\tan \theta$
です。
5. $+\dfrac{\pi}{2}シリーズ$
これだけはちょい難です。
でも結局$(\theta +\dfrac{\pi}{2})$の位置が分かればOKです。
$\dfrac{\pi}{2}$は90°なので、90°回転です!
半円を考えてください。
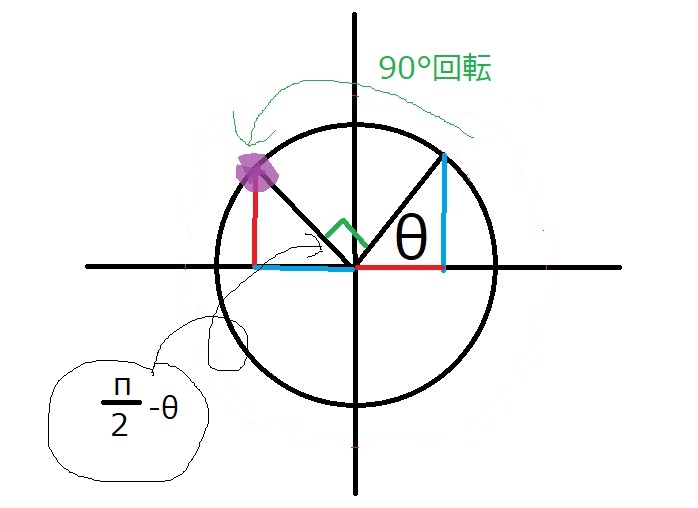
まず、$\theta$がいます。
そこから90°($\dfrac{\pi}{2}$)回転します。
すると、$\pi – (\theta +\dfrac{\pi}{2})=\dfrac{\pi}{2}-\theta$だけ残ります。
つまり、定義の直角三角形を向きを変えてはめ込んだところに紫の点はいます。
紫の点の$x$座標が$\cos (\theta +\dfrac{\pi}{2})$で、
$y$座標が$\sin (\theta +\dfrac{\pi}{2})$です。
赤い長さは$\cos \theta$
青い長さは$\sin \theta$です。
あとは、プラスなのかマイナスなのか読み取ります。
紫の点は$x$軸より上にいるので、縦の値はプラス、
横の値は、原点よりも左にいるのでマイナスです。
$\sin (\theta +\dfrac{\pi}{2})=\cos \theta$
$\cos (\theta+\dfrac{\pi}{2})=-\sin \theta$
です。
$\tan (\theta +\dfrac{\pi}{2})=\dfrac{\sin (\theta +\dfrac{\pi}{2})}{\cos (\theta+\dfrac{\pi}{2})}$
$=\dfrac{\cos \theta}{-\sin \theta}=-\dfrac{1}{\tan \theta}$
6. $-\theta$シリーズ
単位円で角の大きさを考えるとき、
反時計回りがプラス、時計回りがマイナスということだけ覚えておきましょう。
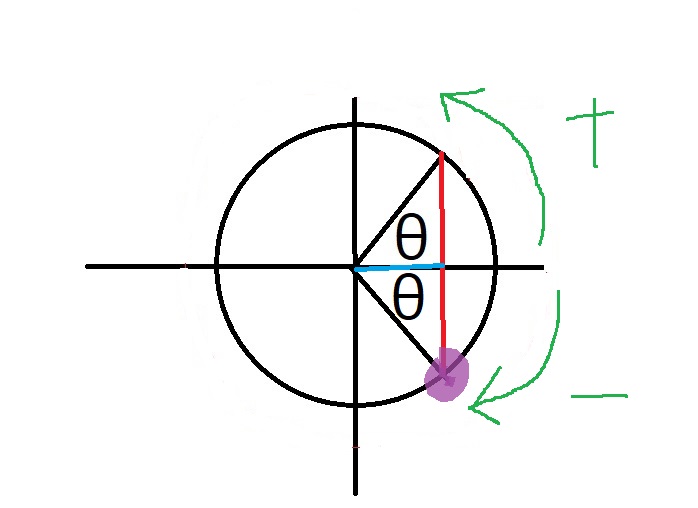
紫の点の$x$座標が$\cos (-\theta)$で、$y$座標が$\sin (-\theta)$です。
赤い長さは$\sin \theta$
青い長さは$\cos \theta$です。
紫の点は縦は下向きなのでマイナス、
横はそのままプラスです。
$\sin (-\theta)=-\sin \theta$
$\cos (-\theta)=\cos \theta$
$\tan (-\theta) =\dfrac{\sin (-\theta)}{\cos (-\theta)}=-\tan\theta$
です。
まとめ
いかがでしたか?
公式覚えなくてもその場で作ればなんとかなりそうだな、
と思っていただければ幸いです。
また次の記事でお会いしましょう!

コメント