加法定理の証明は、東大の2次試験でも出題されたことがあるくらい重要な内容です。
今回は、そんな加法定理の証明を紹介します。
この記事のほかにも、今後色々な別解を紹介していこうと思うので、
気に入ったやり方で証明をマスターしてください。
加法定理とは?
加法定理は、サインとコサインとタンジェントがあります。
$\sin (\alpha +\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta$
$\cos (\alpha +\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta$
$\tan (\alpha +\beta)=\dfrac{\tan \alpha +\tan \beta}{1-\tan \alpha \tan \beta}$
あと、それぞれに$(\alpha – \beta)$バージョンがあります。
三角比による証明
$\sin (\alpha +\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta$
を示します。
証明で大切なのは、条件と定義です。
今回は、特にピックアップすべき条件はないので、
$\sin (\alpha +\beta)$の定義が証明のよりどころとなります。
三角比流(ウルトラマン流)の定義を採用しましょう。
ウルトラマン流の三角比の定義という訳の分からないフレーズに違和感がある方は、
以下の記事をご覧ください。

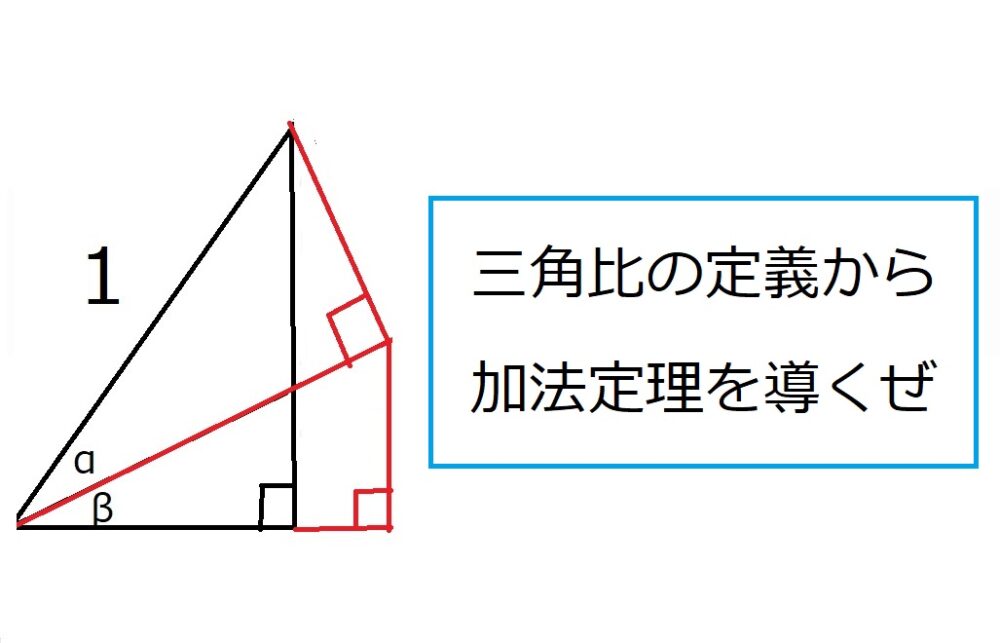
まずは、$\sin (\alpha +\beta)$を定義に従って図示する必要があります。
斜辺の長さが1の直角三角形をかきましょう。
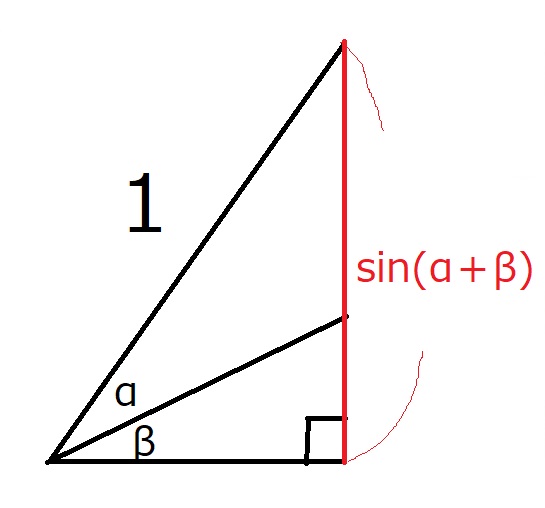
この縦の長さ(赤いところ)を
$\sin \alpha , \sin \beta, \cos \alpha ,\cos \beta$で表せ、
というのが今回のアウトラインです。
まず、図に$\sin \alpha , \sin \beta, \cos \alpha ,\cos \beta$
を登場させないといけません。
サインを召喚するのに必要な呪文は3つでした。
①基準となる長さ1
②角度
③直角
例えば、$\sin \alpha$を召喚しようと思ったら、
長さ1と角度$\alpha$はいますが、
いい感じの位置に直角がないです。
そこで、補助線で直角をつくります。
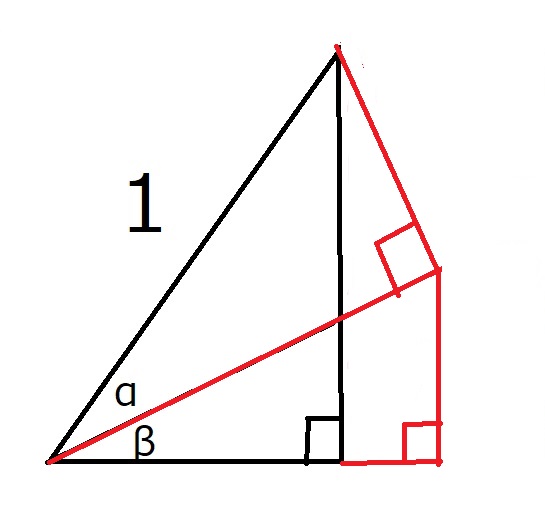
(証明)
$\sin (\alpha +\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta$
を示す。
斜辺の長さが1で、一つの鋭角が$(\alpha + \beta)$である直角三角形$ABC$を考える。
$AC=\sin(\alpha +\beta)$である。
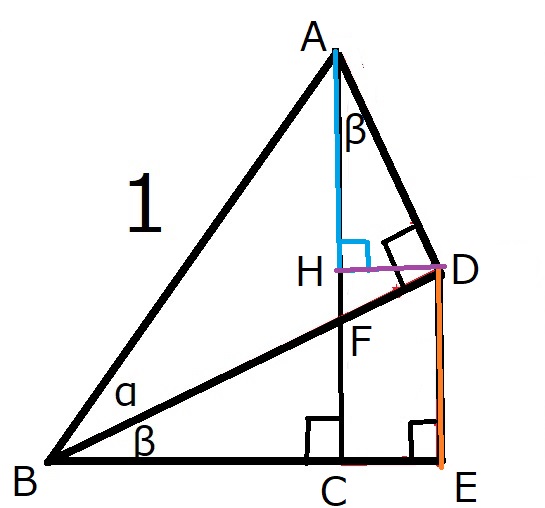
三角形ABCについて、$∠ABD=\alpha$となるように直線を引き、
その直線に向かって頂点$A$から下した垂線の足を$D$とする。
点$D$から直線$BC$に下した垂線の足を$E$とする。
線分$AC$と$BD$の交点を$F$とする。
また、点$D$から線分$AC$に下した垂線の足を$H$とする。
$⊿FBC$と$⊿FAD$は、3つの角の大きさが等しいので相似である。
よって、$∠FBC=∠FAD=\beta$となる。
いま、$AC=AH+DE \cdots ①$である。
ここで、$⊿ABD$について、
三角比の定義より、$DA=\sin \alpha$であり、
$BD=\cos \alpha$
である。
ここで、$⊿DAH$を考える。
三角比の定義より、
$AH=\sin \alpha \cos \beta $となる。
ここで、$⊿DBE $を考える。
$DB=\cos \alpha$である。
$⊿ DBE$について考える。
三角比の定義より、
$DE= \cos \beta \sin \alpha$である。
これらを①の式に代入
$\sin (\alpha +\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta$
(証明終了)
コサインの方もついでにやっときますか。
先ほどの図をもう一度使います。
(証明)
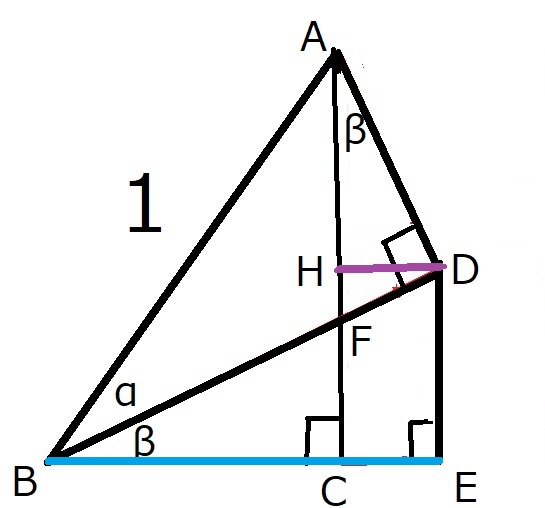
三角比の定義より、$BC=\cos (\alpha +\beta)$であり、
$BC=BE(青)-DH(紫)$
である。
ここで、$⊿ABD$について、三角比の定義より、
$BD=\cos \alpha, DA=\sin \alpha$
である。
次に$⊿DBE$を考える。
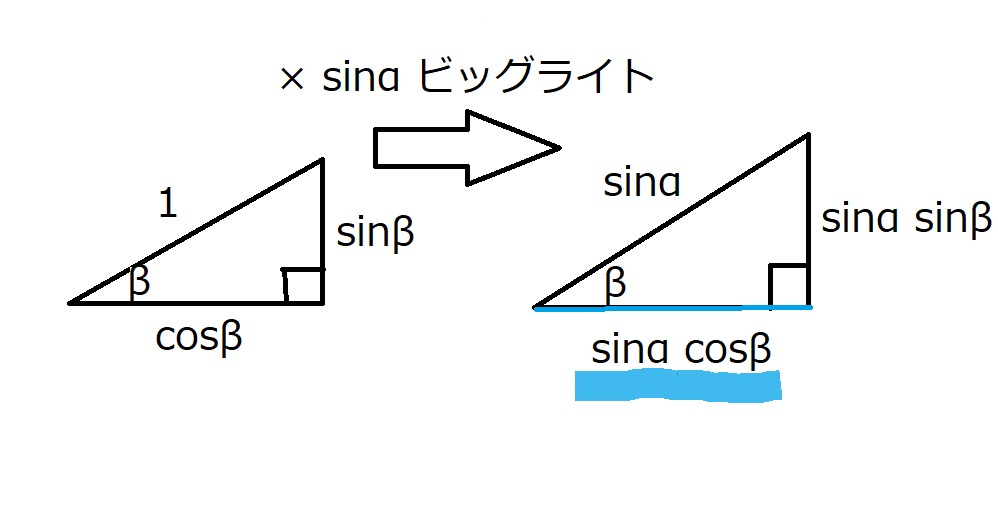
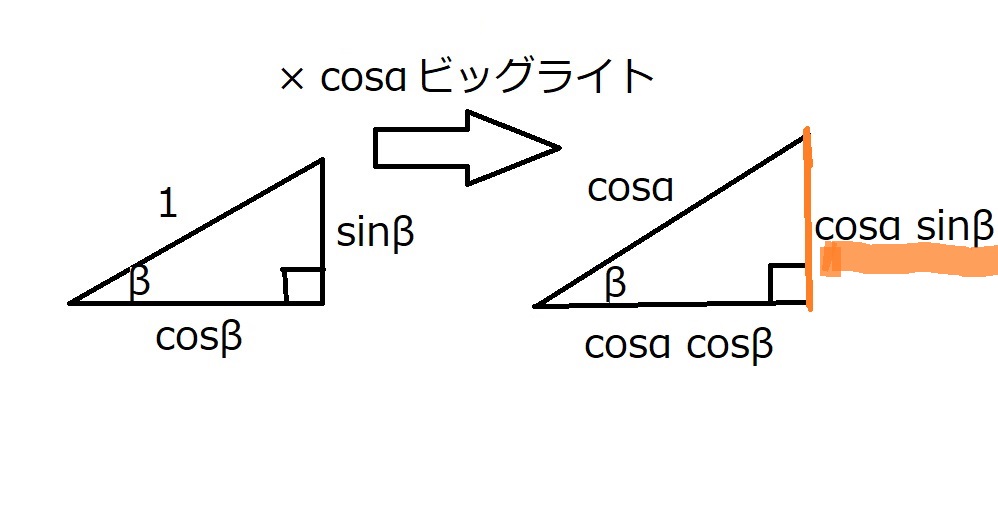
三角比の定義(×$\cos \alpha $ビッグライト)より、
$BE=\cos \alpha \cos \beta$ である。
ここで$⊿DAH$について、
三角比の定義より(×$\sin \alpha$ビッグライト)より、
$DH=\cos \alpha \cos \beta$である。
$BC=\cos (\alpha +\beta)$に注意し、
$BC=BE(青)-DH(紫)$にこれらを代入すると、
$\cos (\alpha +\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta$
となる。
(証明終了)
最後にタンジェントです。
(証明)
$\tan (\alpha +\beta)=\dfrac{\sin (\alpha +\beta)}{cos (\alpha +\beta)}$
$=\dfrac{\sin \alpha \cos \beta +\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \cos \beta}$
ここで、分子分母を$\cos \alpha \cos \beta$で割る。
$\tan (\alpha +\beta)=\dfrac{\dfrac{\sin \alpha}{\cos \alpha}+\dfrac{\sin \beta}{\cos \beta}}{1-\dfrac{\sin \alpha}{\cos \alpha} \dfrac{\sin \beta}{\cos \beta}}$
$=\dfrac{\tan \alpha +\tan \beta}{1-\tan \alpha \tan \beta}$
まとめ
いかがでしたか?
今回は三角比の定義に基づいて加法定理を証明しました。
加法定理の証明はいくつも別解がありますが、
僕は今回のやり方が一番好きです。
しかし、この証明はサインとコサインの定義でウルトラマン流を採用しているので、
$(\alpha +\beta)$が鋭角の場合しか作動しません。
鈍角の場合も含めた証明をするには、余弦定理を用います。
それはまた別の記事にまとめますので、ご期待ください。
ではまた次の記事でお会いしましょう!
コメント