三角関数が待っている。
さぁ行こう!
ウルトラマンポーズの向こう側へ!!
三角比のおさらいと、三角関数の定義
まずは三角比のおさらいから。
サインやコサインは、ウルトラマンポーズで定義されます。
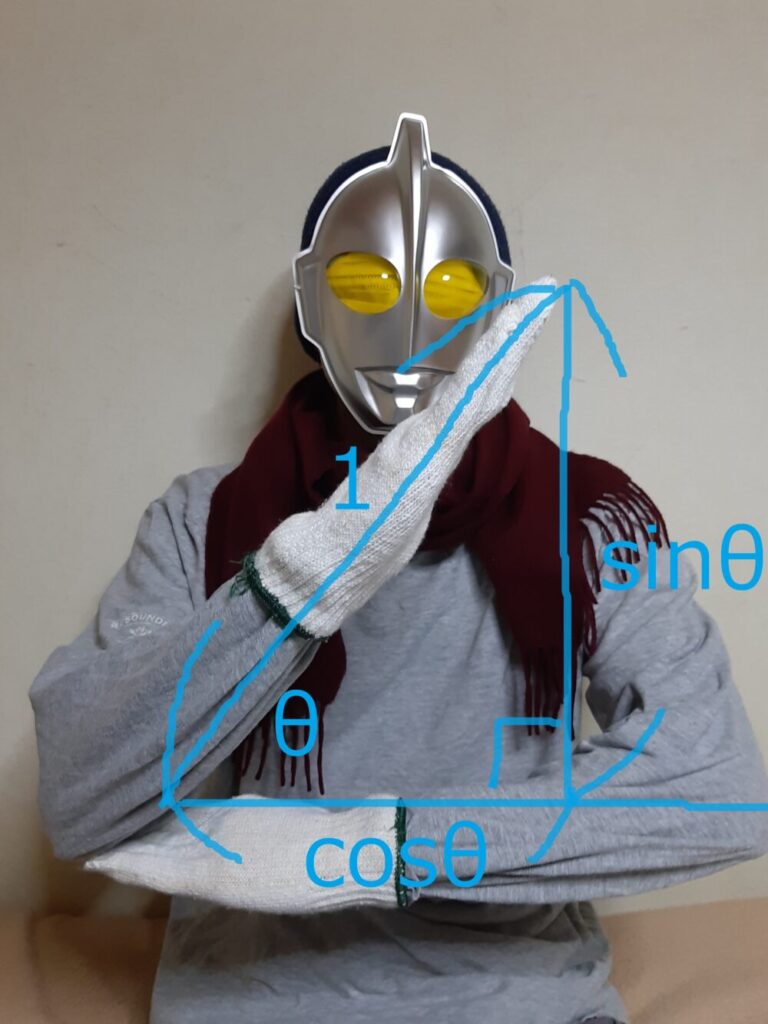
斜辺の長さが1の直角三角形について、
縦の長さがサイン、横の長さがコサイン
でした
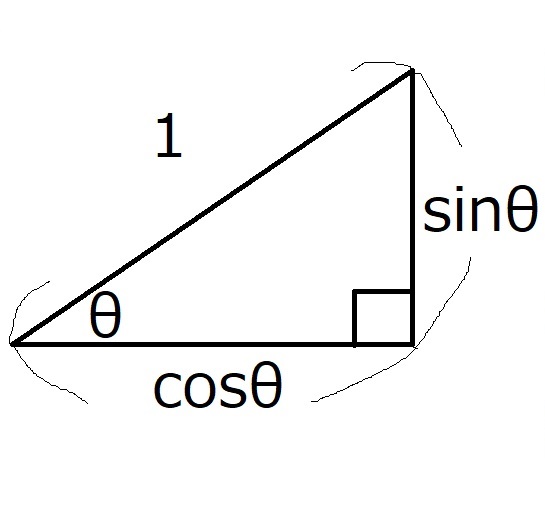
詳しくはこちらをご覧ください。

この定義の一番の突っ込みポイントは、
$\theta$が$90°$までしか定義できない!という点です。
すなわち、
$0<\theta<90°$
の範囲でしかサインやコサインを定義できないという弱点がありました。
ゆえに鋭角は扱いやすいのですが、鈍角となるとちょっと困ってしまうわけです。
そこで、定義を拡張します!!
定義を段々拡張していく、
という作業は数学の研究でけっこうメジャーな手法です。
試してみましょう!
まず、ウルトラマンを呼びます笑

左手が上になるように両手を重ねましょう。
このとき、左手の長さは1だと思ってください。
そして、ウルトラマンポーズで90°の壁を越えます。
左手の指先の軌跡に着目です!!

どうです?
指先の軌跡は円になりました!
腕の長さは1なので、サインとコサインはこう解釈できます
原点を中心とする半径1の円上の点について、
$x$座標(よこの値)をコサイン
$y$座標(たての値)をサイン
とする、と。
図にするとこうです。
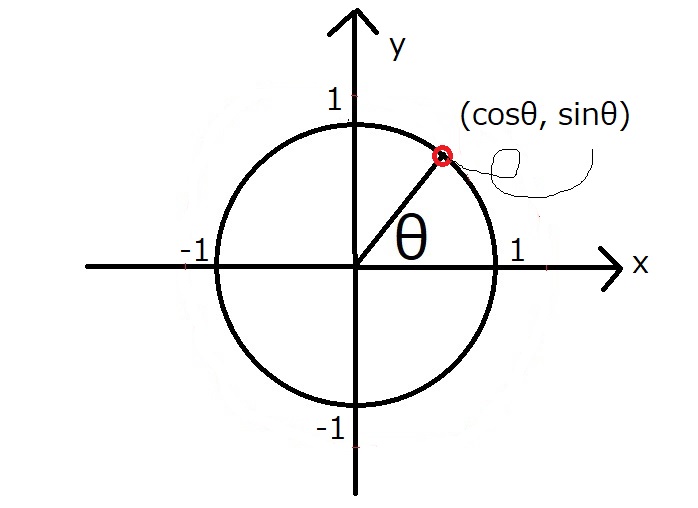
原点を中心とする半径1の円を、
単位円といいます。
つまり、単位円上の点の$x$の値をコサイン、$y$の値をサインと呼ぶよ、
と解釈しなおすと、うまく三角比を一般化できることになります。
式にすると、こうです。
$x^2+y^2=1$
$(x, y)=(\cos \theta, \sin \theta)$
この、一般化された三角比を三角関数といいます。
さて、サインとコサインは分かりました。
じゃ、タンジェントは?
三角比では、タンジェントは傾きと定義されました。
三角関数でも基本的に同じです。
単位円上の点と、原点を結んだ直線の傾きがタンジェントです。
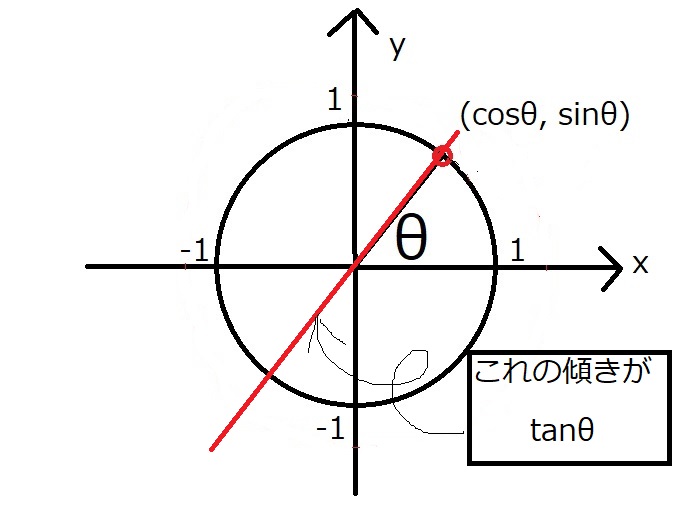
以上、三角関数の定義は終わりです!
三角比の相互関係の公式
① $\sin^2 \theta +\cos^2 \theta=1$
② $\tan \theta =\dfrac{\sin \theta}{\cos \theta}$
③ $\tan^2 \theta +1=\dfrac{1}{\cos^2 \theta}$
です。
さくっと証明しておきましょう。
(①の証明)
$x^2+y^2=1$に$x=\cos \theta, y=\sin \theta$を代入。
$(\cos \theta)^2+(\sin \theta)^2=1$
よって
$\sin^2 \theta +\cos^2 \theta =1$
(証明終了)
(②について)
これはタンジェントの定義より明らかです。
(③の証明)
$\sin^2 \theta+\cos^2\theta=1$
の両辺を$\tan \theta$で割る
$(\dfrac{\sin \theta}{\cos \theta})^2+(\dfrac{\cos \theta}{\cos \theta})^2=(\dfrac{1}{\cos \theta})^2$
よって
$\tan^2 \theta +1=\dfrac{1}{\cos^2 \theta}$
まとめ
・ウルトラマンポーズ流では、直角三角形の
よこの長さをコサイン、たての長さをサインと定義していた。
・しかしウルトラマンポーズ流三角比の定義では、
$0<\theta <90°$までしかサインやコサインを定義できない
・90°の向こう側までウルトラマンポーズすると円ができる
・円上の点のよこの値$(x座標)$をコサイン、
たての値$(y座標)$をサインと定義しなおすと上手くいく
以上です!
また次回の記事でお会いしましょう!

コメント