サイン、コサイン、タンジェント。
三角比とはウルトラマンポーズのことである
三角比の定義
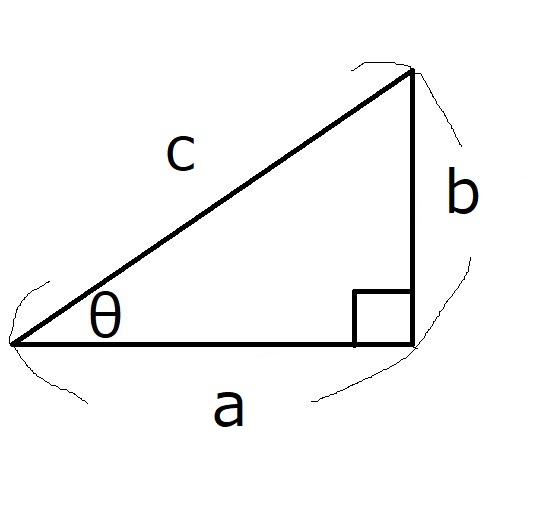
$\sin \theta =\dfrac{b}{c}, \cos \theta =\dfrac{a}{c}, \tan \theta =\dfrac{b}{a}$
と習った人が多いと思います。
定理は証明できますが、定義はひとまず覚えましょう、なんで?とか疑問の余地はありません。
この説明で納得できた人は、ここから先の内容は読まずにそっと記事を閉じてください。
OKですか?
$\sin \theta =\dfrac{b}{c}, \cos \theta =\dfrac{a}{c}, \tan \theta =\dfrac{b}{a}$
定義は覚えるしかない。数学的には確かにそうなんですが、
なんでそう定義すんだよ!
疑問をもつ方もきっといると思います。
そこでこの記事では、三角比の教科書流ではない定義をあたえ、それに基づいて
$\sin \theta =\dfrac{a}{c}, \cos \theta =\dfrac{b}{c}, \tan \theta =\dfrac{a}{b}$
を説明する、というスタンスを取ります。
結局最初は定義を受け入れるところから始まる、という点では同じなのですが、
疑問感をいくらかは払拭できると思います。
高校生の皆さんは、混乱するといけないので学校で習った定義で試験問題は解いてください。
ただし、ウルトラマンとドラえもんが好きな方はこの限りではないので、先へ進みましょう。
では、三角比のマスタノ流定義を導入します。
左手が上になるように両腕を横に重ねてください。
左手の長さを1とします。
そしてウルトラマンのポーズを決めましょう。
はいどうぞ!!

この時の角度を$\theta$とします。
縦の長さが$\sin \theta$で、
横の長さが$\cos \theta$です。
以上!!
はい。
ちょっと説明が乱暴すぎたと思うので、補足です。
三角比を定義するのに必要な材料は3つです
① 基準の長さ1
② 角度$\theta$
③ 直角
さっきの写真をもう一度見てみましょう。
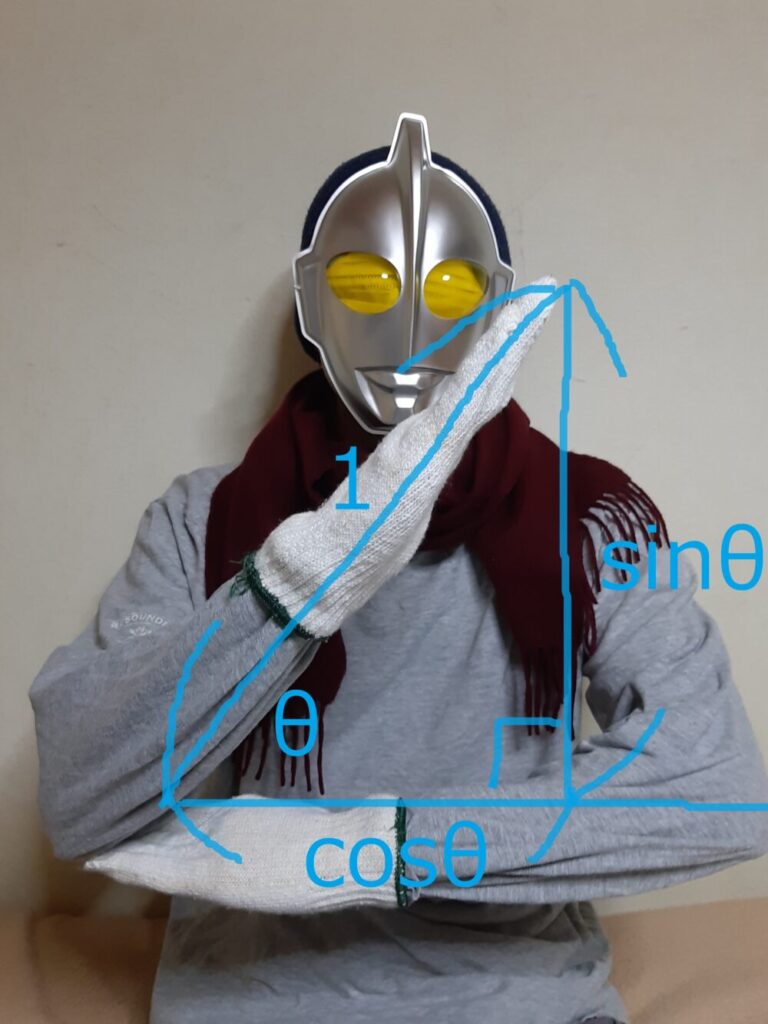
左腕の長さが1です。
左腕の肘と右手の指先がなす角度が$\theta$です。
そして、左手の指先から右腕に向かって垂直に線をひきます。
縦の長さが$\sin \theta$で、
横の長さが$\cos \theta$です。
図を簡略化すると以下のようになります。
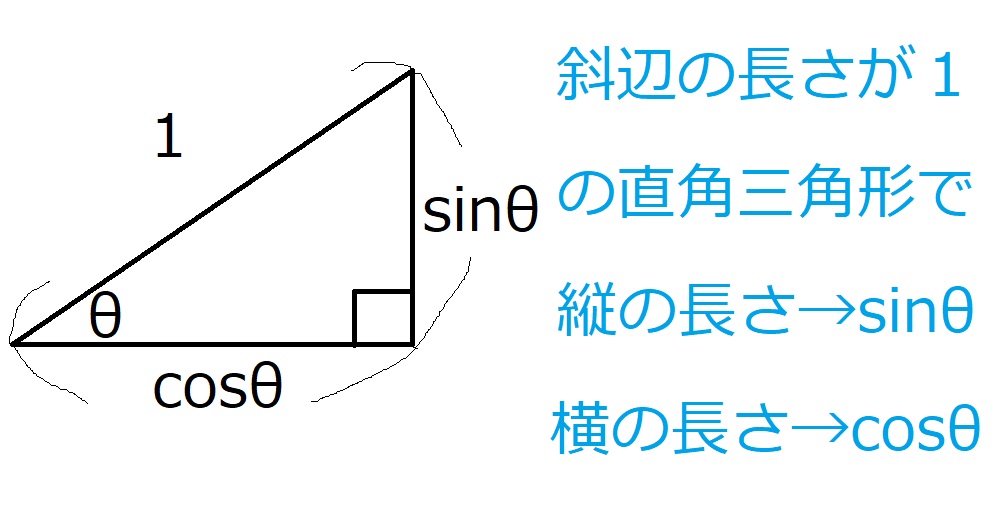
ついでに$\tan \theta$の定義も確認しておきましょう。
タンジェントは、傾きです。
そして、$(傾き)=\dfrac{たて}{よこ}$です。
いま、よこは$\cos \theta, $たては$\sin \theta$なので、
$\tan \theta =\dfrac{\sin \theta}{\cos \theta}$
となります。
このように、三角比は直角三角形を用いて定義されます。
斜辺の長さが1という点がめっちゃ重要なので、覚えておいてください。
また、現時点では三角比を考えているので(三角関数ではない)、
$0°<\theta <90°$です。
$\theta$が90°を超えると直角三角形が作れなくなってしまうので、
三角比を考える間は
$0°<\theta <90°$
と頭の片隅に覚えておいてください。
三角比の定義の仕方はいろんなバリエーションがあるのですが、
僕はこの定義がもっとも素朴で好きです。
なぜこの定義が好きなのか?
それは、三角比の相互関係の公式を一撃で導出できる点にあります。
その前に表記上の注意だけ確認しておきましょう。
三角比では、二乗の表し方が若干独特です。
$(\sin \theta)^2=\sin^2 \theta$と表します。
$\sin \theta^2$とかいてしまうと、
二乗は$\sin$ではなく$\theta$に作用してしまうので要注意です。
二乗以上も同様です。例えば、
$(\sin \theta)^3=\sin^3 \theta$と表すことになります。
さて、ここで、三角比の単元で最も重要といっていい公式を紹介します。
$\sin^2 \theta+\cos^2 \theta=1$
です。これを証明していきたいと思います!
まずは$\sin \theta$と$\cos \theta$の定義の図を見てください。
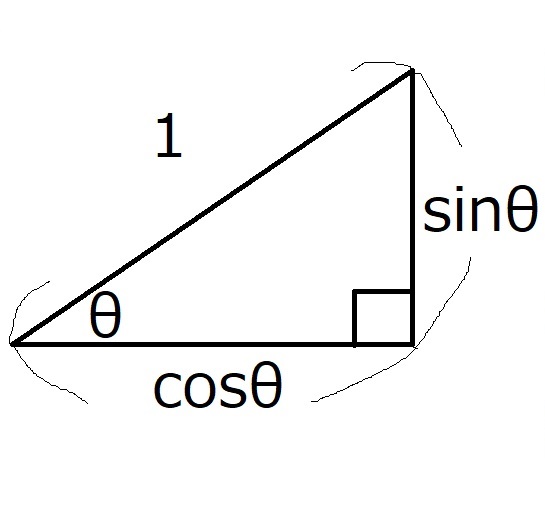
この直角三角形に三平方の定理を使います。
$(\sin \theta)^2+(\cos \theta)^2=1^2$
よって、
$\sin^2 \theta +\cos^2 \theta =1$
はい終わり!
どうです?一撃だったでしょう!?
この疾走感が大好きなので、
三角比の定義はこの直角三角形で理解することをお勧めします。
三角比の相互関係の公式をビッグライトで説明する
さきほどは三角比の相互関係の公式
$\sin^2 \theta +\cos^2 \theta =1$
を三平方の定理で証明しました。
実は、三角比の相互関係の公式はまだ他にもあります。
ここではそれを紹介しようと思うのですが、
その前にドラえもんのビッグライトを思い浮かべてください。
例えば、ビッグライトを僕に向けたとします。
すると僕は巨大化します。
で、5本だった指が6本になるか、というとそんなことはおきません。
何が言いたいかというと、
ビッグライトで変わるのは大きさだけで、形はそのままということです。
ビッグライトやスモールライトで得られる図形は、もとの図形と相似という点が重要です。
では、実際の三角形で今のことを確認していきましょう。
斜辺の長さが2の直角三角形を考えます。
これは、斜辺の長さが1の直角三角形を2倍にビッグライトしたものです。
よって、縦の長さと横の長さも2倍になります。
図にするとこうです。
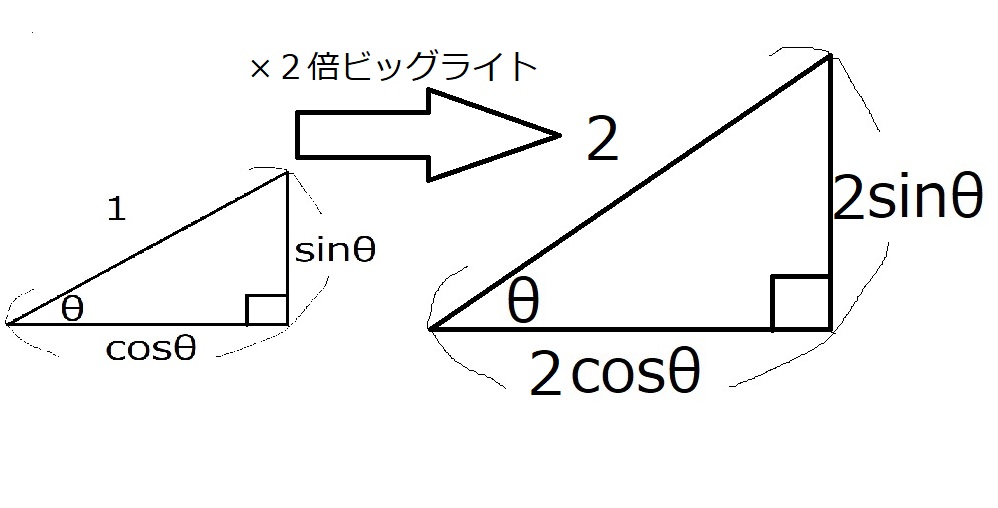
おめでとうございます。
これで三角比を楽しむための道具はそろいました。
具体的な三角形でサインやコサインを求めてみましょう。
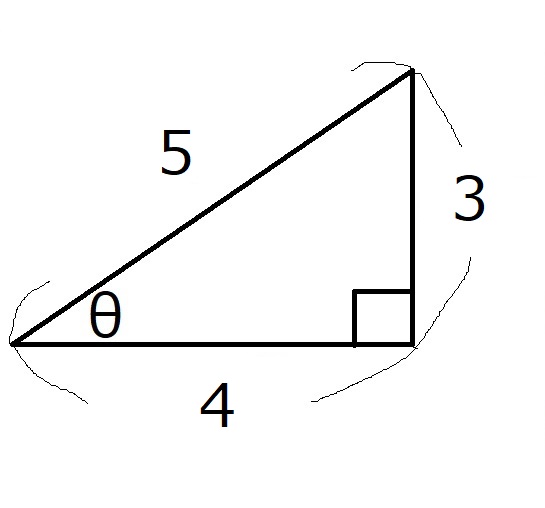
三角比を登場させるのに必要な材料は3つです。
①基準の長さ1 ②角度$\theta$ ③ 直角
今回は、②角度$\theta$と③直角はすでにあります。
でも斜辺の長さが5です!
斜辺の長さを1にしたい!!
→スモールライトだ!!
という思考回路になります。
斜辺の長さを5から1にしたいので、大きさを五分の一にすればよいです。
すると、当然縦の長さを横の長さも五分の一になります。
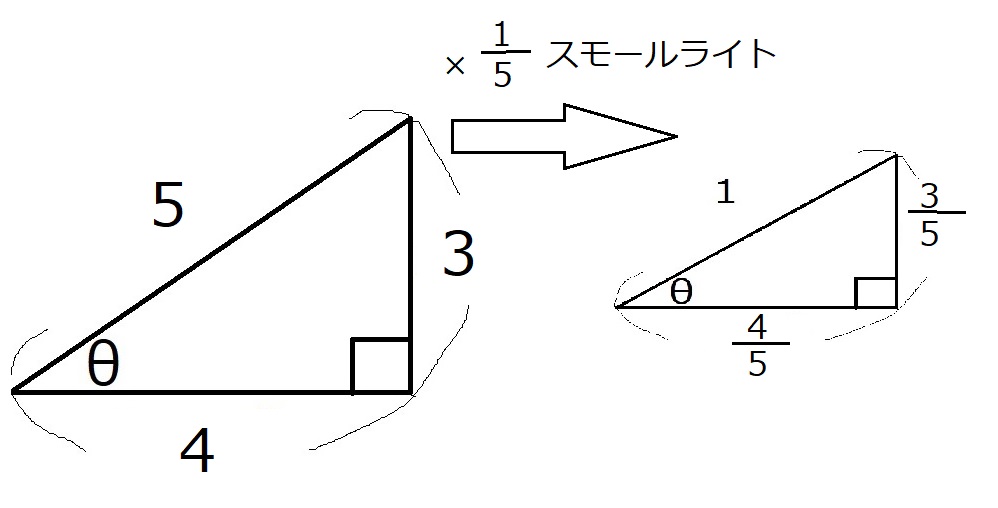
斜辺の長さが1の直角三角形の縦の長さがサイン、横の長さがコサインなので、
$\sin \theta =\dfrac{3}{5}, \cos \theta =\dfrac{4}{5}$
となります。
あとは、今3と4と5でやったことを文字ですれば慣れ親しんだ分数が出てきます。
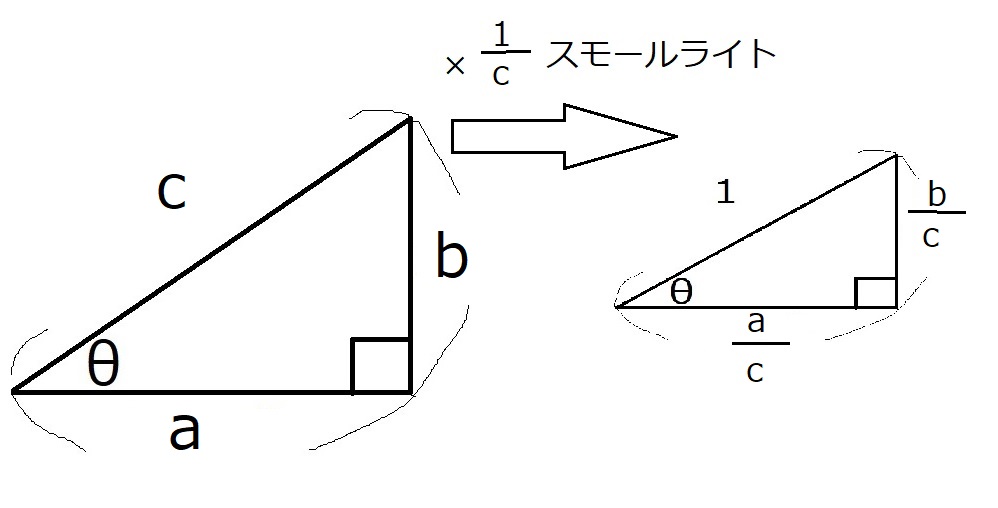
よって$\sin \theta =\dfrac{b}{c}, \cos \theta =\dfrac{a}{c}$です。
$\tan \theta$は傾きなので$\dfrac{たて}{よこ}$となり、$\tan \theta =\dfrac{b}{a}$です。
斜辺が$c$では困るので、長さを1にするために$\dfrac{1}{c}$倍にスモールライトしている、
というのが三角比の本質だったのです。
ビッグライトで説明するって言ったのにスモールライトを使っている!?
ふふ、それはタイトルの文字数を減らしたかったという大人の事情です笑
おまけ
三角比の相互関係の式、最後にもう一つあるので、
一応紹介と証明をしておこうと思います。
ぶっちゃけここは読み飛ばしていただいてOKです。
ではいきましょう
$1+\tan^2 \theta =\dfrac{1}{\cos^2 \theta}$
を証明します。
まずは三角比の定義となる直角三角形を思い浮かべます。
証明のよりどころは、最終的に定義と条件だからです。

さて、この三角形には$\tan \theta$がいません。
そこで、この図に$\tan \theta$を登場させないといけません。
$\tan \theta =\dfrac{\sin \theta}{\cos \theta}$です。
分母に$\cos \theta$がいます。
つまり、$×\dfrac{1}{\cos \theta}$倍にスモールライトです!
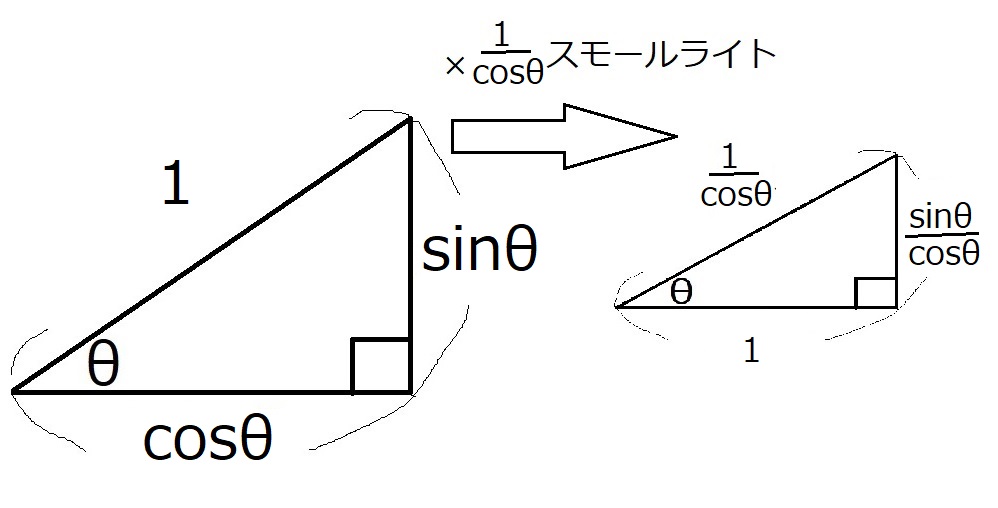
ここで、スモールライトした後の直角三角形について三平方の定理を発動します。
$1^2+(\dfrac{\sin \theta}{\cos \theta})^2=(\dfrac{1}{\cos \theta})^2$
となります。
$\dfrac{\sin \theta}{\cos \theta}=\tan \theta$に留意すると、
$1^2+(\tan \theta)^2=(\dfrac{1}{\cos \theta})^2$
となり、
$1+\tan^2 \theta =\dfrac{1}{\cos^2 \theta}$
が導かれます。
教科書流の定義も一応紹介
教科書ではまず直角三角形が与えられて、

$\sin \theta =\dfrac{b}{c}, \cos \theta =\dfrac{a}{c}, \tan \theta =\dfrac{b}{a}$
が与えられます。この場合もしっかりと
$\sin^2 \theta+\cos^2 \theta=1$は示せるので、確認しておこうと思います。
三平方の定理より、
$a^2+b^2=c^2$です。
全体を$c^2$で割ります。
$(\dfrac{a}{c})^2+(\dfrac{b}{c})^2=1$
三角比の定義より、$\sin \theta =\dfrac{b}{c}, \cos \theta =\dfrac{a}{c}$です。
これを代入すると、
$(\sin \theta)^2+(\cos \theta)^2=1$
となり、
$\sin^2 \theta +\cos^2 \theta =1$
となります。
まとめ
いかがでしたか?
今回は、斜辺の長さが1である直角三角形から出発して
三角比の定義と、相互関係の公式3つ
$\tan \theta dfrac{\sin \theta}{\cos \theta}$
$\sin^2 \theta +\cos^2 \theta =1$
$1+\tan^2 \theta =\dfrac{1}{\cos^2 \theta}$
を紹介&証明しました。
三角比の本質は、斜辺の長さを1にするために拡大・縮小をすること
それをウルトラマンとドラえもんで説明する、というのが今回の趣旨でした。
楽しんでいただけたのなら幸いです。
また次回の記事でお会いしましょう!

コメント