複素数の極形式とは、スイカ割りのことである。
複素数平面スイカ割り
まずはスイカ割りだ!
下の図のように原点に目隠しをした人がいるとします。
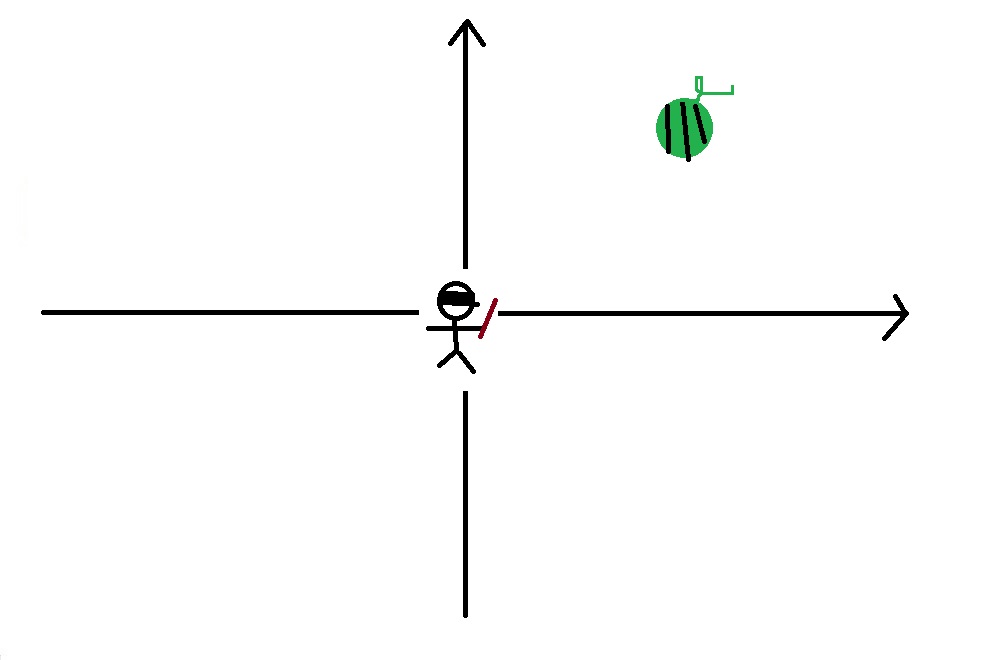
この人をスイカがある位置まで案内できるように指示を出さないといけません。
どうやってこの人をスイカまで案内しましょうか?
斜めにいけー!
とでも指示しましょうか?
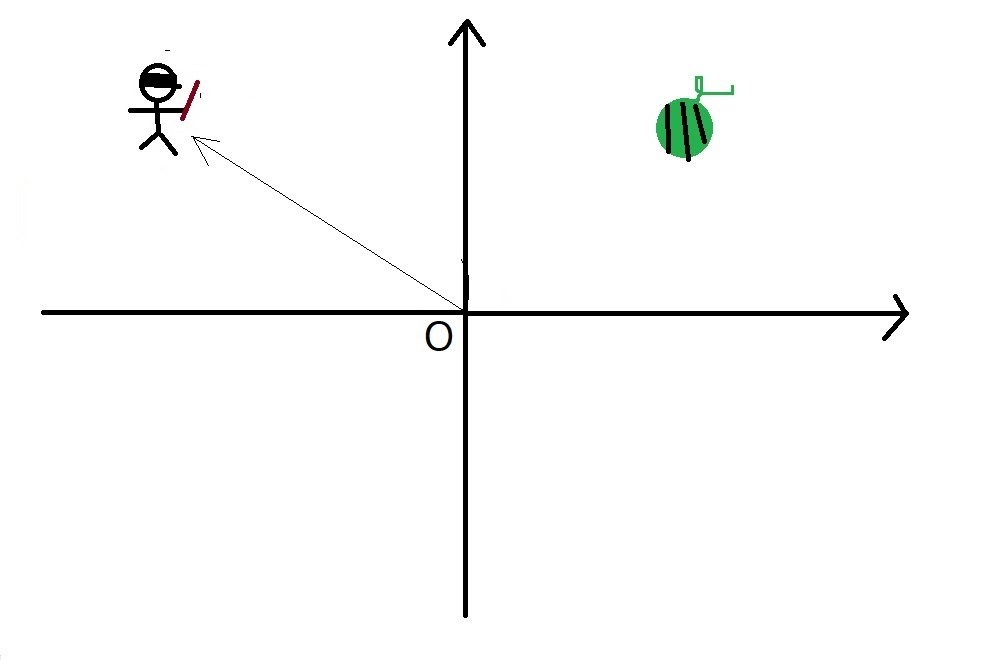
左に行ってしまいました笑
では、
右斜め前にいけー!
と指示してみましょう。
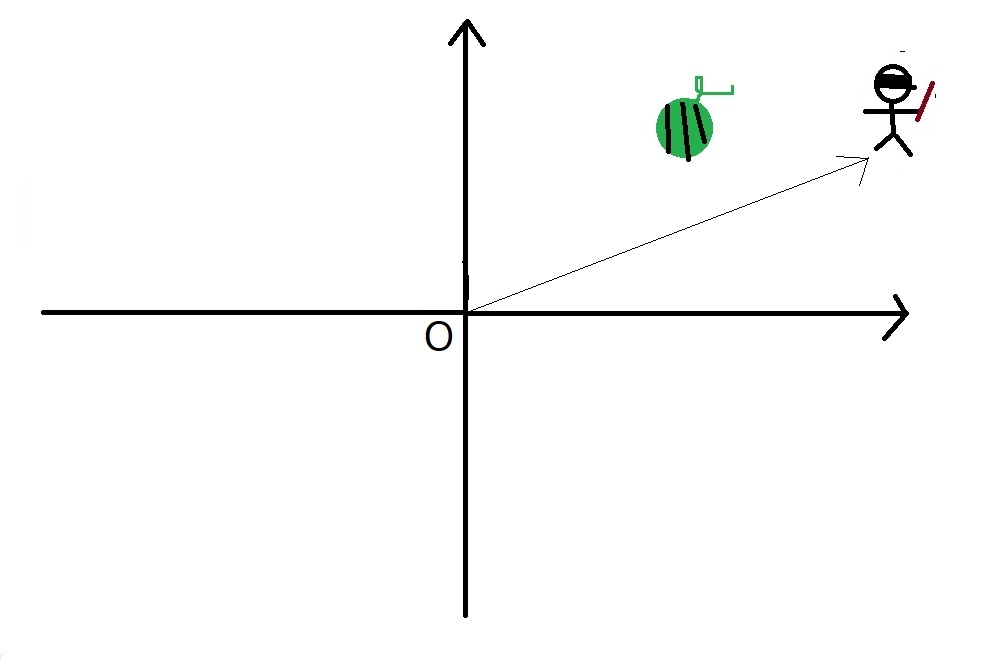
スイカを通り過ぎて行ってしまいました。
右に行って、前にいけー!!
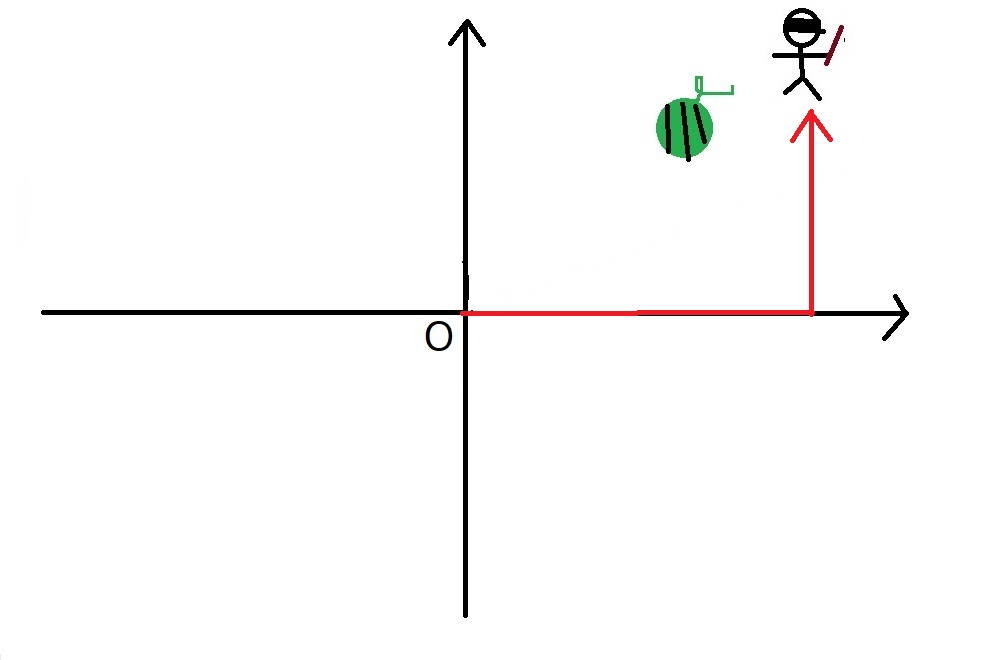
中々思うように進んでくれません笑
なぜか?
指示が数学的ではないからです。
どの方向に、どれだけ進むか、
を明確にしなければなりません。
右に1、左に1進むのだ!
と指示すればスイカにたどり着けます。
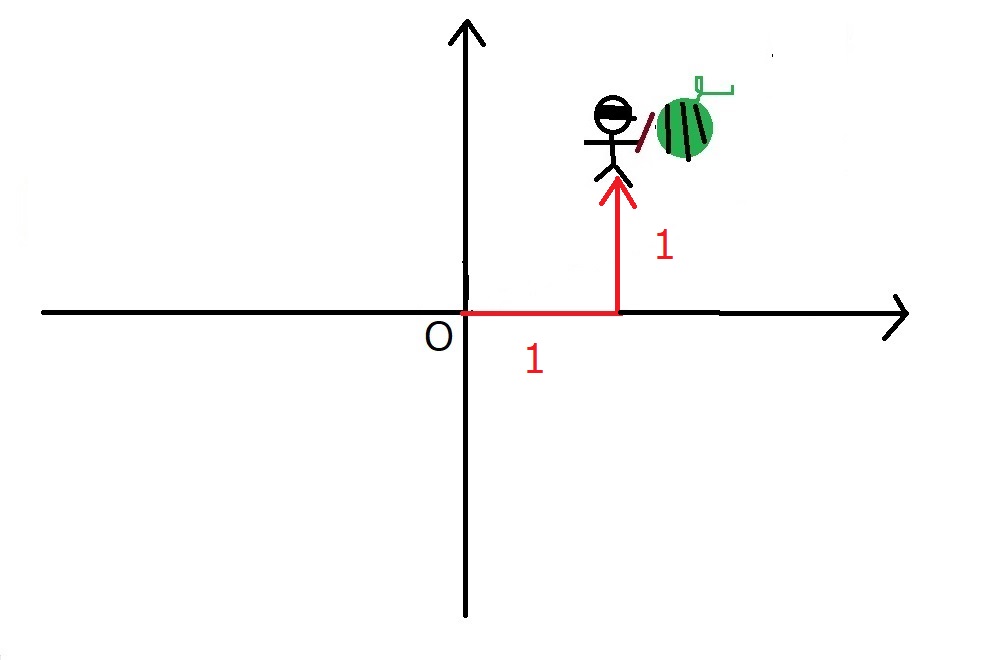
これを複素数で表すと、$1+i$となります。
で、ここからが大切です。
スイカに案内する指示、これだけじゃないですよね。
右斜め45°の方向に、$\sqrt{2}$だけいけー!
という指示目でも目的地に到達できます。
図にすると、こうです。
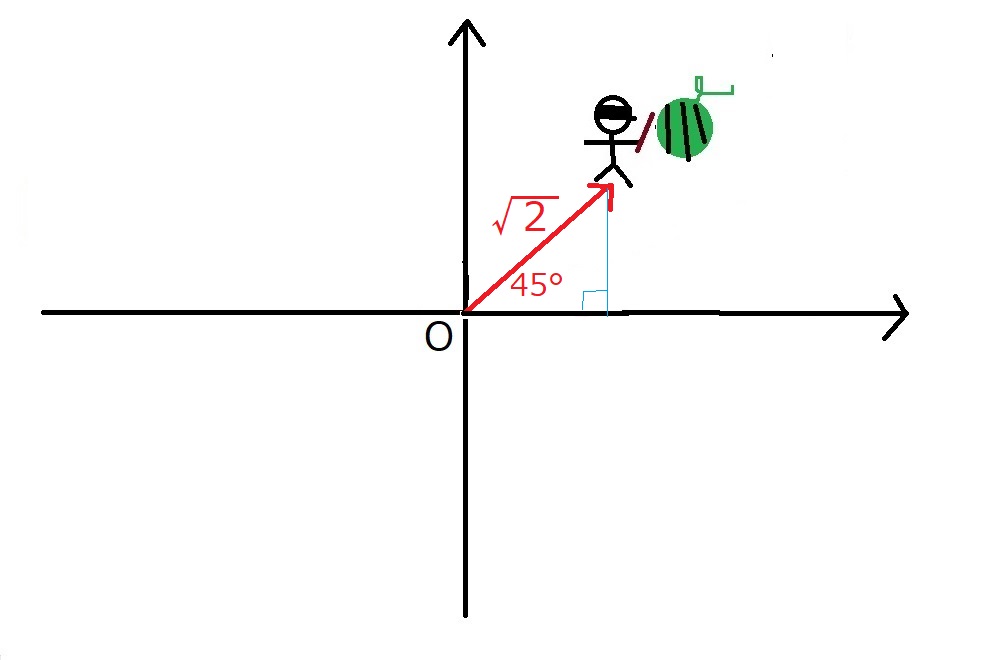
この図を見て、何かを思い出しませんか?
そう、三角比の定義です!
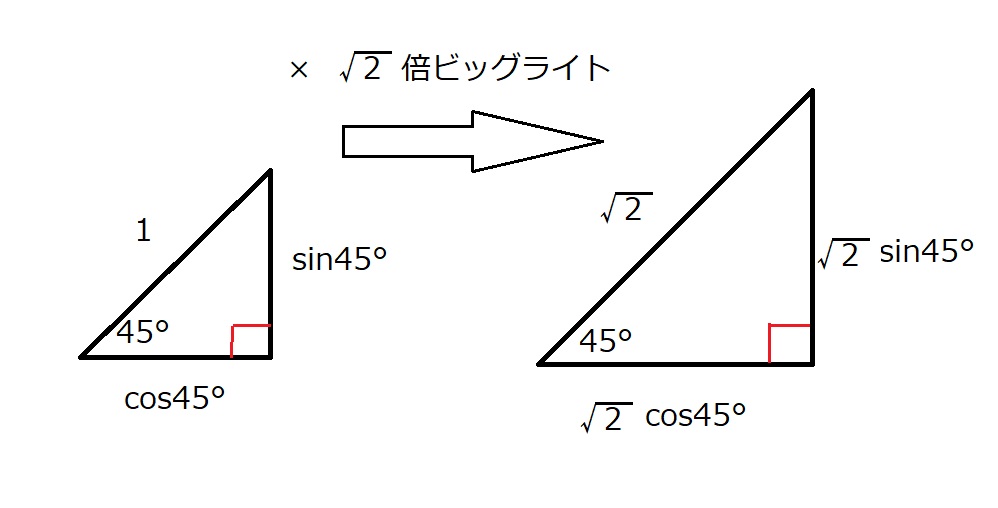
これを使うと、目的の位置は
$\sqrt{2} \sin 45°+i×\sqrt{2}\cos 45°$
となります。
つまり、
$1+i=\sqrt{2}(\sin 45°+i\cos 45°)$
右辺の表し方を極形式と言います。
では、一般に$a+bi$を極形式で表す場合を考えてみましょう。
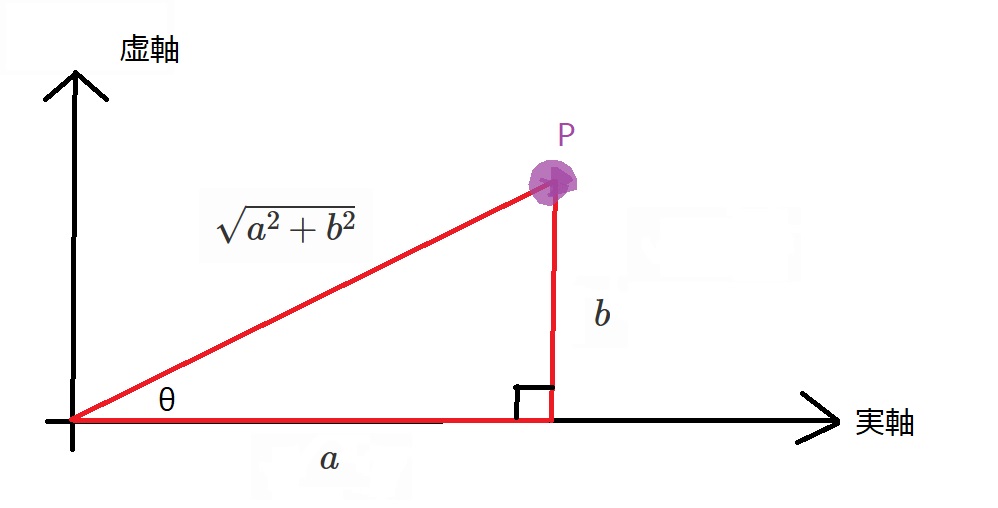
斜辺の長さ(円の半径)は、三平方の定理より$\sqrt{a^2+b^2}$
です。角度を$\theta$とすると、
$a+bi=\sqrt{a^2+b^2}(\cos \theta +\sin \theta)$
となります。
注意しておきたい点として、
$\sqrt{a^2+b^2}$は絶対に正の値ということがあげられます。
$\sqrt{a^2+b^2}$は原点からの距離を表しているからです。
問題演習
複素数を極形式に直す練習をしてみましょう。
手順は簡単
① 図を描く
② 原点からの距離と、角度を求める
③ 円かいて、三角関数の定義に立ち返る
④ 極形式で表す
では実際にやってみましょう!
問題
以下の複素数を極整式で表せ
(1) $\sqrt{3}+i$
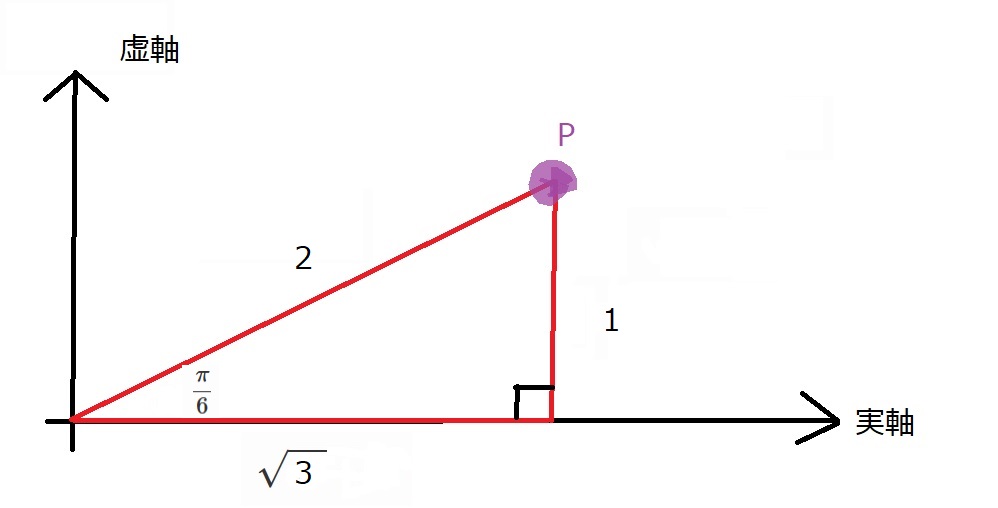
斜辺が2であることと、角度が$\dfrac{\pi}{6}$であることが分かれば十分です。
$\sqrt{3}+i=2(\cos \dfrac{\pi}{6}+i\sin \dfrac{\pi}{6})$
(2) $-1+i$
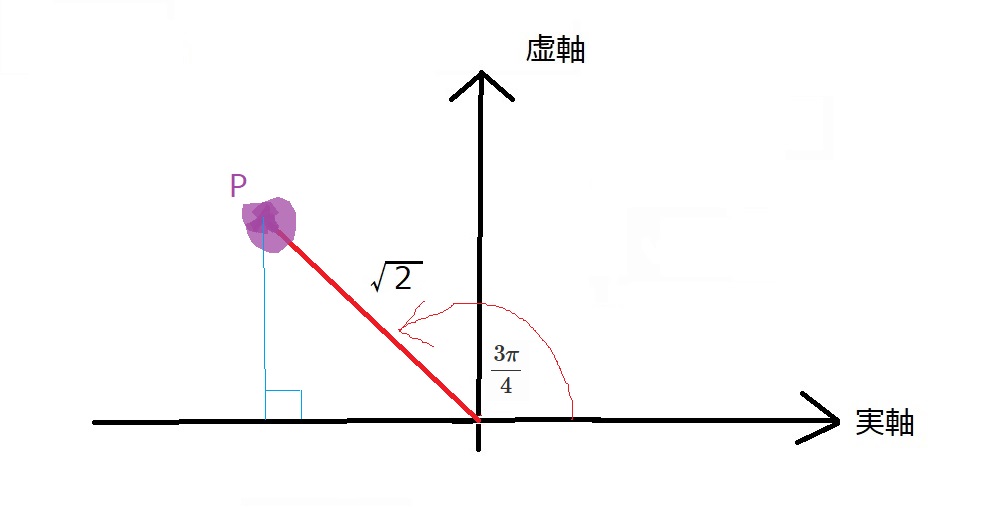
斜めの長さが$\sqrt{2}$です。
$1:1:\sqrt{2}$の直角三角形ができ、
角度は$\dfrac{3\pi}{4}$(180°ー45°=135°を弧度法で表す)です。
よって、
$-1+i=\sqrt{2}(\cos \dfrac{3\pi}{4}+i\sin \dfrac{3\pi}{4})$
となります。
まとめ
いかがでしたか?
・極形式はスイカ割り
・$a+bi=\sqrt{a^2+b^2}(\cos \theta +\sin \theta)$
・斜めの長さと角度が重要
以上3点をマスターしていただければと思います。
ではまた次の記事でお会いしましょう!
コメント