三次方程式が解ける仕組みを、
ラグランジュの分解式(ラグランジュ・リゾルベントともいう)を用いて説明します。
方程式を対称性に着目して分析していく手法です。
この発想の中に、ガロア理論へ至る深遠なひらめきがいくつも隠されているのでご期待ください
2次方程式のおさらい
3次方程式について考えるまえに、まずは2次方程式
$ax^2+bx+c=0$
についておさらいします。
これから解の公式を導くにあたっては、
平方完成を用いるのが最も自然な発想です。
(平方完成を用いた解の公式の導出)
$ax^2+bx+c=0$
$a(x+\dfrac{b}{2a})^2-\dfrac{b^2}{4a}+c=0$
$(x+\dfrac{b}{2a})^2=\dfrac{b^2-4ac}{4a^2}$
$x+\dfrac{b}{2a}=\pm \dfrac{\sqrt{b^2-4ac}}{2a}$
$x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$
ここで、平方完成にたよらずに、
あえて対称式に着目して導出する方法もありました。
(対称式を利用した解の公式の導出)
$ax^2+bx+c=0$
の解を
$x=\alpha, \beta$
とする。
このとき、解と係数の関係より、
$\alpha +\beta=-\dfrac{b}{a}$
$\alpha \beta=\dfrac{c}{a}$
が成立。
ここで、
$\alpha -\beta$
を考える。
これは対称式ではない。
そこで、これを二乗する。
$(\alpha -\beta)^2$
これは対称式であるので、対称式の基本定理より、基本対称式で表すことができる。
実際、
$(\alpha -\beta)^2=(\alpha +\beta)^2 -4\alpha \beta\cdots ①$
ここで、解と係数の関係より
$\alpha +\beta=-\dfrac{b}{a}$
$\alpha \beta=\dfrac{c}{a}$
であったので、これを①に代入すると、
$(\alpha -\beta)^2=\dfrac{b^2}{a^2}-4\dfrac{c}{a}$
$=\dfrac{b^2-4ac}{a^2}$
よって、
$(\alpha -\beta)^2=\dfrac{b^2-4ac}{a^2}$
となり、
$\alpha -\beta =\pm \dfrac{\sqrt{b^2-4ac}}{a}$
である。
したがって、
$\alpha +\beta=-\dfrac{b}{a}$
$\alpha -\beta =\pm \dfrac{\sqrt{b^2-4ac}}{a}$
となり、この連立方程式を解くと
$\alpha, \beta =\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$
となり、解の公式が導出できる。
この解法の一番のポイントは、
「対称式は基本対称式で表すことができる」
→「解と係数の関係より、基本対称式は方程式の係数で表すことができる」
→「解を用いたうまい対称式があれば嬉しい」
→「$\alpha -\beta$が対称式にならないから、二乗して対称性を高める」
→「対称式の基本定理と連立方程式を上手く使って、解を係数(基本対称式で表す)」
→「解の公式完成」
というプロセスです。
特に、
対称式の基本定理を発動するために二乗して対称性を高める
という点が天才的で特筆に値すべき発想なので、覚えておいてください。
2次方程式のおさらいは以上です。
2次方程式の2つの解法について興味をもった方は、以下の記事をご覧ください
平方完成を用いた解法

対称式を用いた解法

3次方程式とラグランジュの分解式
ここからラグランジュの分解公式を用いて3次方程式を考察していきますが、
その前に、3次方程式の解の公式を普通に導出するやり方を知っておいた方が
はるかに理解が深くなります。
平方完成を進化させた立方完成というテクニックと、
あえて文字を増やして上手く2次方程式の解と係数の関係に帰着させるという
発想が天才的です。
解の公式を得る過程の概略だけ述べておくと、
①$ax^3+bx^2+cx+d=0$の全体を$a$で割って最高次の係数を$1$にする
②立方完成を用いて置き換えをし、
$y^3+py+q=0$という形に式を簡略化する
③$y=s+t$という置き換えをする
④式を上手く整理し、2次方程式の解と係数の関係を発動
⑤ゲットした2次方程式を解く(3次方程式を2次方程式に帰着させる)
⑥$S^3=A$ $T^3=B$ という形の式の三乗根を取る
⑦$ST$が実数という条件を使って絞り込みをする
⑧解の公式、完成
結構な長編ストーリーです。
細かいテクニックは後回しでよいので、
3次方程式を2次方程式に帰着させる
という点だけ覚えておいてください。
より詳しく丁寧な解説は、以下の記事をご覧ください。
カルダノの公式

ラグランジュの分解式を用いた3次方程式の解ける仕組みの考察では、
対称性という発想がキーワードとなります。
2次方程式の場合は、
$(\alpha -\beta)^2$
という式を発見できた点が成功の秘訣でした。
2次方程式の解の個数は2個です。
2個の解の入れ替え方法は、2!=2 通りです。
解を
$x=\alpha, \beta$
とすると、具体的な入れ替え方は
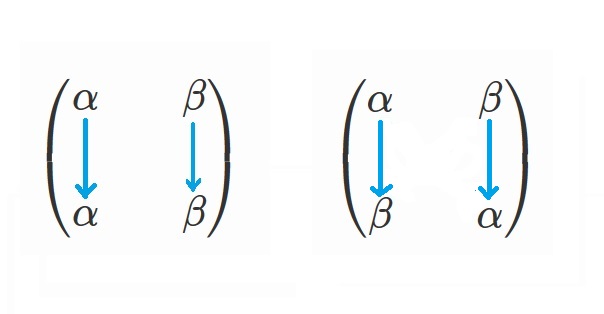
の二つです。
$(\alpha -\beta)^2$
はこの2つの入れ替えで不変なので、対称式であり、
対称式の基本定理から基本対称式で表すことができたわけです。
これを3次方程式の場合に応用していきます。
まず、最初のハードルとなるのは、
3次方程式における
$(\alpha -\beta)^2$
のような対称式をどうやって見つけてくるか、という点です。
ここで、ラグランジュさんの天才的なひらめきが輝きます。
まずラグランジュさんは
$\alpha -\beta$
に注目しました
$\alpha -\beta=1×\alpha +(-1)×\beta$
という眺め方をしたのです。
そして、$1$と$-1$は、
$x^2-1=0$
の解じゃね!?ということに気が付きました。
これです。これがラグランジュさんが天才たる所以です。
これを3次方程式に応用しましょう。
三次方程式
$ax^3+b^2+cx+d=0$
の3つの解を
$x=\alpha, \beta, \gamma$
とします。
そして、
$x^3-1=0$
の解を考えましょう。
$x^3-1=0$
の解は、
$x=1, \omega, \omega^2$
です。これらを用いて、
$\alpha +\omega \beta +\omega^2 \gamma$
という式を考えます。
これが3次方程式の
ラグランジュの分解式(ラグランジュ・リゾルベント)
です。
ここから対称性に着目しつつ考察を進めていきましょう!
まず、3次方程式の3つの解の並び替えの方法は
3!=6 通りです。
具体的には、
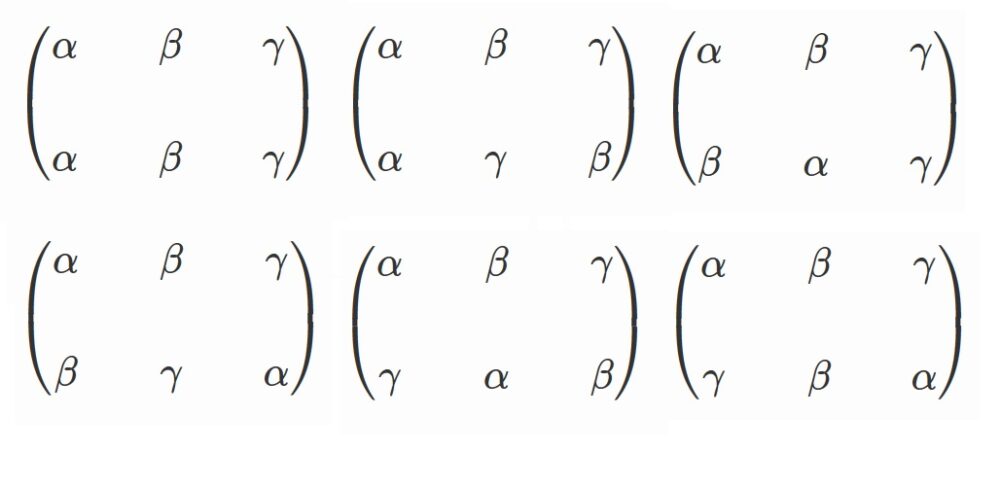
の6つです。
これらの並び替えを
$\alpha +\omega \beta +\omega^2 \gamma$
に作用させると、以下のように6通りの式ができます。
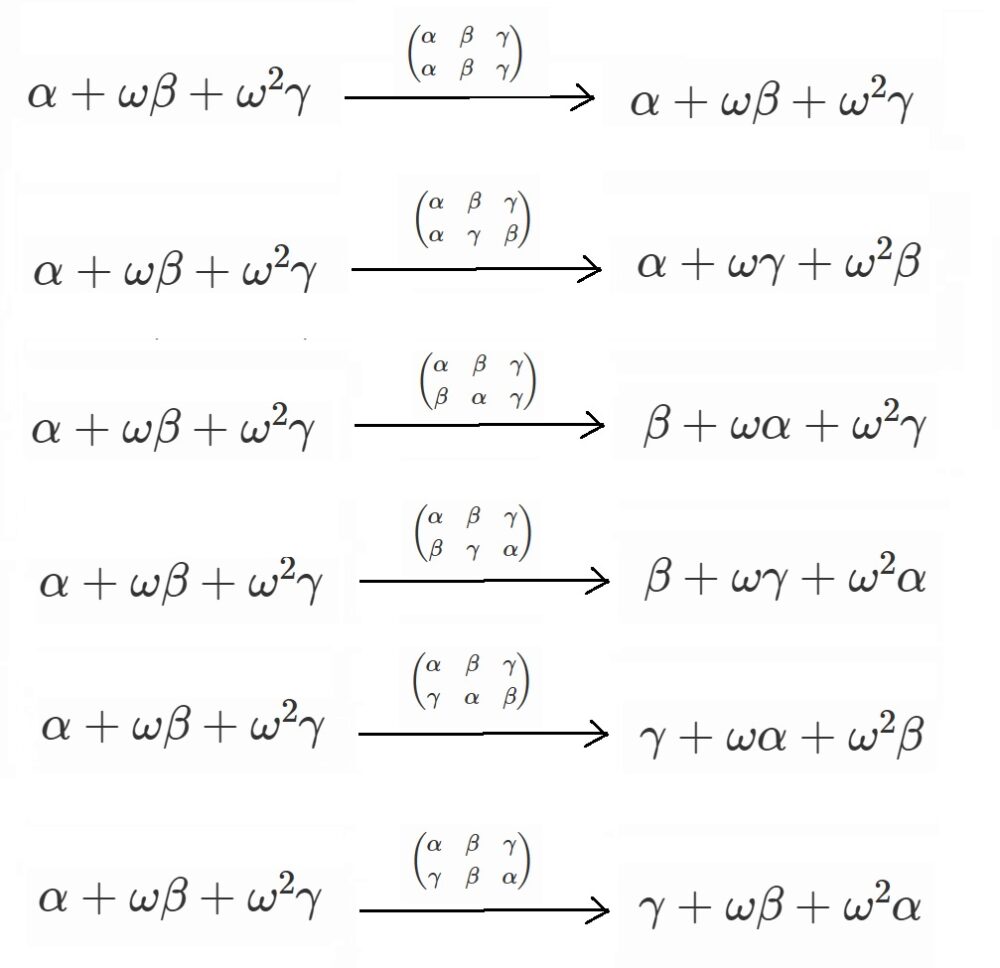
要するに、
$\alpha +\omega \beta +\omega^2 \gamma$
は並び替えで不変ではなく、対称性はめっちゃ低い状態です。
そこで、2次方程式の時に
$\alpha -\beta$
を二乗したように、
$\alpha +\omega \beta +\omega^2 \gamma$
を3乗してみましょう!
$(\alpha +\omega \beta +\omega^2 \gamma)^3$
に6通りの並び替えを作用させてみます。
例えば、
$(\alpha +\omega \beta +\omega^2 \gamma)^3$に
\begin{pmatrix}
\alpha &\beta & \gamma \\
\beta & \gamma & \alpha
\end{pmatrix}
を作用させてみましょう。
すると、
$(\beta +\omega \gamma +\omega^2 \alpha)^3$
が出現します。
ここで、
$\beta +\omega \gamma +\omega^2 \alpha=\omega^2(\alpha +\omega \beta +\omega^2 \gamma)$
に注意すると、
$(\beta +\omega \gamma +\omega^2 \alpha)^3=\lbrace \omega^2(\alpha +\omega \beta +\omega^2 \gamma) \rbrace^3$
$=\omega^6(\alpha +\omega \beta +\omega^2 \gamma)^3$
$=(\alpha +\omega \beta +\omega^2 \gamma)^3$
です!
つまり、
$(\alpha +\omega \beta +\omega^2 \gamma)^3$は
\begin{pmatrix}
\alpha &\beta & \gamma \\
\beta & \gamma & \alpha
\end{pmatrix}
という並び替えでは不変だったわけです。
もし、
$(\alpha +\omega \beta +\omega^2 \gamma)^3$
が3!=6 通りのすべての並び替えで不変なら、これは対称式であるということになります
試してみましょう。

おしい!
$(\alpha +\omega \beta +\omega^2 \gamma)^3$
はまだ6つの並び替えで不変ではないので、対称式ではありません
しかし、です。
$\alpha +\omega \beta +\omega^2 \gamma$
のときとちがって、
$(\alpha +\omega \beta +\omega^2 \gamma)^3$
は
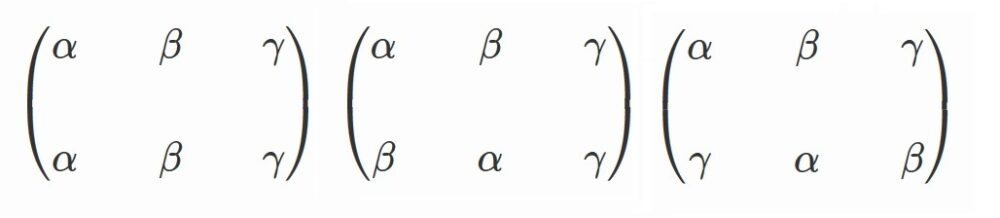
の3つの並び替えでは不変です。
完全ではないものの、
先ほどよりも大幅に対称性が高まっています。
加えて、
$\alpha +\omega \beta +\omega^2 \gamma$
は6つの並び替えを作用させると6通りの式が出てきていましたが、
$(\alpha +\omega \beta +\omega^2 \gamma)^3$
は2通りしか式が出てきませんでした。
式が減っています!
そこで、
$(\alpha +\omega \beta +\omega^2 \gamma)^3=S^3$
$(\alpha +\omega \gamma +\omega^2 \beta)^3=T^3$
と文字で置くことにします。
$S^3$ と $T^3$
の2つの文字の対称式を見つければよいことになります。
ここで式が2種類しか出てこないから、
カルダノの公式で
3次方程式を2次方程式に帰着させることができたのです。
ですので、対称性についても、2次方程式の議論を流用しましょう
$(S^3-T^3)^2$
です!
具体的に書き下すと、
$(S^3-T^3)^2=\lbrace (\alpha +\omega \beta +\omega^2 \gamma)^3-(\alpha +\omega \gamma +\omega^2 \beta)^3 \rbrace^2$
です。
試してみると分かりますが、これは6つの並び替えで不変です。
したがって、対称式の基本定理から、
$(S^3-T^3)^2$
は$\alpha, \beta, \gamma$
の基本対称式
$\alpha +\beta +\gamma$
$\alpha \beta +\beta \gamma +\gamma \alpha$
$\alpha \beta \gamma$
で表されることになります
そして、3次方程式の解と係数の関係より、
$\alpha +\beta +\gamma=-\dfrac{b}{a}$
$\alpha \beta +\beta \gamma +\gamma \alpha=\dfrac{c}{a}$
$\alpha \beta \gamma=-\dfrac{d}{a}$
でしたので、
$(S^3-T^3)^2$
は結局、3次方程式$ax^3+bx^2+cx+d=0$
の係数$a, b, c, d$で表されることになります※(補足参照)
そこで、
$(S^3-T^3)^2=D$ $(Dはa, b, c, d で表されている)$
と置くことにします。
すると、
$S^3-T^3=\pm \sqrt{D}$
です。
また、
$S^3+T^3= (\alpha +\omega \beta +\omega^2 \gamma)^3+(\alpha +\omega \gamma +\omega^2 \beta)^3 $
もまた$\alpha, \beta, \gamma$の対称式なので、
対称式の基本定理から基本対称式で表すことができ、
解と係数の関係から、結局は3次方程式の係数$a, b, c, d$で表されます。
そこで、
$S^3+T^3=E$ $(Eはa, b, c, dで表されている)$
と置くことにします。
$S^3+T^3=E$
$S^3-T^3=\pm \sqrt{D}$
を解くと、
$S^3, T^3$
が$a, b, c, d$と平方根で表されることになります。
$S^3=F, T^3=G$
と置き、三乗根をとると
$S$ と $T$ が$a, b, c, d$と平方根と三乗根で表されることにまります。
そこで、
$S=s, T=t$ $s, tはa, b, c, dと平方根と三乗根で表されている$
と置くことにしましょう。
すると、解と係数の関係の1番目の式と合わせて、
$\alpha +\beta +\gamma =-\dfrac{b}{a}\cdots ㋐$
$\alpha +\omega \beta +\omega^2 \gamma =s\cdots ㋑$
$\alpha +\omega^2 \beta +\omega \gamma=t\cdots ㋒$
という3つの連立方程式が出現します。
ここで、$\omega$
が円分多項式
$\Phi_3(x)=x^2+x+1$
の解であったことを思い出しておきましょう。
つまり、
$\omega^2+\omega+1=0$
です。
これを踏まえて、㋐+㋑+㋒をします。
$3\alpha +(1+\omega +\omega^2)\beta +(1+\omega^2+\omega)\gamma=-\dfrac{b}{a}+s+t$
となり、$\omega^2+\omega +1=0$
から、
$3\alpha =-\dfrac{b}{a}+s+t$
$\alpha =\dfrac{1}{3} (\dfrac{-b}{a}+s+t)$
となり、$\alpha$を三次方程式の係数$a, b, c, d$と平方根と三乗根で表すことができました。
$\beta$については、
$㋐+㋑×\omega^2+㋒×\omega$より、
$\beta =\dfrac{1}{3}(\dfrac{-b}{a}+\omega^2s+\omega t)$
と求まり、$\gamma$は
$㋐+㋑×\omega + ㋒×\omega^2$
で
$\gamma =\dfrac{1}{3}(\dfrac{-b}{a}+\omega s+\omega^2 t)$
と求まります。
結論、
$\alpha =\dfrac{1}{3} (\dfrac{-b}{a}+s+t)$
$\beta =\dfrac{1}{3}(\dfrac{-b}{a}+\omega^2s+\omega t)$
$\gamma =\dfrac{1}{3}(\dfrac{-b}{a}+\omega s+\omega^2 t)$
から、3つの解$\alpha, \beta, \gamma$は
三次方程式の係数$a, b, c , d$と平方根と三乗根で表されることが確認できました。
さて。
次の見出しでは、ここまでの流れを体(たい)という概念を使ってまとめなおしてみようと思います。
※(補足)
$(S^3-T^3)^2=\lbrace (\alpha +\omega \beta +\omega^2 \gamma)^3-(\alpha +\omega \gamma +\omega \beta)^3 \rbrace^2$
の右辺を超がんばって整理すると、
$-27(\alpha -\beta)^2(\beta-\gamma)^2(\gamma -\alpha)^2$
となり、確かにこれは対称式です。
実は、これは2次方程式で言う判別式$D$と同じ役割を果たす式で、
重解を持つかどうかの判別に使うことができます。
判別式の一般化についてもどこか別の記事で紹介しようと思いますので、
ご期待ください。
体(たい)で捉えなおす
先ほどまでの議論を体(たい)という概念を使って捉えます。
体(たい)とは、簡単に言えば四則演算で閉じた集合です。
詳しくはこちらの記事を参照ください

まずは2次方程式から考えていきましょう。
2次方程式の解の公式は
$x=〇+△\sqrt{b^2-4ac}$
という形をしているので、
$\mathbb{Q}(\sqrt{b^2-4ac})=\lbrace s+t\sqrt{b^2-4ac}|s, t \in \mathbb{Q} \rbrace$
を考えると、
$x \in \mathbb{Q}(\sqrt{b^2-4ac})$
となり、
$\mathbb{Q} \subset \mathbb{Q}(\sqrt{b^2-4ac})$
です。
したがって、2次方程式を解くという作業は、
係数の世界を$\mathbb{Q}$から$\mathbb{Q}(\sqrt{b^2-4ac})$に広げる作業と読み替えることができます。
次に3次方程式について。
3次方程式では、
$x^3=0$の解$1$と$\omega$と$\omega^2$
を用いて
$\alpha +\omega \beta +\omega^2 \gamma$
という式を考えました。
これを3次方程式のラグランジュ・リゾルベントです。
ラグランジュ・リゾルベントを3乗すると
$(\alpha +\omega \beta +\omega^2 \gamma)^3$
が得られます。
これは対称式ではないものの、3!通りの解の入れ替えのうち、
いくつかで不変で、対称性が大幅に上がっていました。
そのうえ、入れ替えでは2通りの式しか出現しません。
$S^3=(\alpha +\omega \beta +\omega^2\gamma)^3$
$T^3=(\alpha +\omega^2 \beta +\omega \gamma)^3$
と置くと、
$(S^3-T^3)^2$
は対称式となり、2次方程式のやり方が適応できます。
そして、$S^3$と$T^3$の三乗根をとって解を求めました。
これをまとめると
①まず有理数$\mathbb{Q}$と$\omega$からラグランジュ・リゾルベントを作る
②$S^3$と$T^3$の2次方程式を解く
③$S^3$と$T^3$の三乗根を取って解をゲットする
という流れになります。
これを体で表すと、
$\mathbb{Q}(\omega) \subset \mathbb{Q}(\omega, \sqrt{(S^3-T^3)^2}) \subset \mathbb{Q}(\omega, \sqrt{(S^3-T^3)^2}, S, T)$
となります。
この「係数の体の世界を広げる作業」と、
「並べ替えを使って対称性を高めていく作業」の
2つの間に隠された神秘的な関係性を解き明かしたのがガロアであり、ガロア理論です。
まとめ
いかがでしたか?
・方程式を解くにあたって、解の並べ替えについて対称性を高める作業が重要
・その際、ラグランジュの分解式(ラグランジュ・リゾルベント)が便利だった
以上2点を抑えていただければと思います。
今後の記事で4次方程式の場合のラグランジュ・リゾルベントの話と、
あと$x^n-1=0$のラグランジュリゾルベントの話をすると、
方程式の解法の観察としては十分なので、
それらの解法の共通点・規則性を観察し、ガロア理論へつなげていこうと思います。
ご期待ください。
参考
画像素材提供(アイキャッチ):Peace,love,happinessによるPixabayからの画像
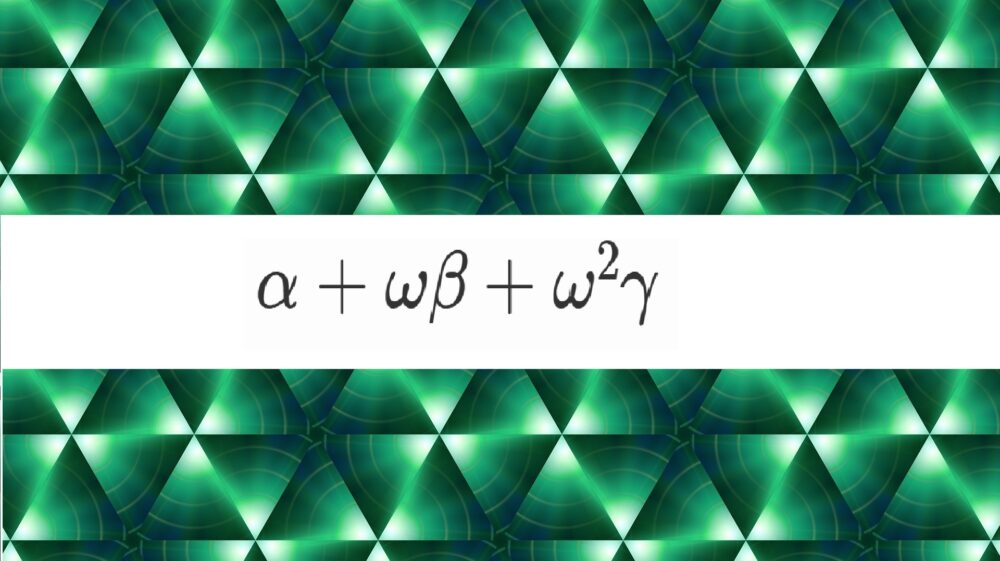
コメント