平方完成で求める２次方程式の解の公式

まずはシンプルな形から

２次方程式史上最もシンプルなものは、おそらく

$x^2=4$

型の２次方程式だと思います。

$x^2=4$より、$x=2, -2$です。

はい完了！簡単です。

$x^2=a$型の２次方程式をパターン①とします。

パターン①の２次方程式は、$x^2=a$から直ちに$x=\pm \sqrt{a}$と解を求めることができます。

では、一般の２次方程式$ax^2+bx+c=0$はどうしましょうか？

これをパターン②としましょう。

２次方程式の解の公式を導出してみよう！

基本となる考えは、パターン②をどうにかパターン①にしたい、という発想です。

パターン①とパターン②を見比べて、何が違うか、どこが難しい原因か見極めます。

まず、シンプルな違いとして、パターン①は$x^2$の係数が１ですが、

パターン②では$x^2$の係数が$a$です。

そこで、パターン②の$x^2$の係数を１にしたい、という発想が生まれます。

パターン②の全体を$a$で割りましょう。

$x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0$

さて、少しだけパターン①に近づきましたが、まだまだ違いは大きいです。

次に特徴的な違いとして、パターン①には$x$の項がないのに対し、パターン②には$x$の項が存在します。

これが難しい原因です。

そこで、パターン②を変形して$x$の項がない形、すなわち$〇^2=△$の形にしよう！という発想になります。

どうするか？

平方完成です！！

平方完成のざっくりしたおさらい

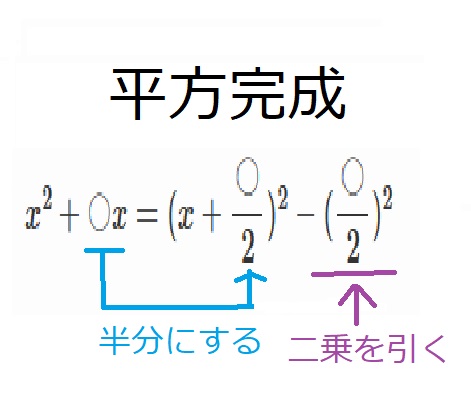
$x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0$を平方完成します。

$(x+\dfrac{b}{2a})^2-(\dfrac{b}{2a})^2+\dfrac{c}{a}=0$

$(x+\dfrac{b}{2a})^2-\dfrac{b^2}{4a^2}+\dfrac{c}{a}=0$

$(x+\dfrac{b}{2a})^2=\dfrac{b^2-4ac}{4a^2}$

これでパターン①の形になりました！あとはルートをとります。

$x+\dfrac{b}{2a}=\pm \dfrac{\sqrt{b^2-4ac}}{2a}$

よって$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

となります。

いわゆる２次方程式の解の公式ですね！

まとめ

いかがでしたか？

平方完成を使って$〇^2=△$の形を作る！

という点だけ覚えていただければと思います。

余談ですが、僕は学生時代解に解の公式が中々覚えられず、毎回平方完成をつかって導出していました。

定期テスト前は導出しすぎて逆に覚えていたのですが、高３になると主に微積に時間を割くので、

久しぶりに２次方程式を解かなければならなくなった時、公式を思い出せずに模試の会場で焦った記憶があります笑

でも大丈夫。

平方完成を使う、ということだけ覚えておけば、忘れてもまた解の公式に出会えます。