$x^n-1$の分解
整数係数多項式
あと$\mathbb{Q}$上の規約性
これらが円分多項式の著しい性質。
今回は、$x^n-1$の分解と、整数係数多項式であることを実験的に学び、
証明でフィナーレを飾りましょう!
定義のおさらいから
円分多項式の定義を確認しましょう。
結構えぐい数式が出てきますが、あとで具体例を確認しますので、ご容赦を。
新しい数学を学ぶときは、
えぐい数式発見→意味不明で焦る→具体例を確かめる→納得して落ち着く
の繰り返しで前に進んでいくものです。
円分多項式の定義は、
(定義)
$\zeta_n=\cos \dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とする。
このとき、
$\Pi_{GCD(n, k)=1, 1≦k≦n}(x-\zeta_n^k)$
を円分多項式といい、$\Phi_n(x)$で表す
というものでした。
記号を確認していきましょう。
まず$\Pi$。
これは和の記号シグマの掛け算バージョンです。
次に$GCD(n, k)=1$
これは、$n$と$k$の最大公約数が1(互いに素)だよ、という意味です。
まずは$\Phi_4(x)$を考えてみましょう。
$GCD(4, k)=1, 1≦k≦4$を処理します。
1,2,3,4
のうち、4と互いに素なのは
1と3です。
よって$k=1, 3$となります。
次に$\Pi$です。
これは掛け算なので、
$(x-\zeta_4)$と$(x-\zeta_4^3)$を掛け算することになります。
$\Phi_4(x)=(x-\zeta_4)(x-\zeta_4^3)$
です。
ここで、$\zeta_4$とかなんか難しい記号で書いてますが、
要するにこれは$i$のことです。
それを確かめておきましょう。
$\zeta_4=\cos \dfrac{2\pi}{4}+i\sin \dfrac{2\pi}{4}$
$=\cos \dfrac{\pi}{2}+i\sin \dfrac{\pi}{2}$
ここで、$\cos \dfrac{\pi}{2}=0, \sin \dfrac{\pi}{2}=1$に注意すると、
$\zeta_4=i$です。
つまり、
$\Phi_4(x)=(x-i)(x-i^3)=x^2-i^3x-ix+i^4=x^2+1$
となります。
次は少し複雑な$\Phi_{12}$を考えてみましょう。
まず
$GCD(12, k)=1, 1≦k≦12$
を処理します。
1,2,3,4,5,6,7,8,9,10,11,12
のうち、12と互いに素なものは、
1,5,7,11です。
よって$k=1, 5, 7, 11$となります。
あとは$\Pi$ですね。これは掛け算です。
$(x-\zeta_{12})$や$(x-\zeta_{12}^5)$などを掛け算すればよいのです。
したがって、
$\Phi_{12}(x)=(x-\zeta_{12})(x-\zeta_{12}^5)(x-\zeta_{12}^7)(x-\zeta_{12}^{11})$
です。
$\zeta_{12}$は$\zeta_4$の時のようにシンプルに表せる数ではないので計算は省略しますが、
頑張って右辺を展開して整理すると
$\Phi_{12}(x)=x^4-x^2+1$
というなんともシンプルな式が出てきます。
円分多項式ってなんであんなヤバい定義なの?
という点が気になる方は以下の記事をご覧ください。
円分多項式を発見する過程を追体験してみませんか?

円分多項式の性質① $x^n-1$の因数分解
円分多項式の面白いところは、
何といっても$x^n-1$の因数分解です。
例えば$x^{12}-1$を考えましょう。
これは、円分多項式を用いて次のように因数分解されます。
$x^{12}-1=\Phi_1(x)\Phi_2(x)\Phi_3(x)\Phi_4(x)\Phi_6(x)\Phi_{12}(x)$
見事に12の約数の円分多項式が並んでいます。
これが一般に$x^n-1$の場合も成り立ちます
ヤバくないですか?
これを証明します。
(定理)
$x^n-1=\Pi_{d|n}\Phi_d(x)$
が成り立つ
ここで、
$d|n$
という記号が見慣れないと思うので、補足します。
これは、$d$は$n$の約数ですよ、という意味です。
~脳内会議~
いきなり証明せよ、と言われても何から手を付ければいいのやらさっぱりです。
このような時は、具体例の観察が非常に重要となります。
とりあえず、小さめの数の$n=6$の場合で検討してみましょう。
$x^6-1=(x-\zeta_6)(x-\zeta_6^2)(x-\zeta_6^3)(x-\zeta_6^4)(x-\zeta_6^5)(x-\zeta_6^6)$
です。
これを、$x^6-1=\Phi_1(x)\Phi_2(x)\Phi_3(x)\Phi_6(x)$
から逆算的に並び替えてみましょう。
$x^6-1=0$の解は
$x=\zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5, \zeta_6^6(=1)$
で、複素数平面上に図示すると正六角形になります。
それぞれが
$\Phi_1(x), \Phi_2(x), \Phi_3(x), \Phi_6(x)$
のうち、どの円分多項式の材料になっているか図に書き入れてみます。
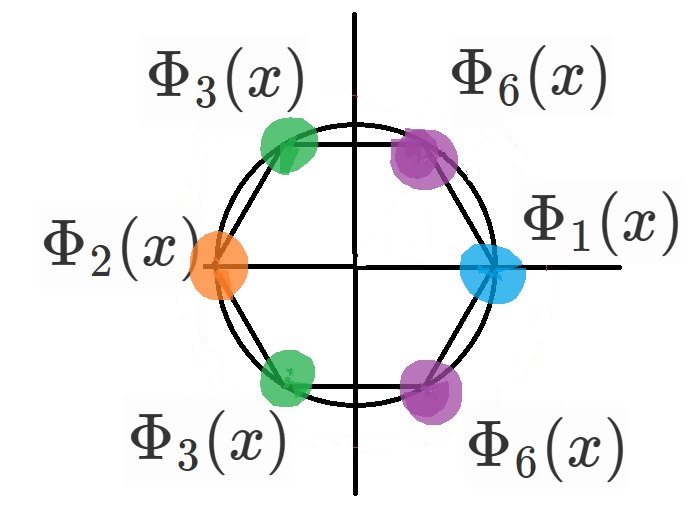
$\Phi_1(x)=x-\zeta_6^6$
$\Phi_2(x)=x-\zeta_6^3$
$\Phi_3(x)=(x-\zeta_6^2)(x-\zeta_6^4)$
$\Phi_6(x)=(x-\zeta_6)(x-\zeta_6^5)$
と分かります。
これから規則性をつかんでいきましょう。
もともと、円分多項式は最大公約数が1の奴らで構成されていたので、
指数と最大公約数に着目してみます。
$\Phi_6(x)$→$\zeta_6$と$\zeta_6^5$が材料→1と5は6との最大公約数が1(円分多項式の定義通り)
$\Phi_3(x)$→$\zeta_6^2$と$\zeta_6^4$が材料→2と4は6との最大公約数が2
$\Phi_2(x)$→$\zeta_6^3$が材料→3は6との最大公約数が3
$\Phi_1(x)$→$\zeta_6^6$が材料→6は6との最大公約数が6
なるほど。
$\Phi_6(x)$は6との最大公約数が1の奴らが材料ですが、1は$1=\dfrac{6}{6}$と捉えるとよさそうです。
同様にして議論を進めていきましょう。
$\Phi_3(x)$は6との最大公約数が2の奴らが材料です。$2=\dfrac{6}{3}$
$\Phi_2(x)$は6との最大公約数が3の奴らが材料です。$3=\dfrac{6}{2}$
$\Phi_1(x)$は6との最大公約数が6の奴らが材料です。$6=\dfrac{6}{1}$
これらのことから、
$\Phi_d(x)$を考える際は最大公約数を$g$としたときに、
$g=\dfrac{n}{d}$
の奴らだけ取り出して、
積を取ったやつが円分多項式となっていることを示せればよさそうです。
(証明)
$x^n-1=\Pi_{d|n}\Phi_d(x)$を示す。
いま、
$x^n-1=(x-\zeta_n)(x-\zeta_n^2)(x-\zeta_n^3)\cdots (x-\zeta_n^n)$
を積の記号$\Pi$を用いて
$x^n-1=\Pi_{k=1}^n(x-\zeta_n^k)$
と表す。
この左辺について、$k$と$n$の最大公約数が$g$であるものだけを集めて積をとったものを
$\Theta_g(x)=\Pi_{GCD(k, n)=g, 1<k<n}(x-\zeta_n^k)$
と置く。
$\Theta_g(x)$の定義と
$x^n-1=(x-\zeta_n)(x-\zeta_n^2)(x-\zeta_n^3)\cdots (x-\zeta_n^n)$
より、
$x^n-1=\Pi_{g|n}\Theta_g(x)$となる。
$g$は$k$と$n$の最大公約数なので、
$k=gk’$
$n=gd$
と置くことができる。
すると、
$k’=\dfrac{k}{g}$と
$d=\dfrac{n}{g}$
について、$d$は$n$の約数であり、$k’$は
$GCD(k’, d)=1, 1≦k’≦d$
を満たす。
また、
$\zeta_n^k=(\cos \dfrac{2\pi}{n}+\sin \dfrac{2\pi}{n})^k$
であり、ド・モアブルの定理から
$\zeta_n^k=\cos \dfrac{2k\pi}{n}+i\sin \dfrac{2k\pi}{n}$
である。
これに
$k=gk’$
$n=gd$
を代入すると、
$\zeta_n^k=\cos \dfrac{2k\pi}{n}+i\sin \dfrac{2k\pi}{n}$
$=\cos \dfrac{2gk’\pi}{gd}+\sin \dfrac{2gk’\pi}{gd}$
$=\cos \dfrac{2k’\pi}{d}+i\sin \dfrac{2k’\pi}{d}$
$=(\cos \dfrac{2\pi}{d}+i\sin \dfrac{2\pi}{d})^{k’}$
$=\zeta_d^{k’}$
が成り立つ。
$GCD(k’, d)=1, 1≦k’≦d$
であったので、
$\Theta_g(x)=\Pi_{GCD(k’, d)=1, 1≦k’≦d}(x-\zeta_d^{k’})$
となる。円分多項式の定義より、この式の右辺は$\Phi_d(x)$そのものである。
すると、$\Theta_g(x)=\Phi_d(x)$となり、
$d=\dfrac{d}{g}$に気を付けて
$x^n-1=\Pi_{g|n}\Theta_g(x)$に代入すると、
$x^n-1=\Pi_{d|n}\Phi_d(x)$
となる。
(証明終了)
円分多項式の性質② 整数係数多項式
(定理)
円分多項式
$\Phi_n(x)$は整数係数多項式である
これを示すにあたっては、
先ほど示した因数分解の性質
$x^n-1=\Pi_{d|n}\Phi_d(x)$
を使います。
また、この定理は$n$についての定理なので、
数学的帰納法を用います。
しかし、普通の帰納法ではなく、累積帰納法を用いますので、注意してください。
(証明)
数学的帰納法を用いて示す
$i)$ $n=1$のとき
円分多項式の定義より、$\Phi_1(x)=x-1$なので、これは整数係数多項式である。
$ii)$ $1≦k<n$ を満たす$k$に対して、$\Phi_k(x)$が整数係数多項式であると仮定する。
このとき、$\Phi_n(x)$が整数係数多項式であることを示す。
いま、円分多項式の性質①より、
$x^n-1=\Pi_{d|n}\Phi_d(x)\cdots ㋐$
である。
ここで、帰納法の仮定より、$1≦k<n$となる$k$については
$\Phi_k(x)$は整数係数多項式であるので、
㋐の右辺に登場する円分多項式のうち、$\Phi_n$以外のものは整数係数多項式である。
よって、㋐の右辺に登場する円分多項式のうち、$\Phi_n$以外の積によって定まる多項式を
$f(x)$とすると、$f(x)$も整数係数多項式である。
ここで、円分多項式はその定義より最高次の係数は1であるので、$f(x)$の最高次の係数も1である。
いま、
$x^n-1=f(x)\Phi_n(x)$
であるので、
$\Phi_n(x)$は$x^n-1$を$f(x)$で割り算することで得ることができる。
ここで、$x^n-1$は最高次の係数が1の整数係数多項式であり、
$f(x)$も最高次が1の整数係数多項式である。
最高次が1の整数係数多項式を、最高次が1の整数係数多項式で割った商も
整数係数多項式でなくてはならないので、
$\Phi_n(x)$は整数係数多項式である。
$i)$と$ii)$より、数学的帰納法から、全ての自然数$n$に対して
$\Phi_n(x)$は整数係数多項式である
(証明終了)
まとめ
いかがでしたか?
証明めっちゃ長かったですが、言いたいことは2つだけ。
・$x^n-1=\Pi_{d|n}\Phi_d(x)$
・円分多項式は整数係数多項式
のみです。
なんか今回の記事を書いていて、学生時代に数学書を読んだ時のことを思い出しました。
あの頃は、ある数学書を3行理解するのに19時間くらいかかってました笑(ノイキルヒのことです)
また次の記事でお会いしましょう!
コメント