和と差の積の因数分解の一般化から円分多項式へ

$x^2-1=(x-1)(x+1)$

中学３年生で因数分解を習って以来、入試問題で頻出の公式

和と差の積の因数分解。

数学Ⅱでは、これとよく似た公式

$x^3-1=(x-1)(x^2+x+1)$

を習います。

ここまできたら、

$x^4-1$や$x^5-1$を調べたくなるのが数学を愛する者の定めです。

観察→規則性を発見→証明です！！

和と差の積っぽい因数分解を観察

因数分解を実行するのは地味に結構大変なので、

今回はMaximaという数式処理システムの力を借りました。

結果を羅列すると、以下のようになります。

因数分解するときの係数の範囲は、有理数で考えていきます。

今回、めっちゃ面白いのでたくさん観察していきます！！

$x^2-1=(x-1)(x+1)$

$x^3-1=(x-1)(x^2+x+1)$

$x^4-1=(x-1)(x+1)(x^2+1)$

$x^5-1=(x-1)(x^4+x^3+x^2+x+1)$

$x^6-1=(x-1)(x+1)(x^2+x+1)(x^2-x+1)$

$x^7-1=(x-1)(x^6+x^5+x^4+x^3+x^2+x+1)$

$x^8-1=(x-1)(x+1)(x^2+1)(x^4+1)$

$x^9-1=(x-1)(x^2+x+1)(x^6+x^3+1)$

$x^{10}-1=(x-1)(x+1)(x^4+x^3+x^2+x+1)(x^4-x^3+x^2-x+1)$

$x^{11}-1=(x-1)(x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1)$

$x^{12}-1=(x-1)(x+1)(x^2+x+1)(x^2+1)(x^2-x+1)(x^4-x^2+1)$

$x^{13}-1=(x-1)(x^{12}+x^{11}+x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1)$

$x^{14}-1=(x-1)(x+1)(x^6+x^5+x^4+x^3+x^2+x+1)(x^6-x^5+x^4-x^3+x^2-x+1)$

これだけ観察すれば、具体例として十分です。

次は、これらの結果を基に規則性を見つけていきましょう！！

規則性を発見

まず、第一の感想として、

めっちゃ長い式がでるやつと、細かく因数分解できるやつがいる、

という点がもうすでに面白いです。

例えば、

$x^{13}-1=(x-1)(x^{12}+x^{11}+x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1)$

これヤバくないですか？

$x^{12}+x^{11}+x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1$

等比数列かよ！！と数学Bを習った人ならつっこみたくなることでしょう。

こんな長い式、入試問題の因数分解をやっているだけではまず出会わないです。

あんまり細かく因数分解できずに、長い式が出てくるやつらを集めてみましょう。

$x^3-1, x^5-1, x^7-1, x^{11}-1, x^{13}-1$

何か規則性はあるでしょうか？

そう。

全て素数です！！！

ここまでのことをまとめると、

$x^n-1$

の$n$が素数の場合は長い式が出てきて、

$n$が合成数の場合は細かく因数分解できる、

と分かりました。

素数の場合は掛け算で細かくできないけど、合成数は掛け算に分解できる。

なんかこれ、素因数分解に似ているな、というセンサーが働きます。

例えば、５や１１などの素数は、もうそれ以上素因数分解できませんが、

１２＝２×２×３

と、合成数は細かい掛け算に分解できます。

他に分かることはないでしょうか？

観察結果をよく見直してみると、全部の式が$(x-1)$を因数に持っていることが分かります。

$x-1$は共通ということですね。

他にもところどころ共通のものがありますね。

例えば、

$x^2-1$, $x^4-1$, $x^6-1$などには$x+1$が共通してます。

偶数ですね。

あと、

$x^3-1, x^6-1, x^9-1, x^{12}-1$には$x^2+x+1$

が共通しています。

これらは３の倍数です。

なんか、ますます素因数分解っぽいです。

全部に$x-1$が登場することは、こう解釈してみましょう。

$x^1-1=x-1$

なので、$x-1$は素因数分解における１のようなもので、別カウントなのだ、と。

そして、繰り返し出てくるやつらを記号で表していくことにします。

例えば、$x^1-1=x-1$は、$\Phi_1(x)=x-1$と表すことにします。

$x^2-1=(x-1)(x+1)$なので、

$x^2-1=\Phi_1(x)×(x+1)$

となります。

$x+1$は$x^n-1$の$n=2$で初めて出現する式なので、

$\Phi_2(x)=x+1$

と表すことにしましょう。

同じようなノリでいくと、

$x^3-1=\Phi_1(x)×(x^2+x+1)$

なので、

$\Phi_3(x)=x^2+x+1$と定義することになりそうです。

次は$n=4$の場合にいってみましょう。

$x^4-1=\Phi_1(x) \Phi_2 (x)×(x^2+1)$

なので、

$\Phi_4=x^2+1$

です。

以下、同様な感じで$\Phi_n$を定義していくと、先ほどの観察結果は次のように表記されます。

$x^1-1=\Phi_1(x)$

$x^2-1=\Phi_1 (x)\Phi_2(x)$

$x^3-1=\Phi_1(x) \Phi_3(x)$

$x^4-1=\Phi_1(x)\Phi_2(x)\Phi_4(x)$

$x^5-1=\Phi_1(x)\Phi_5(x)$

$x^6-1=\Phi_1(x)\Phi_2(x)\Phi_3(x)\Phi_6(x)$

$x^7-1=\Phi_1(x)\Phi_7(x)$

$x^8-1=\Phi_1(x)\Phi_2(x)\Phi_4(x)\Phi_8(x)$

$x^9-1=\Phi_1(x)\Phi_3(x)\Phi_9(x)$

$x^{10}-1=\Phi_1(x)\Phi_2(x)\Phi_5(x)\Phi_{10}(x)$

$x^{11}-1=\Phi_1(x)\Phi_{11}(x)$

$x^{12}-1=\Phi_1(x)\Phi_2(x)\Phi_3(x)\Phi_4(x)\Phi_6(x)\Phi_{12}(x)$

$x^{13}-1=\Phi_1(x)\Phi_{13}(x)$

$x^{14}-1=\Phi_1(x)\Phi_2(x)\Phi_7(x)\Phi_{14}(x)$

ヤバいですよね。

$\Phi_n(x)$の$n$の部分に約数がずらりと並んでいます。

例えば、１４の約数は１，２，７，１４ですが、

$x^{14}-1=\Phi_1(x)\Phi_2(x)\Phi_7(x)\Phi_{14}(x)$

です。

$\Phi_n(x)$に神秘を感ぜずにはいられません！！！

この驚くべき事実には過去の数学者も感動していて、

$\Phi_n(x)$には円分多項式という特別な名前がついています。

規則性を発見する段階のセクションでは、

円分多項式を具体例列挙方式で定義しました。

$\Phi_1(x)=x-1, \Phi_2(x)=x+1, \Phi_3(x)=x^2+x+1 \cdots$

といった感じです。

しかし、具体例列挙方式だと、

$\Phi_n(x)$は？

と聞かれた際に沈黙する他なくなってしまいます。

なのでここからは、具体例を一般化して、

円分多項式の正確な定義を与えていこうと思います。

円分多項式の定義をゲットしよう！

たいていの数学書では、円分多項式については定義が先に与えられているのですが、

今回は研究という視点を大切にしたいので、

円分多項式を再発見して我々で定義を与える、という過程を踏みたいと思います。

数学者が新しい数学の道具を生み出す過程を楽しんでみようぜ！という趣旨です。

円分多項式はそもそも$x^n-1$の因数分解に端を発しています。

これ、つまり１の$n$乗根を与える式じゃね？と気づければしめたもの。

$x^n-1=0$

について調べよう！という発想が生まれます。

これの重大な手掛かりは、ド・モアブルの定理です。

$x^n-1=0$の解は複素数平面上の正多角形になる、という事実が

円分多項式を考えていくうえで重要です。

例えば$n=3$の場合から順番に考えていきましょう。

$\Phi_3(x)=x^2+x+1$

ですが、$x^2+x+1=0$の解は$x=\dfrac{-1\pm \sqrt{3}i}{2}$

ですが、これは３次方程式の解の公式で出てきた$\omega, \omega^2$に他なりません。

複素数平面上に$x^3-1=0$の解

$\omega, \omega^2, \omega^3=1$

を図示すると、以下のようになります。

マーカーを付けた部分の解で$\Phi_3(x)$は作られています。

$\Phi_3(x)=(x-\omega)(x-\omega^2)=x^2+x+1$

次に$n=4$の場合を考えてみましょう。

$\Phi_4(x)=x^2+1$でしたが、

$x^2+1=0$の解は言わずと知れた$x=\pm i$です。

$x^4-1=0$の解は、あえて$i$だけで表すと

$x=i, i^2=-1, i^3=-i, i^4=1$

です。

これらを複素数平面上に図示すると図のようになります。

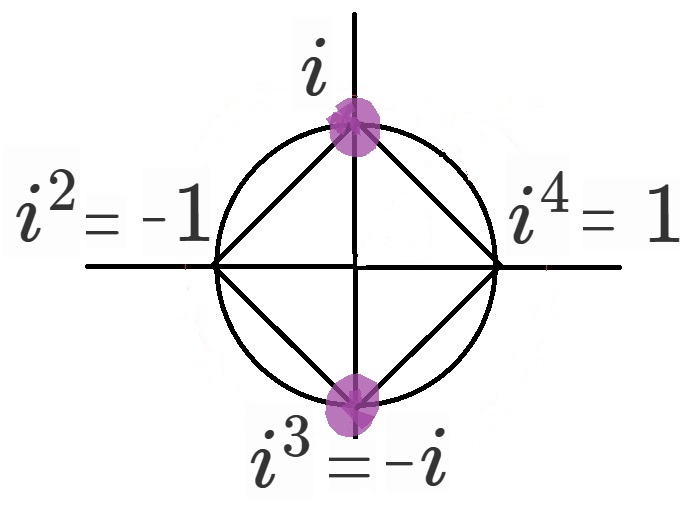
マーカーを付けた部分の解で$\Phi_4(x)$はできており、

$\Phi_4(x)=(x-i)(x-i^3)=x^2+1$

次は$x^5-1=0$です。

これの解で一番最初に出てくる虚数を$\zeta_5$と置きます。

$x^5-1=0$の解は、

$x=\zeta_5, (\zeta_5)^2, (\zeta_5)^3, (\zeta_5)^4, (\zeta_5)^5=1$です。

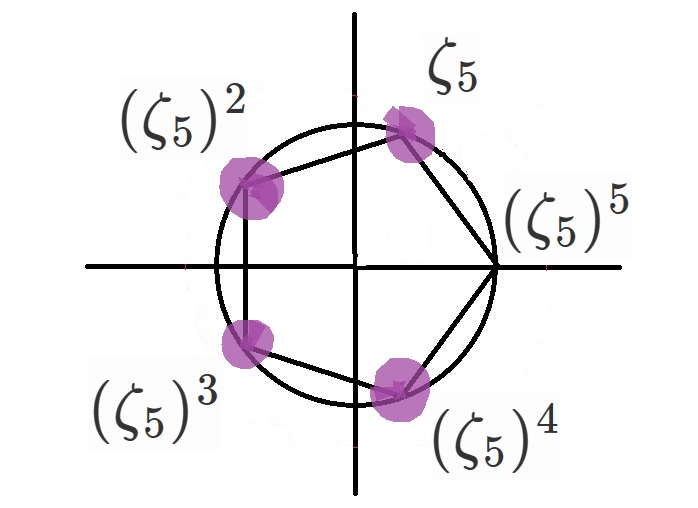
$\Phi_5(x)=(x-\zeta_5)(x-\zeta_5^2)(x-\zeta_5^3)(x-\zeta_5^4)$です。

ここまでくればおよそ規則性が見えてきた方も多いと思いますが、

それを確信に変えるため、$x^6-1=0$も観察していきます。

$x^6-1=0$の解で一番最初に出てくる複素数を$\zeta_6$とします。

$x^6-1=0$の解は

$x=\zeta_6, (\zeta_6)^2=\omega, (\zeta_6)^3=-1, (\zeta_6)^4=\omega^2, (\zeta_6)^5, (\zeta_6)^6=1$

です。

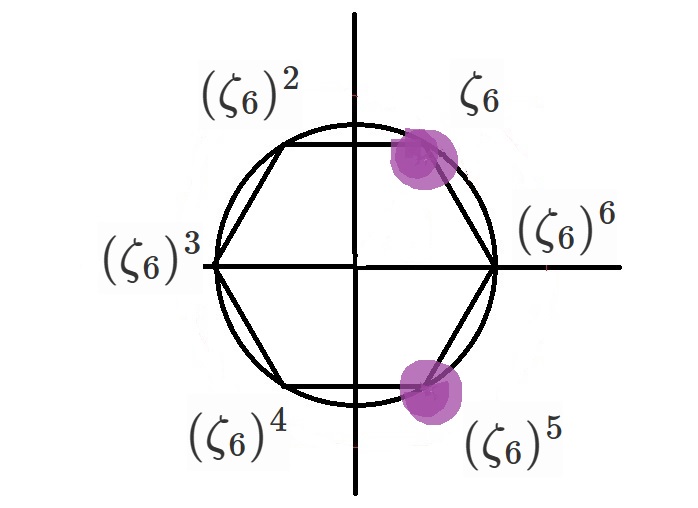
$\Phi_6(x)=(x-\zeta_6)(x-\zeta_6^5)=x^2-x+1$

です。さぁ、規則性は見抜けましたか？

キーワードは、互いに素です。

$x^n-1=0$の解で最初に出てくる虚数を$\zeta_n$とすると、$x^n-1=0$の解は

$x=(\zeta_n)^k$　$(k=1, 2, 3, \cdots, n)$

となります。

ここで、$k$が$n$と互いに素（最大公約数が１）になるものだけ取り出して

以下のようにしたものが円分多項式の正体です。

$\Phi_n(x)=(x-\zeta_n)×\cdots ×(x-\zeta_n^{n-1})$

例えば、$n=14$の場合を考えてみましょう。

$1≦k≦14$で、$14$と互いに素なのは、$k=1, 3, 5, 9, 11, 13$です。

よって、

$\Phi_{14}(x)=(x-\zeta_{14})(x-\zeta_{14}^3)(x-\zeta_{14}^5)(x-\zeta_{14}^9)(x-\zeta_{14}^{11})(x-\zeta_{14}^{13})$

となり、これを展開して整理したものが

$\Phi_{14}(x)=x^6-x^5+x^4-x^3+x^2-x+1$

という式だったのです。

これをもう少し専門的な記号を使って表すと、以下のようになります。

$\Phi_n(x)=\Pi_{GCD(n. k)=1, 1≦k≦n}(x-\zeta_n^k)$

$\Pi$は和の記号シグマの掛け算バージョンで、

$GCD(n. k)=1$は$n$と$k$の最大公約数は１だよ、という意味です

記号は本質的ではないので、さらっと流してください。

大切なのは、$x^n-1=0$の解のうち、

指数が$n$と互いに素な奴らだけ取り出して掛け算している、

という点です。

まとめ

いかがでしたか？

ほぼ大学数学の内容なので、難しく感じられたかもしれません。

ここまで読んでいただき、ありがとうございます！！

・$x^2-1=(x-1)(x+1)$を一般化すると円分多項式が出てくる

・$x^n-1=0$の解は$\zeta_n, (\zeta_n)^2, (\zeta_n)^3 \cdots, (\zeta_n)^k, \cdots, (\zeta_n)^n$

・$x^n-1=0$の解のうち、指数が$n$と互いに素なやつらだけ取り出して掛け算すると円分多項式になる

これらが今回の要点です。

円分多項式にはいろいろ興味深い性質があり、

ガロア理論でも結構本質的な立ち回りをするので、親しんでいただけたら幸いです。

ではまた次の記事でお会いしましょう！