群論を学んでいると、剰余類という概念が出てきます。
群論の脱落ポイントとして有名です(マスタの調べ)
しかし実はこの剰余類、すでに小学校の体育の授業で学んでいます。
今回は具体例を交えながら剰余類について解説していきます。
体育の授業しようぜ!
在りし日の体育の授業を思い浮かべてください。
今日の授業内容はバレーボール。
我々はウキウキで教室を飛び出し、体育館を走り回っています。

しかし各々が好き勝手に動き回っていては授業にならないので、
教員が指示を出しました。

「出席番号順で3列に整列!」
するとこのようになります。

始めに1班と2班が試合をし、3班は審判をすることになりました。
はい。
今回伝えたいことの本質的な説明は終了です!!
集合による記述
先ほどの体育の授業の例を集合を使って記述しなおそうと思います。
まず、体育をするクラスのメンバーは18人としましょう。
出席番号は1~18です。これを集合で
$A=\lbrace x \mid x= 1, 2, 3, 4, 5, \cdots, 18 \rbrace$
と表すことにします。
ここで、1班を$B_1,$ 2班を$B_2,$ 3班を$B_3$としましょう。
もちろん
$B_1=\lbrace 1, 4, 7, 10, 13, 16 \rbrace$
$B_2=\lbrace 2, 5, 8, 11, 14, 17, \rbrace$
$B_3=\lbrace 3, 6, 9, 12, 15, 18 \rbrace$
です。
これを文字で表しましょう。
$B_1=\lbrace 3m+1 \mid m=0, 1, 2, 3, 4, 5 \rbrace$
$B_2=\lbrace 3m+2 \mid m=0, 1, 2, 3, 4, 5 \rbrace$
$B_3=\lbrace 3m \mid m= 1, 2, 3, 4, 5, 6 \rbrace$
どうでしょう?文字を使って表すと、
$B_1$は3で割った余りが1である集まり
$B_2$は3で割った余りが2である集まり
$B_3$は3で割った余りが0である集まり(3の倍数の集まり)
となっていることが分かると思います。
要するに、「出席番号順で3列に整列!」という指示を数学的にとらえると、
「出席番号を3で割った余りが等しい人たちに分かれて!」ということなのです。
これによって
$A=B_1 \cup B_2 \cup B_3$
といったように、集合を分割することが可能になります。
3で割った余りで分類すると、集合を3つに分割できる。
当たり前の事実ですが、これが結構便利なのです。
余りに注目して分類しているので、
$B_1$や$B_2$や$B_3$を剰余類といいます。
剰余とは、余りのことなのです。
実は高校数学でも使っている剰余類の考え方
高校数学(特に大学入試の2次試験)では、剰余類の考え方が有効な問題が結構あります。
特に、整数問題で顕著です。
例えば、こんな問題があります
(問題)
全ての自然数$n$について、
$n^5-n$ が10の倍数であることを証明せよ
問題を解くときの思考回路を考えましょう。
まずこれは、「自然数$n$についての証明問題である」という解釈が大切です。
この時点で、証明の選択肢は大きく3つです
① $n$についての数学的帰納法
② 余りで分類して各個撃破
③ 背理法
②のやり方が剰余類による解法です。
今回は②の解法でこの問題を解いていきたいと思います。
まず、具体例を観察してみましょう。
$n^5-n$ に $n=2$を代入してみましょう。
$2^5-2=32-2=30$
30は10の倍数ですので、
$n=2$の場合は問題なく成立します。
$n=3$の場合はどうでしょうか?
$3^5-3=243-3=240$
240も10の倍数です。
$n=3$の場合でも問題なく成立します。
しかしこれをいくら続けていっても、
$n$は自然数全体で、無限個あるので、
全ての場合を証明したことにはなりません。
そこで、5で割った余りによる分類をします。
自然数を5で割った余りは、
0,1,2,3,4の5パターンしかありえません。
文字を使って表すと、
$n=5k, $ $5k+1,$ $ 5k+2,$ $5k+3,$ $ 5k+4$
の5パターンです。
今回の問題を「自然数についての証明問題」と捉えたままだと、
無限個の場合を永遠に確かめ続けないといけません。
しかし「自然数を剰余類で分類する」という発想があると、
今回の問題の場合は5パターンだけ調べればよいことになります。
このように、無限を有限に落とし込むことができるという点が剰余類の便利なところです。
では、解答に移っていきましょう。
(問題の解答)
全ての自然数$n$について
$n^5-n$が5の倍数であることを示す。
そのためには、$n^5-n$が2の倍数かつ5の倍数であることを示せばよい。
$n^5-n=n(n^4-1)$
$=n(n^2-1)(n^2+1)$
$=n(n-1)(n+1)(n^2+1)$
よって、
$n^5-n=n(n-1)(n+1)(n^2+1)$
である。
ここで、$n(n+1)$は連続する2つの自然数の積であるので、必ず2の倍数である。
ゆえに、$n^5-n$は2の倍数である$\cdots ②$
次に、$n^5-n$が5の倍数であることを示す。
以下では、$k$は自然数とする。
$n=5k$のとき
$n^5-n=n(n-1)(n+1)(n^2+1)$
であり、$n$が5の倍数であるので$n^5-n$は5の倍数となる$\cdots ㋐$
$n=5k+1$のとき
$n^5-n=n(n-1)(n+1)(n^2+1)$
について、$n-1$に着目する。
$n-1=(5k+1)-1=5k$
となるため、この場合$n-1$が5の倍数となる。
ゆえに$n^5-n$は5の倍数となる$\cdots ㋑$
$n=5k+2$のとき
$n^5-n=n(n-1)(n+1)(n^2+1)$
について、$n^2+1$に着目する。
$n^2+1=(5k+2)^2+1=(25k^2+20k+4)+1$
$=5(5k^2+4k+1)$
となり、この場合は$n^2+1$が5の倍数となる。
ゆえに$n^5-n$は5の倍数となる$\cdots ㋒$
$n=5k+3$のとき
$n^5-n=n(n-1)(n+1)(n^2+1)$
について、$n^2+1$に着目する。
$n^2+1=(5k+3)^2+1=(25k^2+30k+9)+1$
$=5(5k^2+6k+2)$
となり、この場合は$n^2+1$が5の倍数となる。
ゆえに$n^5-n$は5の倍数となる$\cdots ㋓$
$n=5k+4$のとき
$n^5-n=n(n-1)(n+1)(n^2+1)$
について、$n+1$に着目する。
$n+1=(5k+4)+1=5(k+1)$
となり、この場合は$n+1$が5の倍数となる。
ゆえに$n^5-n$は5の倍数となる$\cdots ㋔$
㋐㋑㋒㋓㋔より、$n^5-n$は5の倍数である$\cdots ②$
①と②より、$n^5-n$は2の倍数かつ5の倍数であるので、10の倍数である
(証明終了)
このように、剰余類の考え方は無限個の場合を証明しないといけない問題を有限個のパターンに落とし込むことができるというメリットがあり、高校数学(大学入試)で知らず知らずのうちに使われています。
次の見出しでは、剰余類を群の概念を用いてもう少し詳しく見ていこうと思います
剰余類を群で捉える
ここの見出しでは「群」という概念と「部分群」という概念を使います。
初めに定義だけ述べておこうと思います。
(群の定義)
集合$G$にある演算$〇$が定義されているとする。
$G$が以下の条件を満たすとき、$G$を群(ぐん)という
①すべての$a, b, c \in G$について、$a〇 (b〇 c)=(a〇 b)〇 c$が成り立つ
(結合法則)
②すべての$a \in G$に対して、$ae=ea=a$となる$e \in G$が存在する
($e$を単位元という)
③すべての$a \in G$に対して、$ax=xa=e$となる$x \in G$が存在する
($x$を逆元という)
(部分群の定義)
集合$G$は演算〇について群となっているとする。
$G$の部分集合$H$が次の3つの条件を満たすとき、
$H$を$G$の部分集合という。
① $a, b \in H$ならば、$a〇 b \in H$
② $a \in H$ならば、$a^{-1} \in H$
③ $H$は空集合ではない
「群」ってなんだよ!なんでこんなもん考える意味があるの?
「部分群」の定義ってなんでこんな条件になっているの?
といったことに興味を持たれた方は、ぜひ以下の記事をご覧ください。


さて、ここから剰余類について群の視点で考えていこうと思います。
剰余類は新しい概念です。
数学で新しい概念をゲットするときは、
「具体例 → 一般化して定義をゲット」
という流れがとても大切です。
そこで今回は、
まず整数$\mathbb{Z}$と3で割った余りを例に説明をしていこうと思います。
整数を3で割った余りで分類する例
まず、整数$\mathbb{Z}=\lbrace \cdots, -2, -1, 0, 1, 2, 3, \cdots \rbrace$
が群であるかどうか考えます。
群を考える際には、「どの集合について考えるか」と「どの演算につて考えるか」の2点が大切です。
整数全体の集合$\mathbb{Z}$の場合は掛け算×については群になりません。(逆元がない)
しかし、足し算+については群となります。
整数全体の集合$\mathbb{Z}$は「足し算」について群になっている
ということをまず押さえておきましょう。
ここで、3で割った余りを考えるので、まず3の倍数全体の集合を考えます。
$X=\lbrace 3m \mid m \in \mathbb{Z} \rbrace$
としましょう。
まず、$X$が$\mathbb{Z}$の部分集合であることは明らかです。
問題は、$X$が$\mathbb{Z}$の部分群になっているかどうか。
それを足し算+に着目して確かめていきましょう。
まず、(3の倍数)+(3の倍数)=(3の倍数)
は問題なく成立するので、$X$は足し算について閉じています$\cdots ①$
また、$3a \in X$を適当にとると、$-3a \in X$も成り立ち、
$3a+(-3a)=0$
であることから逆元も存在します$\cdots ②$
そして$X$は空集合ではありません$\cdots ③$
①②③より、$X$は$\mathbb{Z}$の部分群となっています。
ちなみに、$X=\lbrace 3m \mid m \in \mathbb{Z} \rbrace$
ですが、これは整数を3倍してできる集合なので、素朴に
$X=3\mathbb{Z}$
と表すことがあります。
次に3で割って1余るやつら全体の集合を考えましょう。
$Y=\lbrace 1+3m \mid m \in \mathbb{Z} \rbrace$
とします。
(なぜ$3m+1$ではなく$1+3m$としているかに気が向いた方は鋭いです!が今はまぁ慣例でそうなっているくらいで流してください。+は交換法則が成立しますので気にしなくてよいのです)
(3で割って1余る数)+(3で割って1余る数)=(3で割って2余る数)
なので、$Y$は$\mathbb{Z}$の部分群ではありません。
$Y=\lbrace 1+3m \mid m \in \mathbb{Z} \rbrace$
は「1と(3の倍数)を足しているもの」と解釈できるので、
$Y=1+3\mathbb{Z}$
と表すことがあります。
同じように3で割って2余るやつら全体の集合を考えます。
$W=\lbrace 2+3m \mid m \in \mathbb{Z} \rbrace$
とします。
(3で割ると2余る数)+(3で割ると2余る数)=(3で割ると4余る数)=(3で割ると1余る数)
なので、$W$も$\mathbb{Z}$の部分群にはなりません。
$W=\lbrace 2+3m \mid m \in \mathbb{Z} \rbrace$
は「2と(3の倍数)を足しているもの」と解釈できるので、
$W=2+3\mathbb{Z}$
と表すことがあります。
一般に、
$x, n \in \mathbb{Z}$に対して、
集合$\lbrace x+nm \mid m \in \mathbb{Z} \rbrace$を
$\lbrace x+nm \mid m \in \mathbb{Z} \rbrace=x+n\mathbb{Z}$
と表します。
さぁ、ここからが本題です。
整数を3で割った余りは絶対に
0,1,2,以外にはありえないので、
$\mathbb{Z}=X \cup Y \cup W$
のように$\mathbb{Z}$を3つの集合に分割できます。
$X=3\mathbb{Z},$ $Y=1+3\mathbb{Z},$ $W=2+3\mathbb{Z}$
を踏まえると、
$\mathbb{Z}=3\mathbb{Z} \cup (1+3\mathbb{Z}) \cup (2+3\mathbb{Z})$
となります。
ここで、
$\lbrace 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z} \rbrace$
という集合を考えましょう。
これは剰余類を集めた集合です。
群$\mathbb{Z}$を、部分群$3\mathbb{Z}$を使って3つに分けていることになります。
これがあたかも割り算の余りの計算かのように見えるので、
$\lbrace 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z} \rbrace$を
$\lbrace 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z} \rbrace =\mathbb{Z}/3\mathbb{Z}$
と表します。
イメージ的には、
$x+n\mathbb{Z}→剰余類$
$\mathbb{Z}/n\mathbb{Z}→剰余類でできた集合$
といった感じです。
また、
$1+3\mathbb{Z}$は3で割った余りが1である奴ら全体の集合ですが、
ちょっと書くのがめんどくさいので、
$1+3\mathbb{Z}=\bar{1}$
と表すことがあります。
同じように、
$2+3\mathbb{Z}=\bar{2}$
と表すことがあります。
$3\mathbb{Z}$の場合は、
$3\mathbb{Z}=0+3\mathbb{Z}$
なので、
$3\mathbb{Z}=\bar{0}$
と表すことがあります。
すると、
$\mathbb{Z}/3\mathbb{Z}= \lbrace 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z} \rbrace $
を
$\mathbb{Z}/3\mathbb{Z}=\lbrace \bar{0}, \bar{1}, \bar{2} \rbrace$
と表すことができます。
意味的には、
(3で割った余り)=(余り0と 余り1と 余り2です)
といった感じです。
すごくすっきり表すことができるのです。
剰余類や剰余類の集合を考える際は、記号で躓く人が多いので(僕のこと)、
各記号が何を表してるかを見失わないようにしておきましょう。
剰余類の一般化
さて、先ほどの例では
「足し算+についての群$\mathbb{Z}$」に対して
「3$\mathbb{Z}$」という部分群を考えました。
そして$3\mathbb{Z}$を使って
$1+3\mathbb{Z}, 2+3\mathbb{Z}$という剰余類を作り、
剰余類の集合
$\mathbb{Z}/n\mathbb{Z}=\lbrace 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z} \rbrace$
というものを考えた、という流れでした。
これを一般化していきます。
オレンジマーカー、黄色マーカー、緑マーカーのそれぞれの手順を順に一般化していきましょう。
まずはオレンジマーカーからです。
まず、「足し算+についての群$\mathbb{Z}$」という文言を一般化しましょう。
群の演算は常に足し算とは限らないので、この部分は
「演算〇 についての群$G$」とでもしておきましょうか。
〇には定義可能な演算ならなんでも入れてよいわけです。
「+」でも「×」でも「写像の合成」でもOK!
「$3\mathbb{Z}$」は「$G$の部分群$H$」とすればすぐ一般化できます。
次は黄色マーカーです。
$1+3\mathbb{Z}, 2+3\mathbb{Z}$
はどう一般化するとよいでしょうか?
まず、$1+3\mathbb{Z}$についてもう少し詳しく考えましょう。
$1+3\mathbb{Z}=\lbrace 1+3m \mid m \in \mathbb{Z} \rbrace$
でした。
要するに、
$\lbrace 1+3m \mid m \in \mathbb{Z} \rbrace$
を$G$と$H$で置き換えていけばよいわけです。
いま、$G$は$\mathbb{Z}$に対応し、$H$は$3\mathbb{Z}$に対応しています。
$1+3m$に着目しましょう。
$1+3m$ を $1$ と $3m$ に分けて考えます。
$1\in \mathbb{Z}$で、$3m \in 3\mathbb{Z}$ではないですか?
ということは、
$1$ → $G$の元$g$
$3m$ → $H$の元$h$
+ → 〇
のように置き換えるとうまく一般化できそうです!
$H$による$G$の剰余類は、
ある$g \in G$を固定して、
$\lbrace g〇h \mid h \in H \rbrace$
と定めることにしましょう。
$1+3\mathbb{Z}$に習って
$1$ → $g$
+ → 〇
$3\mathbb{Z}$ → $H$
と置き換えると、
$\lbrace g〇h \mid h \in H \rbrace$は
$\lbrace g〇h \mid h \in H \rbrace =g 〇 H$
と表すのがよさそうです。
僕ならこうするのですが、数学の慣例では〇を省略する流れがあるので、
この記事でも慣例に従って$g 〇 H$を$gH$と表すことにします。
で、実はこれ、$g$が$H$の左側にあるというのが結構重要なのです。
なぜかというと、
群では可換法則が成立しないから。
一般には$gH \neq Hg$
なのです。
(場合によっては$gH =Hg$な成り立つこともありますが、すごくレアケースです)
そこで、$gH$ と $Hg$ を区別するため、
$gH$を左剰余類
$Hg$を右剰余類
といいます。$g$が右にいるか左にいるかで名前が変わるのです。
一度ここまでの内容をまとめておきましょう。
(左剰余類の定義)
群$G$と、その部分群$H$があり、$g \in G$をとる。
$\lbrace g〇h \mid h \in H \rbrace$
を$H$による$G$の左側剰余類といい、
$gH$で表す。
ちなみに、$H$による$G$の左剰余類を全てあつめた集合を
$G/H$で表します。
あえて表すなら、$G/H$の元は集合で、みな$gH$のような形をしていますから、
$G/H=\lbrace aH \mid a\in G\rbrace$
となります。
これは$\mathbb{Z}/3\mathbb{Z}$に相当するやつです。
3次の対称群の剰余類
さぁ、剰余類を一般化できたので、新たな例を観察しましょう!
例として使うのは、おなじみ3次の対称群$S_3$です!
$S_3$は3つの並べ替え全体の集合が織りなす群で、
3!=6個の元を持ち、
写像の合成に関する群であります。
6つの元を具体的に書き下すと、

の6つです。
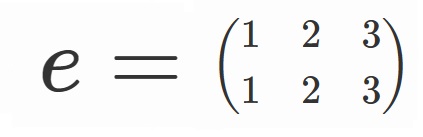
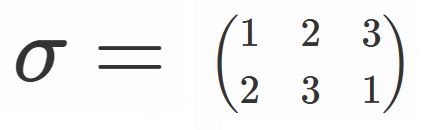
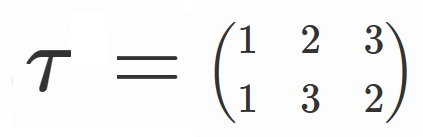
とすると、
$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$
と表されます。そしてこれは並べ替え(写像)の合成〇について群となります。
$S_3$は3次方程式が解ける理屈を解明するときに大活躍しました。
$S_3$の活躍に興味がある方は以下の記事をご覧ください。
さて、$S_3$の剰余類を考えるにあたっては、$S_3$の部分群が必要になります。
$S_3$の部分群はいろいろあるのですが、今回は
$A_3=\lbrace e, \sigma, \sigma^2 \rbrace$
を考えましょう。
$A_3$が本当に$S_3$の部分群になっているのかどうかは以下の記事の具体例の見出しをご覧ください。

部分群を決定する際には、ラグランジュの定理というものがとても便利なので、
そのうち別の記事で解説しようと思います。ご期待ください。
さて。
剰余群を考えましょう。
$A_3$に何か$S_3$の元を左から掛ける(合成する)のです。
$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$
で、
$A_3=\lbrace e, \sigma, \sigma^2 \rbrace$
です。
ここからは、$S_3$の演算表を使って頑張って剰余類を計算していきましょう!

$S_3$の元は6つあるので、一つずつ$A_3$にかけていきます。
まずは$e$からです。
$eA_3=\lbrace e〇a \mid a \in A_3 \rbrace$
$=\lbrace e〇e, e〇\sigma, e〇\sigma^2 \rbrace$
ここで演算表より、
$e〇e=e,$ $e〇\sigma=\sigma,$ $e〇\sigma^2=\sigma^2$
なので、
$eA_3=\lbrace e, \sigma, \sigma^2 \rbrace$
です。ここで、$A_3=\lbrace e, \sigma, \sigma^2 \rbrace$
だったので、$eA_3=A_3$です。
次に$\sigma A_3$を考えましょう。
$\sigma A_3=\lbrace \sigma 〇e, \sigma 〇\sigma, \sigma 〇\sigma^2 \rbrace$
$=\lbrace \sigma, \sigma^2, e \rbrace$
$=A_3$
したがって、$\sigma A_3=A_3$です。
同様に、$\sigma^2 A_3=A_3$が確かめられます。
次に、$\tau A_3$を考えましょう。
$\tau A_3=\lbrace \tau 〇 e, \tau 〇 \sigma, \tau 〇 \sigma^2 \rbrace$
$=\lbrace \tau, \tau \sigma, \tau \sigma^2 \rbrace$
これ以上は計算できないので、
$\tau A_3$は$\tau A_3$のままです。
次に$\tau \sigma A_3$を考えます。
$\tau \sigma A_3=\lbrace \tau \sigma 〇 e, \tau \sigma 〇\sigma, \tau \sigma 〇\sigma^2 \rbrace$
$=\lbrace \tau \sigma, \tau \sigma^2, \tau \rbrace$
$=\tau A_3$
よって、$\tau \sigma A_3 =\tau A_3$です。
同様に、$\tau \sigma^2 A_3=\tau A_3$となることが確認できます。
6通り全て試した結果、$A_3$による$S_3$の剰余類は$A_3$と$\tau A_3$のみであると分かりました。
ここで、
$\mathbb{Z}/3\mathbb{Z}=\lbrace 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z} \rbrace$
と同じようにして$S_3/A_3$を考えると、
$S_3/A_3=\lbrace A_3, \tau A_3 \rbrace$
となります。
ちなみに、$S_3/A_3$は
3次方程式が解ける仕組みを対称性で説明しようとした際に突然登場したなぞの集合でしたが、
ここで伏線回収されました。
$S_3$の部分群$A_3$で剰余類を考えた結果でてきたものが$S_3/A_3$だったわけです。
$S_3/A_3$の活躍については以下の記事をご覧ください。

まとめ
いかがでしたか?
・剰余類とは、「出席番号順で3列に整列!」を一般化したもの
・剰余類を集めた集合を$G/H$と表す
の2点をおさえていただければと思います。
さて、今回出てきた$G/H$ですが、
まれにこれが群としての構造を持つ場合があります。
次回の記事ではどのような条件を付けると$G/H$は群になるのだろう?
ということを考えていきたいと思います。
ご期待ください。
参考
画像素材提供:Peggy und Marco Lachmann-AnkeによるPixabayからの画像

コメント