群の定義のなぜに答える試み

代数学を学んでいると、必ず「群」という概念と出会います。

天下り的に定義を覚えることから出発しがちですが、

なんであんな定義になっているのか、必然性を疑問に思う方も多いと思います。

そこで、今回の記事では、体（たい）との比較という視点で群の定義に迫っていこうと思います

群（ぐん）誕生の背景

群（ぐん）という概念は、５次方程式が解けない仕組みを調べる過程で発見された概念です。

ざっくり流れをまとめると、

①方程式を解くとは、解を係数と根号で表すこと（係数の世界をひろげること）

②解を求める際には、対称式の基本定理と、解と係数の関係のコンボがとても有効で、解を使ったうまい対称式を見つけることができると（ラグランジュ・リゾルベントを使う）、とても嬉しい。

③そのため、対称性を計る物差しのようなものが必要

④解の並べ替えを考え、どの並べ替えで不変となるかで対称性を調べていた（すべての並べ替えで不変ならそれは対称式）

⑤並べ替えについて調べてみよう！

というモチベーションです。

ここまでの流れについて更に詳細に知りたい方はぜひ以下の記事をご覧ください

そして、並べ替えについて研究を進めていった先に群（ぐん）という概念と出会うこととなります。

では、とりあえず定義を述べようと思います。

おそらくこんな感想を持たれたのではないでしょうか？

は？と。

多分、初見では何が何やらさっぱりです（経験者は語る）

大抵の代数学の教科書では、

まず群（ぐん）のことを学び、次に環（かん）について学び、最後に体（たい）を紹介します。

しかしこれがめちゃくちゃ分かりにくい！！

群の定義が天下り的に与えられても、なんとなくキツネにつままれたような感覚になります。

ひとまず定義を受け入れ、具体例で慣れ親しみ、問題演習を積めば大学の単位は取れますが、

なんか釈然としない！

なんでそんな定義にしようと思ったか昔の数学者に聞きたい！

という思いがありました。

色々と試行錯誤した結果、

あ、これ、先に体（たい）を説明した方がいいんじゃね？

という境地に至りましたので、

今回の記事では従来の

群（ぐん）→環（かん）→体（たい）

という順番ではなく、

体（たい）→群（ぐん）

という順番で解説をしようと思います。

体（たい）について

ここでは、体（たい）という概念が何のためのもので、

どういう定義なのかを考えていきたいと思います。

群（ぐん）の定義を考えるにあたって、なぜ先に体（たい）を考えるのか？

それは先ほどの見出しで確認した、

群が登場する流れの第一ステップを見ると分かります。

①方程式を解くとは、解を係数と根号で表すこと（係数の世界を広げること）

これです。これをもう少し詳しく見ていきましょう。

例えば、

$x^2-5x+6=0$

を解くときには、因数分解で解きます。

$x^2+5x+6=0$

$(x-2)(x-3)=0$

$x=2, 3$

となります。

$x^2-5x+6=0$

の係数は有理数$\mathbb{Q}$で、解である$x=2, 3$も有理数なので、

今回は係数の世界を広げなくとも因数分解を進めることができて、解を求めることができます。

しかし、

$x^2-3=0$

ではそうはいきません。

$x^2-3=0$

の係数は有理数ですが、有理数係数の範囲では

$x^2-3=0$

はこれ以上因数分解できません。既約です。

これを

$x^2-3=(x-\sqrt{3})(x+\sqrt{3})$

のように因数分解するためには、

係数の範囲を有理数$\mathbb{Q}$から$\mathbb{Q}(\sqrt{3})$まで広げないといけません。

ちなみに、$\mathbb{Q}(\sqrt{3})=\lbrace a+b\sqrt{3} \mid a, b \in \mathbb{Q} \rbrace$です。

このように、方程式を解く作業は、係数の世界を広げる作業を捉えなおすことができます。

ここで、係数の世界への考察を深めるために体（たい）という考え方が登場します。

通常、方程式の係数を考える際には、有理数$\mathbb{Q}$からスタートします。

なぜかというと、そうしないと1次方程式ですら解けないからです。

たとえば、

$2x+1=0$を解いてみましょう。

$2x+1=0$

の係数の範囲は整数です。

まず移項しましょう。

$2x=-1$

問題は次です。解を得るためには両辺を２で割らないといけません。

$x=-\dfrac{1}{2}$

ここで、$-\dfrac{1}{2}$は整数ではありません。有理数です。

ゆえに、方程式の係数は有理数からスタートするのが普通です。

要するに、１次方程式を解くためにあたって、

係数は割り算について閉じていてほしいわけです。

自然数$\mathbb{N}=\lbrace 1, 2, 3, \cdots \rbrace$

は足し算と掛け算について閉じていますが、引き算と割り算については閉じていません。

整数$\mathbb{Z}=\lbrace \cdots -3, -2, -1, 0, 1, 2, 3, \cdots, \rbrace $

は足し算、引き算、掛け算については閉じていますが、割り算で閉じていません。

有理数$\mathbb{Q}=\lbrace \dfrac{b}{a} \mid a, b, \in \mathbb{Z} \rbrace$

になって初めて、足し算、掛け算、引き算、割り算すべての四則演算で閉じた集合になります。

しかし、四則演算について閉じている集合は、有理数だけではありません。

例えば、

$\mathbb{Q}(\sqrt{3})=\lbrace a+b\sqrt{3} \mid a, b \in \mathbb{Q} \rbrace$

も四則演算で閉じています。

（↑割り算について閉じていることを確認するために有理化を使います。詳しくは以下の記事をご覧ください）

要するに、方程式の係数について考えるにあたっては、

四則演算で閉じている

ということがすごく大切なわけです。

こうして、四則演算で閉じているものについて調べてみようかな？というモチベーションが生まれます。

まずは観察から始めましょう。

有理数$\mathbb{Q}$はどんな計算法則を満たすでしょうか？

まず、有理数は足し算について閉じています。

また、足し算について結合法則が成り立ち、

$a, b, c \in \mathbb{Q}$について$a+(b+c)=(a+b)+c$となります。

また、足し算について交換法則が成り立ち、

$a+b=b+a$となります。

そして、引き算についても閉じていますが、例えば

$\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1}{2}+(-\dfrac{1}{3})$

ととらえると、実質的に引き算は負の数を足していると捉えることができます。

ゆえに、足し算について確認したことを改めて引き算について確認する必要はありません。

しかし、足し算と引き算についてはまだ議論の余地があります。

方程式について考えているので、

例えば$x+a=0$が解けるかどうか確認しなければなりません。

無論、移項すれば$x=-a$であることはすぐに分かりますが、

もう少し丁寧に式変形をしていきましょう。

移項とはつまり、両辺に$(-a)$を足すことに他なりません

$x+a+(-a)=0+(-a)$

$x+0=-a$

$x=-a$

です。

上記の式変形を実現するためには、

$0$が$0+a=a$を満たすことと、

どの$a$に対しても

$a+(-a)=(-a)+a=0$となる$-a \in \mathbb{Q}$が存在すること

が必要です。

ひとまず足し算と引き算については以上です。

次に掛け算について考えましょう。

掛け算についても結合法則と交換法則が成り立ち、

$a(bc)=(ab)c$

$ab=ba$

です。

割り算については、例えば

$5÷2=5×\dfrac{1}{2}=5×2^{-1}$

と捉えることができます。

「$÷2$」は　「$×2^{-1}$」　ですので、割り算は実質的には掛け算です。

なので、掛け算について確認したことを改めて割り算でも確認する必要はありません。

（$2^{-1} \in \mathbb{Q}$であることがとても重要）

あとは、例えば$3x+2=0$

が解けないといけません。

$a+(-a)=(-a)+a=0$となる$-a \in \mathbb{Q}$が存在することから、両辺に-2を足すことができ、

$3x=-2$です。これを解くには両辺を３で割ればいいですが、少し丁寧に変形すると、

$3x=-2$

$3^{-1}×3×x=3^{-1}×(-2)$

$1×x=\dfrac{1}{3}×(-2)$

$x=-\dfrac{2}{3}$

です。これを実現させるためには、

$1$が$1×x=x×1=x$

を満たすことと、

$0$以外のどんな$a$に対しても$a^{-1}\in \mathbb{Q}$が存在することが必要です。

これで掛け算と割り算については以上です。

あと、中学１年生で習う通り、有理数では分配法則が成り立ちます。

$a(b+c)=ab+bc$

と

$(a+b)c=ac+bc$

です。これも大切な性質です。

そのほか、有理数$\mathbb{Q}$に特有の性質もありますが、

とりあえず今まで述べた性質があれば１次方程式を解くことができるので、

これらを満たす集合を体（たい）と呼ぶことにします。

では、次の見出しで群について考えていきましょう！

群（ぐん）について

さて、ここからいよいよ群という概念が登場します。

５次方程式が解けないことを示すためには、対称性に着目して方程式を観察する必要がありました。

その際、対称性を計る道具として「並べ替え」が重要です。

例えば、２次方程式の場合を考えます。

いま、$a, b, c$を有理数とし、

$ax^2+bx+c=0$

の解を$x=x_1, x_2$とします。

解が２つであり、$x_1$と$x_2$の並べ替えは２！＝２通りです。

具体的には、

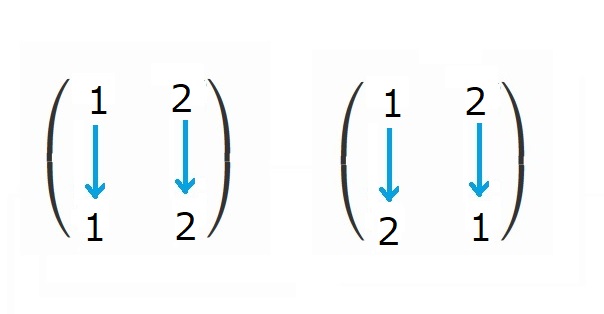
の２通りです。

例えば、$x_1+x_2$はこの２つの並べ替えで不変であり、対称式です。

ここで、$x_1-x_2$を考えてみましょう。

（ちなみにこれを２次のラグランジュ・リゾルベントというのでした）

これに先ほどの並べ替えを作用させると、

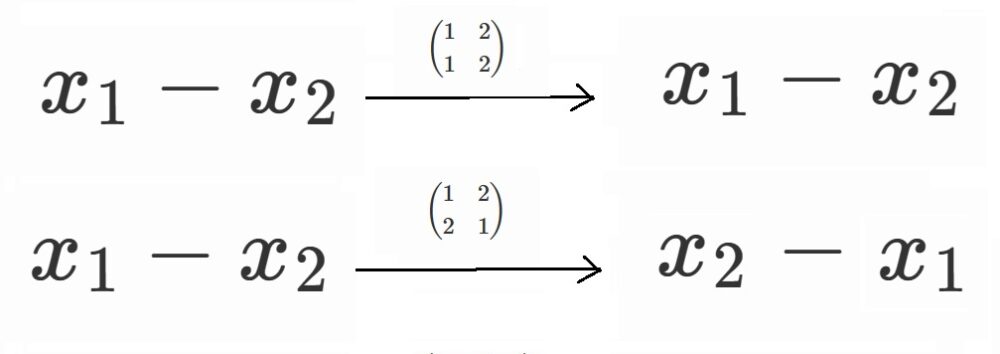
となります。

$x_1-x_2 \neq x_2-x_1$

なので、これは対称式ではありません。

しかし、二乗して$(x_1-x_2)^2$にすると、

これは２！通りのすべての並べ替えで不変であり、対称式となります。

二乗することで対称性を上げることができるわけです。

対称式の基本定理より、対称式は基本対称式で表すことができます。

ここで、解と係数の関係より、

$x_1+x_2=-\dfrac{b}{a}$

$x_1x_2=\dfrac{c}{a}$

だったので、基本対称式は元の方程式の係数で表されます。

よって、

$(x_1-x_2)^2$

は元の方程式の係数で表されることになります。

実際、

$(x_1-x_2)^2=(x_1+x_2)^2-4x_1x_2$

$=(\dfrac{b}{a})^2-4\dfrac{c}{a}$

$=\dfrac{b^2-4ac}{a^2}$

したがって、

$(x_1-x_2)^2=\dfrac{b^2-4ac}{a^2}$

となり、両辺２乗根をとると、

$x_1-x_2=\pm \dfrac{\sqrt{b^2-4ac}}{a}$

です。

ここで、

$x_1+x_2=-\dfrac{b}{a}$

$x_1-x_2=\pm \dfrac{\sqrt{b^2-4ac}}{a}$

の連立方程式を解くと、

$x_1, x_2=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

となり、解の公式が導かれます。

３次方程式の場合は３！＝６通りの並べ替え

について考えることになり、

４次方程式の際には４！＝２４通りの並べ替え

について考えることになりました。

めっちゃ面白いので、詳細な内容は以下をご覧ください。

方程式を研究していく中で、対称性という視点が重要であり、並べ替えについて調べてみよう！

というモチベーションが生まれたわけです。

並べ替えは、数や図形や関数しか調べてこなかったガロア理論以前の数学界にとって新たな研究対象。

新たな研究対象を手に入れたとき、どういう姿勢が大切かというと、

今までの研究対象と比べて、何が新しいのかを知るということに尽きます。

例えば、方程式を調べるうえでは、初めは係数の世界をどう広げるかという発想で

四則演算で閉じていることが大切

ということに気が付き、体という概念を手に入れました。

「体」と「並べ替え」はどこが同じで、どこが違うのだろう？

といったことを抽象的に考えていくことになります。

ひとまず、３つの並べ替え全体$S_3$について考えていきましょう。

$S_3$の元は３！＝６通りあり、具体的には

です。

ここで、

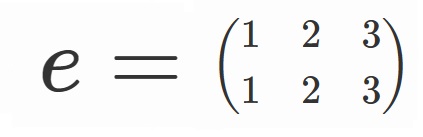
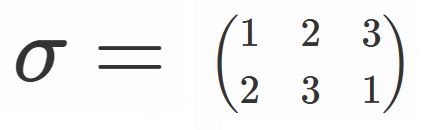
と置くことにします。

ここで、３次のラグランジュ・リゾルベントである

$x_1+\omega x_2+\omega^2 x_3$

を考えます。

$x_1 +\omega x_2 + \omega^2 x_3$に$\sigma$を作用させることを

$\sigma (x_1+\omega x_2+\omega^2 x_3)$

とかくことにしましょう。

すると、

$\sigma (x_1+\omega x_2+\omega^2 x_3)=x_2+\omega x_3 +\omega^2 x_1$

となります。これは$\sigma$という並べ替えの定義そのものなので、当たり前と言えば当たり前です。

ここで、

$x_2+\omega x_3 +\omega^2 x_1$

にもう一度$\sigma$を作用させてみましょう。

$\sigma (x_2+\omega x_3+\omega^2 x_1)=x_3+\omega x_1 +\omega^2 x_2$

要するに、

$x_1 + \omega x_2 +\omega^2 x_3$に

$\sigma$を２回作用させると

$x_3+\omega x_1 +\omega^2 x_2$になるということです。

並べ替えを続けて行うことは「写像の合成」と捉えることができます。

今回の「$\sigma$を２回作用させる」という操作は、普通は写像の合成の記号を用いて

$\sigma 〇 \sigma$

と表しますが、これを$\sigma 〇 \sigma=\sigma^2$と表すことにしましょう。

すると、

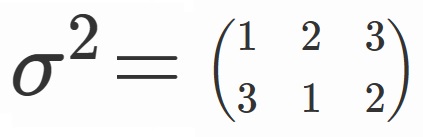
となることが先ほどの議論から分かります。

ちなみに、

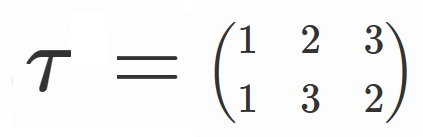
と置くことして、$\tau 〇 \sigma$を単に$\tau \sigma$と表すことにすると、

$S_3$の６つの元たちは

$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$

となることが確認されます。

これを踏まえたうえで、「体」と「並べ替え」の違いを考えていきます。

体の定義をおさらいしましょう。

まず、体は加法と乗法という２つの演算で閉じた集合です。

しかし、$S_3$には写像の合成（乗法っぽく振る舞う）しか演算がありません。

ゆえに体の９つの条件のうち、

加法が関わってくる①、②、③、④、⑨はそもそも成り立ちません。

よって、⑤、⑥、⑦、⑧について議論していくことになります。

さて、そもそも$S_3$は写像の合成に関して閉じているのでしょうか？

それを１００マス計算のような感じで計算して確かめてみましょう。

これは実際に計算して確かめるしかありませんが、結果をまとめると以下のようになります。

上記の表を演算表といいます。

演算表から、計算結果には$S_3$の６種類の元しか出現していないので、

$S_3$が写像の合成について閉じていることが分かります。

ここで、、$e$が関わる計算結果だけ取り出してみると、

例えば$\sigma e =e \sigma=\sigma$

が成り立つことが分かります。

つまり、体の条件⑦でいう$1$に相当する役割を$e$が担っているのです！

演算表より、すべての$a \in S_3$に対して$a e=e a=a$となり、

$e \in S_3$であるので、$S_3$は⑦の条件は満たすことになります。

体との共通点です。

ここで、演算表のうち、

$\tau \sigma$　と　$\sigma \tau$

の計算結果は特筆に値するので、少し丁寧に確認をしようと思います。

$\sigma (x_1+\omega x_2 +\omega^2 x_3)=x_2+\omega x_3+\omega^2 x_1$

ここで、$\tau (x_2+\omega x_3+\omega^2 x_1)=x_3+\omega x_2+\omega^2 x_1$

よって、$\tau 〇 \sigma (x_1+\omega x_2+\omega^2 x_3)=x_3+\omega x_2+\omega^2 x_1$

また、$\tau (x_1+\omega x_2+\omega^2 x_3)=x_1+\omega x_3+\omega^2 x_2$

ここで、$\sigma (x_1+\omega x_3+\omega^2 x_2)=x_2+\omega x_1+\omega^2 x_3$

よって、$\sigma 〇 \tau =x_2+\omega x_1+\omega^2 x_3$

すなわち、

$\tau 〇 \sigma(x_1+\omega x_2+\omega^2 x_3) \neq \sigma 〇 \tau (x_1+\omega x_2+\omega^2 x_3)$

であり、$\tau \sigma \neq \sigma \tau$

なのです。

$S_3$では、交換法則が成り立たない！！

次に条件⑧に着目しましょう。

$S_3$の６つの元それぞれに、$ax=xa=e$となる$x$（つまり逆元）が存在するかどうか調べます。

まず$e$について。

演算表より、$e 〇 e=e$なので、$e$自身が$e$の逆元となります。

順次他の元についても演算表を使って確認していきましょう。

$\sigma$　→　$\sigma 〇 \sigma^2 =\sigma^2 〇 \sigma =e$

　　　　　　　　$\sigma^2$が逆元

$\sigma^2$　→　$\sigma^2 〇 \sigma=\sigma 〇 \sigma^2 =e$

　　　　　　　　$\sigma$が逆元

$\tau$　→　$\tau 〇 \tau =e$

　　　　　　　　$\tau$自身が逆元

$\tau \sigma$　→　$\tau \sigma 〇 \tau \sigma =e$

　　　　　　　　$\tau \sigma$自身が逆元

$\tau \sigma^2$　→　$\tau \sigma^2 〇 \tau \sigma^2=e$

　　　　　　　　$\tau \sigma^2$自身が逆元

以上のことより、$S_3$は全ての元に逆元が存在するため、条件⑧も満たします。

最後に結合法則を確認しましょう。

演算表を参考に、　

$\tau 〇 (\tau \sigma 〇 \sigma^2)$ 　と　$(\tau 〇\tau \sigma)〇 \sigma^2$　

を計算してみようと思います。

$\tau 〇 (\tau \sigma 〇 \sigma^2)=\tau 〇 \tau \sigma^2=\sigma$

$(\tau 〇\tau \sigma)〇 \sigma^2=\sigma^2 〇 \sigma^2 =\sigma$

よって、$\tau 〇 (\tau \sigma 〇 \sigma^2)=(\tau 〇\tau \sigma)〇 \sigma^2$

となり、これが全ての元で成り立つので、$S_3$は結合法則を満たし、条件⑤を満たすことが分かります。

以上をまとめると、

$S_3$は体の条件９つのうち、⑤と⑦と⑧のみを満たし、①②③④⑨は満たさないことが分かりました。

そこで、⑤と⑦と⑧のみを満たす集合に

新たに群（ぐん）と呼ぶことにしましょう！！！

体の場合と違って、

群は交換法則が成り立たない

という事実はとても重要なので、ぜひ頭の片隅にとどめておいてください。

ちなみに、体を考える際も群を考える際も結合法則の確認は結構大切なのですが、

その意義はちょっと分かりにくいと思うので、それを補足しておきます。

これは、なぜ結合法則を考える必要があるか、という視点で考えるよりも、

結合法則がない世界ではどんな困った事態が起こるか、

といった視点で考えた方が分かりやすいように感じます。

要するに、「結合法則がない世界」と「結合法則がある世界」を比べてみるわけです。

ひとまず、結合法則が成り立たない世界を考えましょう。

当然、

$a(bc) \neq (ab)c$

です。３つの掛け算くらいなら、そこまで不便さはないかもしれませんが、

例えば４つの掛け算を考える際に結構ヤバいことになります。

$a(bc)d, (ab)(cd), (ab(cd)) \cdots$

は全て異なる値をとる可能性がありますので、

いちいちすべての値を計算して検討しなければなりません。

とんでもなく面倒くさいです。

ところが、結合法則が成り立つ世界では、

$a(bc)d=(ab)(cd)=(ab(cd))=abcd$

ですから、これらは全て同じ値となり、極めて簡素で計算が考えやすくなります。

このように、定義に必然性を感じない条件がある場合は、

それがない場合とある場合を比較してみるという視点が大切になります。

まとめ

いかがでしたか？

方程式を調べていく過程で「体（たい）」という概念と「並べ替え」に出会い、

「体（たい）」と「並べ替え」を比較することで「群（ぐん）」の定義を与えるという試みでした。

何かの参考となれば幸いです。

ではまた次回の記事でお会いしましょう！

次の記事

参考

画像素材提供（アイキャッチ）：TooDoTATによるPixabayからの画像