今回は円分多項式の既約性の証明の完全バージョンを紹介します。
今まで素数次の場合と素数のべき乗次の場合をやってきましたが、
ここにきてついに一般の場合です。
円分多項式の既約性は数論においてマジで超重要な結果です。
ですが、証明が超めんどくさいことでも有名です。
なんなら「証明は参考文献を参照」としている数学書もあるくらいです。
今回の記事では、この円分多項式の既約性を
なるべく分かりやすく、なぜその式変形をするのかといった発想の部分まで解説します。
分かりやすさと丁寧さを重視した結果、簡素さの対極へたどり着きましたので、
式変形の意味も含めて円分多項式の既約性を理解したい!という方以外はブラウザバックしてください
円分多項式とは?
そもそも円分多項式とは何だったでしょうか?
おさらいしておきましょう
(既知な方は読み飛ばして次の見出しに進んでOKです)
それは、
$x^n-1=0$
という方程式から生まれました。
例えば$n=2$のとき
$x^2=(x-1)(x+1)$です。
$n=3$
なら
$x^3-1=(x-1)(x^2+x+1)$
です。
このように、$x^n-1$を因数分解したときに現れる多項式が円分多項式です。
ではなぜ円分多項式という名前がついているのでしょう?
それは、$x^n-1=0$の解を複素平面上に図示すると分かります。
たとえば、$x^5-1=0$の解を図示すると次のようになります
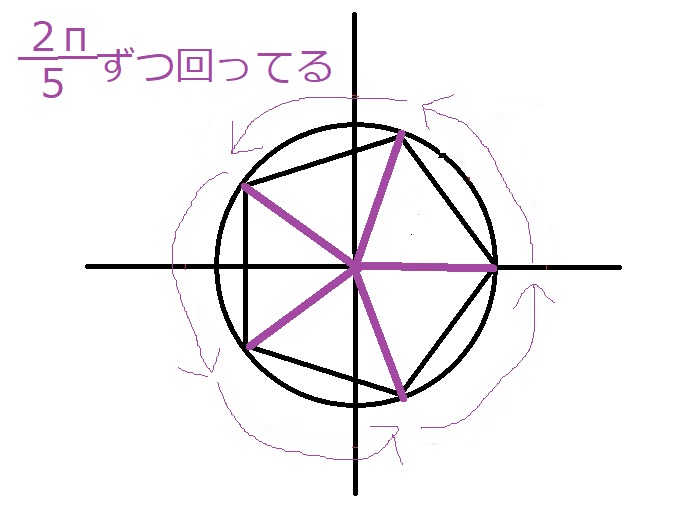
この正五角形の各頂点が$x^5-1=0$の解です。
これらを具体的に書き下すと、
$\zeta_5=\cos \dfrac{2\pi}{5}+i\sin \dfrac{2\pi}{5}$
を用いて
$x=\zeta_5, \zeta_5^2, \zeta_5^3, \zeta_5^4, \zeta_5^5(=1)$
となります。
一般に$x^n-1=0$
を考える場合、解は
$\zeta_n=\cos \dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$
を用いて
$x=\zeta_n^k$ $(k=1, 2, \cdots, n)$
と表されます。
これら$\zeta_n^k$のうち、
$n$と$k$が互いに素なものを1の原始n乗根と呼びます
円分多項式は、1の原始n乗根のみを解に持つ多項式のことです。
以上を数式で表現すると、以下のようになります。
(定義)
$\zeta_n=\cos \dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とする。
このとき、
$\Pi_{GCD(n, k)=1, 1≦k≦n}(x-\zeta_n^k)$
を円分多項式といい、$\Phi_n(x)$で表す
この円分多項式については、
特筆すべき特徴がいくつかあります。
(円分多項式の特徴①)
$x^n-1=\Pi_{d|n}\Phi_d(x)$
が成り立つ
これは結構ヤバい性質です。
$n=6$の場合を確認しましょう。
6の約数は1,2,3,6です。
ところで、$x^6-1$を因数分解すると、
$x^6-1=\Phi_1(x)\Phi_2(x)\Phi_3(x)\Phi_6(x)$
となります。ヤバくないですか?
$x^n-1$の因数分解は、$n$の約数次の円分多項式の積だよ!
というビックリ定理です。
また、円分多項式は必ず整数系巣の多項式となります。
(円分多項式の性質②)
円分多項式$\Phi_n(x)$は
整数係数多項式である
なにをそんな当たり前のことを、と思うかもしれませんが、これは結構すごい主張です。
円分多項式の定義を思い出してみましょう
$\Pi_{GCD(n, k)=1, 1≦k≦n}(x-\zeta_n^k)$
です。
$\zeta_n=\cos \dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$
という超やばい複素数が多数登場しているにもかかわらず、展開して整理すると整数係数になるよ、
ということを主張しているのです。
円分多項式の性質①と②の証明ってどうなってるんだ?と興味をもたれた方は以下の記事をご覧ください
そして、円分多項式の著しい、もっとも重要な性質が次です
(円分多項式の性質③)
円分多項式$\Phi_n(x)$は
整数係数の範囲で既約である
そう。
円分多項式の性質②では、整数係数だよ、というところまでしか主張できません。
たとえば、
$\Phi_5(x)=x^4+x^3+x^2+x+1$
です。整数係数です。
でも、ひょっとしたらまだ因数分解できるかもしれません。
「円分多項式が整数係数である」と「円分多項式が整数係数の範囲で既約である」
はまったく別次元の主張なのです。
今までは段階的にこの既約性に取り組んできました。
まずは$n$が素数の時を示しました。
たとえば、$\Phi_3(x)$とか、$\Phi_5(x)$とか、$\Phi_7(x)$とか、
こいつらはみんな整数係数の範囲で既約だよ!と証明済みです。
次に、$n$が素数のべき乗の場合を証明しました
$\Phi_9(x)$とか、$\Phi_{27}(x)$とか、$\Phi_{25}(x)$とか、
こういうのも全部整数係数の範囲で既約だよ!と証明済みです。
がしかし、
たとえば$\Phi_{12}(x)$とか$\Phi_{100}(x)$とか、
$n$が一般の自然数の場合はまだ既約性を証明できていません。
そこで今回は、この一般の場合の円分多項式が整数係数の範囲で既約であることを証明します。
$n$が素数の場合と$n$が素数のべき乗の場合の証明に興味をもっていただけた方は以下の記事をご覧ください。
アイゼンシュタインの既約判定法と、その改造版が大活躍します。


円分多項式の既約性の証明のための準備
一般の円分多項式の既約性の証明はマジで大変です。
ほんとに果てしなき長編小説のクライマックスに存在しているといっても過言ではありません。
ここでは、そんな長編小説の随所で活躍する登場人物たちを紹介します
便宜上、定理A、B、C…みたいな感じで名前を割り振っていこうと思います。
(定理A:対称式の基本定理)
$n$この文字の多項式
$f(\alpha_1, \alpha_2, \cdots, \alpha_n)$
が対称式である場合、それは基本対称式
$s_1, s_2, \cdots, s_n$の多項式
$g(s_1, s_2, \cdots, s_n)$
で表すことができる
いきなり章ボス級の大物が登場です。
なんか難しい表現をしていますが、要するに対称式は基本対称式で表せるよ、
という内容です。
証明に興味がある方は以下の記事をご覧ください

(定理B:多項定理)
$(x_1+x_2+\cdots +x_n)^m$
を展開したときの$x_1^{e_1}x_2^{e_2}\cdots x_m^{e_n}$
の係数は$\dfrac{m!}{e_1!e_2!\cdots e_n!}$
となる。
ただし、
$0≦e_i$ $i=1, 2, \cdots, n$
$e_1+e_2+\cdots +e_n=m$
多項定理は二項定理の応用バージョンとして、入試数学でもたまに使います。
(定理C)
$p$を素数とする。
このとき、
$\dfrac{p!}{e_1!e_2!\cdots e_n!}$
は$p$の倍数となる。
($0≦e_i$ $i=1, 2, \cdots, n$
$e_1+e_2+\cdots +e_n=p$)
(定理Cの証明)
$0≦e_i$ かつ $e_1+e_2+\cdots +e_n=p$であるので、
$\dfrac{p!}{e_1!e_2!\cdots e_n!}$
は必ず自然数である。よって、$A$を自然数として、
$\dfrac{p!}{e_1!e_2! \cdots e_n!}=A$
とおくことにする。
$p×(p-1)!=A×e_1!e_2! \cdots e_n!$
である。
左辺は$p$の倍数であるので、右辺も$p$の倍数でなければならない。
ここで、$e_1+e_2+\cdots +e_n=p$と$0≦e_i$より、
$0≦e_i<p$ $i=1, 2, \cdots, n$
である。
したがって、$e_1!e_2!\cdots e_n!$
は$p$と互いに素であり、$A$が$p$の倍数でなければならない。
(証明終了)
まだまだ続きます。
(定理D:フェルマーの小定理)
$p$が素数で$a$が整数のとき、
$a^p \equiv a(\mod p)$
が成り立つ
これまた超大物登場です。
フェルマーの小定理は、
$a^{p-1}\equiv 1(\mod p)$
という式が本来の姿ですが、
今回はこれの両辺を$a$倍した形で使います。
証明に興味がある方は以下の記事をご覧ください

まだまだ続きます。
(定理E:微分の公式)
$n$が自然数の時、
$(x^n)’=nx^{n-1}$
となる。
ただし$’$は微分の記号を表す
(定理F:積の微分公式)
$f(x)$と$g(x)$について、
$\lbrace f(x)g(x) \rbrace ‘=f'(x)g(x)+f(x)g'(x)$
となる。
ただし$’$は微分の記号を表す
(定理G)
$f(x)$と$g(x)$について、
$\lbrace f(g(x)) \rbrace’ =f'(g(x))g'(x)$
となる。
ただし$’$は微分の記号を表す
微分についての詳しい内容はまた別の記事で深く掘り下げようと思いますので、
今回はさらりと流してください。
多項式の因数分解の話でなぜ微分が出てくるの?と疑問に思われた方もいると思いますので、
軽くだけ微分を使う意味を補足しようと思います。
まず、
$(x^n)’=nx^{n-1}$
を見て欲しいのですが、
$x^n$は係数が1で、次数はnです
これを微分すると
$nx^{n-1}$となりますが、これは係数がnで、次数がnー1です。
要するに、微分することによって係数と次数を調節することができます。
これが多項式の既約性を扱うにあたって結構便利なのです。
あとは、既約多項式の性質をいくつか使います。
(定理H)
$f(x)$を$\mathbb{Q}$上の既約多項式とする。
また、$g(x)$は有理数係数多項式とする。
このとき、$f(x)=0$と$g(x)=0$が共通の解を一つでももてば、
$g(x)$は$f(x)$で割り切れる。
(定理I)
$f(x)$を$\mathbb{Q}$上の既約多項式とする。
また、$g(x)$は有理数係数多項式とする。
このとき、$g(x)$の次数が1次以上で、かつ$f(x)$の次数よりは小さければ、
$f(x)=0$と$g(x)=0$
は共通の解を持たない。
(定理J)
$f(x)$を$\mathbb{Q}$上の既約多項式とする。
$f(x)=0$は重解をもたない。
既約多項式の性質について、証明がきになった方はぜひ以下の記事をご覧ください。
既約多項式の性質を一覧表にしてまためてあります。

円分多項式の既約性の証明
満を持して、円分多項式の既約性を証明していきます。
(定理:円分多項式の既約性)
円分多項式$\Phi_n(x)$は
整数係数の範囲で既約である。
証明はとてつもなく長い旅になります。
高度な数学を使うのではなく、素朴な発想を大切にしたかったのです。
長いですが、もし最後までお付き合いいただけたのなら。
それは幸甚です。
(証明)
$\zeta_n=\cos \dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とする。
$x^n-1=0$
の解は
$x=\zeta_n, \zeta_n^2, \cdots. \zeta_n^n(=1)$
である。
$\Phi_n(x)$は定義より、先ほどの
$\zeta_n^k$ $(k=1, 2, 3, \cdots, n)$
のうち、$n$と$k$が互いに素となるものだけを解に持つ。
ここで、$k=1$の場合である$x=\zeta_n$を
解にもつ既約多項式$f(x)$を考える。
$\Phi_n(x)$と$f(x)$はともに$x=\zeta_n$
を解に持つので、定理Hより、
$f(x)$は$\Phi_n(x)$を割り切る。
ここで円分多項式の性質②より、
$\Phi_n(x)$は整数係数の多項式であり、最高次の係数は1であるので、
$f(x)$も最高次が1の整数係数多項式でなければならない。
そこで、
$f(x)=x^m+a_{m-1}x^{m-1}+\cdots +a_1x+a_0$
とおく。
$f(x)$が$\Phi_n(x)$と一致することを示したい。
そのためには、$f(x)$が$x=\zeta_n$のみならず、
$x=\zeta_n^k$ ($1≦k≦n$で、かつ$k$は$n$と互いに素な数)
を全て解に持つことを示せればよい。
そこで、$p$を$n$と互いに素な$n$より小さい素数として、
$f(x)$が$x=\zeta_n^p$を解に持つことをまず示していく。
いま、$f(x)$を$m$次の多項式と置いているので、
$f(x)=0$は$m$個の解をもつ。
この$m$個の解を
$\alpha_1, \alpha_2, \cdots, \alpha_m$
とし、$\alpha_m=\zeta_n$とする。
すなわち、
$f(x)=(x-\alpha_1)(x-\alpha_2)\cdots (x-\alpha_m)$
である。
ここで、$f(x)=0$の$m$個の解を$p$乗したものを解に持つ多項式$\psi(x)$を考える。
$\psi(x)=(x-\alpha_1^p)(x-\alpha_2^p)\cdots (x-\alpha_m^p) \cdots ①$
である。
$\psi(x)$が整数係数多項式であることをここで確認する。
ひとまず、$\psi(x)$の係数を文字で置き、
$\psi(x)=x^m+A_{m-1}x^{m-1}+\cdots +A_1x+A_0$
と表すことにする。
$\psi(x)$について、①の右辺を展開して整理すると、
解と係数の関係より、
$A_i$ ($i=0, 1, 2, \cdots, m-1$)
は$\alpha_1^p, \alpha_2^p, \cdots, \alpha_m^p$の対称式になる。
つまりは$\alpha_1, \alpha_2, \cdots, \alpha_m$の対称式である。
したがって、定理A(対称式の基本定理)から、
$A_i$は$\alpha_1, \alpha_2, \cdots, \alpha_m$の基本対称式で表される。
ここで、$\alpha_1, \alpha_2, \cdots, \alpha_m$の基本対称式とは、
$f(x)$の係数で表されるものに他ならない。(←プラスかマイナスかの違いは発生します)
ゆえに、$A_i$は整数$a_1, a_2, \cdots, a_{m-1}$の多項式で表されるので、整数である。
以上のことから、$\psi(x)$は整数係数多項式である。
ここで、$f(x)$の係数$a_{m-1}$と$\psi(x)$の係数$A_{m-1}$に着目する。
$a_{m-1}=-(\alpha_1+\alpha_2 +\cdots +\alpha_m)$
$A_{m-1}=-(\alpha_1^p+\alpha_2^p+\cdots +\alpha_m^p)$
である。
ここで、
$(\alpha_1+\alpha_2 +\cdots +\alpha_m)^p$
を考える。
定理Bと定理Cより、
$(\alpha_1+\alpha_2 +\cdots +\alpha_m)^p$
を展開した時の係数について、
$\alpha_1^p, \alpha_2^p, \cdots, \alpha_m^p$
以外の項の係数は全て$p$の倍数である。これをまとめて
$(\alpha_1+\alpha_2 +\cdots +\alpha_m)^p=\alpha_1^p+\alpha_2^p+\cdots +\alpha_m^p+pM$
とおくことにする($a_{m-1}$が整数であるためには、$M$は整数でなければならない)
すると、
$(\alpha_1+\alpha_2 +\cdots +\alpha_m)^p \equiv \alpha_1^p+\alpha_2^p+\cdots +\alpha_m^p(\mod p)$
となり、すなわち
$(-a_{m-1})^p\equiv -A_{m-1}(\mod p)\cdots ②$
である。
ここで、
左辺$(-a_{m-1})^p$について、定理D(フェルマーの小定理)より、
$(-a_{m-1})^p \equiv -a_{m-1}(\mod p)\cdots ③$
であった。
②と③より、
$a_{m-1}\equiv A_{m-1}(\mod p)$
となる。
他の係数についても同様であるので、
$f(x)$と$\psi (x)$は$p$を法として合同である$\cdots ④$
ここで、$f(x)=\psi(x)$であれば、
$f(x)$が$x=\alpha_1^p$を解に持つことになり、
つまりは$x=\zeta_n^p$を解に持つことになる。
ゆえに、ここからは$f(x)=\psi(x)$を示す。
背理法によって示す。
$f(x) \neq \psi(x)$と仮定する。
すると、
$\psi(x)-f(x)\neq 0$
となる。
④より、$f(x)$と$g(x)$は$p$を法として合同であるので、
ある整数係数多項式$G(x)$が存在して、
$\psi(x)-f(x)=pG(x)$
となる。
ゆえに
$\psi(x)=f(x)+pG(x)$
である。
ここで、$f(x)$は既約多項式なので、定理Jより重解を持たない。
ここで、$\psi(x)$も重解をもたないでいてほしいので、
それを示す。
仮に$\alpha_i^p =\alpha_j^p$であるとする($i<j$)。
すると、$p$の定義より$p$と$n$は互いに素であるので、法$n$において$p$は必ず逆元をもつ
その逆元を$s$と置くと、$ps \equiv 1(\mod n)$である。
ここで、$\alpha_i^p =\alpha_j^p$の両辺を$s$乗する。
$\alpha_i^{ps}=\alpha_j^{ps}$
である。
いま、$\alpha_i, \alpha_j$は$x^n-1=0$の解であったので、
$ps \equiv 1(\mod n)$であるなら
$\alpha_i^{ps}=\alpha_1$かつ
$\alpha_j^{ps}=\alpha_j$
である。
ゆえに$\alpha_i=\alpha_j$
であるが、これは$f(x)$が重解を持たないことに矛盾する。
よって、$\psi(x)$も重解を持たない。
いま、$f(x) \neq \psi (x)$と仮定しており、
$f(x)$は既約多項式であるので、定理Iより、
$f(x)$と$\psi(x)$は共通の解をもちえない。
以上のことより、$f(x)$の解と$\psi(x)$の解は、全て相違なる1のn乗根でなければならない。
したがって、$f(x) \psi(x)$が$x^n-1$の因数となる。これを
$x^n-1=f(x)\psi(x)P(x) \cdots ⑤$
と表すことにする。($P(x)$は整数係数多項式)
⑤に$\psi(x)=f(x)+pG(x)$を代入する。
$x^n-1=f(x)×(f(x)+pG(x))×P(x)$
$x^n-1=f(x) ^2×P(x)+pf(x)×G(x)×P(x)$
簡略のため、
$f(x)×G(x)×P(x)=Q(x)$
とおく。$Q(x)$は$n-1$次以下の整数係数多項式である
$x^n-1=f(x)^2×P(x)+pQ(x)$
である。
この両辺を$x$で微分する。定理Eと定理Fと定理Gより、
$nx^{n-1}=2f(x)f'(x)P(x)+f(x)P'(x)+pQ'(x)$
$nx^{n-1}=f(x)×\lbrace f'(x)P(x)+P'(x)\rbrace +pQ'(x)$
となる。簡略のため、
$f'(x)P(x)+P'(x)=R(x)$とおく。
$R(x)$は$n-1$次以下の整数係数多項式である。
$nx^{n-1}=f(x)R(x)+pQ'(x)$
となる。
ここで、$Q'(x)$は$n-2$次以下の整数係数多項式である。
$nx^{n-1}=f(x)R(x)+pQ'(x)$
より、
$nx^{n-1}-pQ'(x)=f(x)R(x)$
である。
$n$と$p$は互いに素であるので、
左辺は最高次の係数のみ$p$の倍数ではなく、
最高次以外の係数は全て$p$の倍数である。
ゆえに$f(x)$も最高次の係数以外は$p$の倍数でなくてはならない。
これを今から示す。
(ここからアイゼンシュタインのときと同じような超長い議論タイムが始まります。
黄色マーカーまで読み飛ばしてもOKです。むしろそうしてください)
「$f(x)$の最高次の係数以外のある係数が$p$の倍数にならないか、
または$R(x)$の最高次以外の係数のある係数が$p$の倍数にならない」と仮定する.
いま、
$f(x)=a_mx^m+a_{m-1}x^{m-1}+\cdots +a_1x+a_0$
である。($a_m=1$です)
$R(x)$を$u$次の多項式とし、
$R(x)=r_ux^r+r_{u-1}x^{u-1}+\cdots r_1x+r_0$
とおく。
$m+t=n-1$である。
$f(x)$の最高次の係数以外のある係数のうち、$p$の倍数とならない最小のものが$j$次の係数$a_j$ $(0≦j<m)$だったとする。
$nx^{n-1}-pQ'(x)=f(x)R(x)$
について、$j+u$次の係数を考えると、
$a_{j+u}r_0+\cdots a_{j+1}r_{u-1} +a_jr_u \cdots ⑤$
となる。
(計算してみると分かりますが、添え字の和が$j+u$になるやつらを足すことになります)
⑤について
$a_j$の定義より、$a_{j+1}, a_{j+2}, \cdots, a_{j+u}$
は全て$p$の倍数でなければならない。
したがって、左辺の
$a_{j+u}r_0+\cdots a_{j+1}r_{u-1} $
は$p$の倍数である。
簡略のため、これを$pD$とおく $(Dは整数)$
すると、⑤は
$pD+a_jr_u\cdots ⑥$
となる。
ここで、
$nx^{n-1}-pQ'(x)=f(x)R(x)$
の左辺に着目すると。
⑥は$p$の倍数である。
⑥について、$pD$も$p$の倍数であるので
$a_{j}r_u$も$p$の倍数でなければならない。
ここで、$a_j$の定義より、これは$p$の倍数ではない。
また、$r_u$は$R(x)$の最高次の係数のため、これも$p$の倍数ではない。
($nx^{n-1}-pQ'(x)=f(x)R(x)$について、最高次の係数を比較すると
$n=a_mr_u$で$n$が$p$と互いに素だからです)
ゆえに、$a_jr_u$は$p$の倍数になりえないが、これは矛盾。
よって、
「$f(x)$の最高次の係数以外のある係数が$p$の倍数にならないか、
または$R(x)$の最高次以外の係数のある係数が$p$の倍数にならない」という仮定が間違っていた
ということになり、背理法より
「$f(x)$の最高次の係数以外の任意の係数が全て$p$の倍数で、
かつ$R(x)$の最高次以外の係数以外の任意の係数も全て$p$の倍数である」
ということになる。
ゆえに$f(x)$の定数項は$p$の倍数であることになる。
しかし、$f(x)$は1のn乗根のみを解に持つ整数係数多項式であるので、
定数項は$1$か$-1$でなければならない。←(普通の係数は整数なら何でもいいですが、定数項は$1$か$-1$です)
これは矛盾である。
ゆえに、$f(x)\neq \psi(x)$が間違っていたことになり、
背理法から$f(x)=\psi(x)$となる。
以上のことから、$\Phi_n(x)$の解$x=\zeta_n$について、
$f(x)$が$x=\zeta_n$を解に持つ既約多項式であるときは
$f(x)$の解の$p$乗を解にもつ多項式$\psi(x)$を考えることによって
$f(x)$が$x=\zeta_n^p$も解に持つことが分かった。
いま、$f(x)$が$\Phi_n(x)$の解を全て解にもつことを示したいのであった。
$\Phi_n(x)$の解とはつまり
$x=\zeta_n^k$ ($n$と$k$は互いに素)
である。
いま、$k$が$k=pp_1p_2p_3\cdots p_t$
のように因数分解されているとする。
(素因数は重複を許します。例えば$12=2^2×3$ですが、$12=2×2×3$のように表すということです)
すると、ここまでの議論で$f(x)$は$x=\zeta_n^p$を解に持つことが分かっているので、
$\psi(x)$を考えたときと同様に$f(x)$の解の$p_1$乗を解としてもつ多項式
$\psi_1(x)$を考えれば、これまでと同様の議論によって
$f(x)$は$x=\zeta_n^{pp_1}$を解に持つことになる。
これを繰り返していけば、ついには$f(x)$は
$x=\zeta_n^k$を解に持つことになり、
$\Phi_n(x)$の解を全て解に持つことになる。
ゆえに、$f(x)=\Phi_n(x)$
となり、$\Phi_n(x)$が整数係数の範囲で既約であることが導かれた
(証明終了)
まとめ
おつかれさまでした!
ここまでお読みいただきありがとうございます。
大変うれしく思います。
円分多項式の既約性はガロア理論で結構重要な役割を果たしますし、
他にも数論の随所で大活躍する性質です。
ではまた次回の記事でお会いしましょう!
参考
[1] 高木貞治, 代数学講義(改訂新版), 共立出版, 1965
[2] 高木貞治, 初等整数論講義(第2版), 共立出版, 1971
画像素材提供(アイキャッチ):Gerd AltmannによるPixabayからの画像

コメント