定期試験や模試で高得点をとれたことが数学を好きになったきっかけだという人は多いのではないでしょうか。
入試は大学の先生たちが受験生の能力を計るために頭を悩ませながらようやく作り出したある種の芸術作品で、それがどんどん解けるようになる過程は間違いなく楽しいものです。
では、どのように入試問題にアプローチしていくのか。
難しい問題であっても、基礎的な知識の組み合わせであり、その問題を構成するパーツ一つ一つのレベルまで分解すれば、それほど苦戦することなく解けてしまうものです。
ここでは、どういった条件に着目してどの知識を引っ張り出して組み合わせて行けばいいのか、その思考回路をマスターするために必要なことを、授業編・基礎編・応用編に分けてまとめていきます。
問題を解くことを楽しんでいきましょう。
目次
授業編
数学Ⅰ 2次方程式の解の公式
あわせて読みたい


平方完成で求める2次方程式の解の公式
【まずはシンプルな形から】 2次方程式史上最もシンプルなものは、おそらく $x^2=4$ 型の2次方程式だと思います。 $x^2=4$より、$x=2, -2$です。 はい完了!簡単です…
三角比
あわせて読みたい


三角比をウルトラマンポーズとビッグライトで説明する
サイン、コサイン、タンジェント。 三角比とはウルトラマンポーズのことである 【三角比の定義】 $\sin \theta =\dfrac{b}{c}, \cos \theta =\dfrac{a}{c}, \tan \theta…
あわせて読みたい


正弦定理を円周角の定理を使って証明
今回は、数学Ⅰで習う正弦定理を円周角の定理を用いて証明します。 また、なぜ円周角の定理を使うのか、どうやってその発想にたどり着くか、 といった思考回路も合わせて…
あわせて読みたい

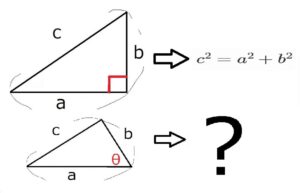
三平方の定理の拡張としての余弦定理
中学で習う三平方の定理。 あれは直角三角形についての定理でした。 これを一般の三角形の場合に拡張できないかな? というのが今回のお話。 【三平方の定理と余弦定理…
数学A ユークリッドの互除法
マスタノ!〜数学の楽しみ方〜

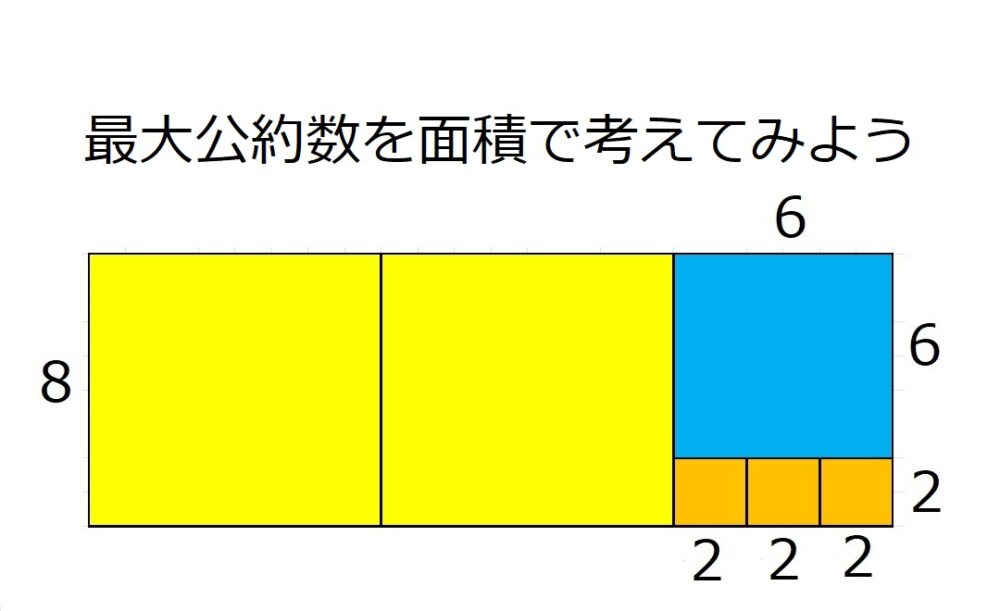
ユークリッドの互除法を面積で考える | マスタノ!〜数学の楽しみ方〜
ユークリッドの互除法って何に使うの? ユークリッドの互除法とは、2つの数の最大公約数を求めるための計算方法です。 例えば、6と8の最大公約数を考えてみましょう。 $…
あわせて読みたい


ゼロから始める1次不定方程式~丁寧さを大切に~
【1次不定方程式とは?】 $ax+by=c$の形をした方程式の整数解を求める問題を、1次不定方程式といいます。 ただし、$a, b, c$は整数です。 例えば、$3x-5y=0, 22x+5y=3…
数学Ⅱ 解と係数の関係
あわせて読みたい


解と係数の関係と基本対称式を一般化
【2次方程式の解と係数の関係】 今回は、解と係数の関係について扱っていきます。 ふつう、方程式について考えるときは、まず方程式が与えられて、それを解いて解を求…
対称式
あわせて読みたい


対称式の問題を定石と別解の2つの方法で解く
数学Ⅱの代数分野の花形といったら何を思い浮かべるでしょう? 虚数単位$i$? 多項式の割り算? 色々ありますが、僕は対称式です。 大学数学まで話を広げるとするならば、…
三角関数
あわせて読みたい


ウルトラマンと一緒に三角比を三角関数に拡張!
三角関数が待っている。 さぁ行こう! ウルトラマンポーズの向こう側へ!! 【三角比のおさらいと、三角関数の定義】 まずは三角比のおさらいから。 サインやコサインは…
基礎編
まだ工事中です
応用編
まだ工事中です