ガロア理論のアイデアを分かりやすく解説

ガロア理論は、5次方程式が代数的に解けない（べき根で解けない）ことを証明する過程で発展しました。

キーワードは、対称性。

方程式が解ける仕組みを対称性に着目して観察し、

そこから見える規則性を見つけることができたとき、

栄光はすぐそこで我々を待っています。

若きガロアがどのような発想で理論を構築していったのか。

その思考プロセスに迫っていきたいと思います。

ガロア理論とは？

ガロア理論は方程式についての理論です。

そこで、方程式について今一度考えなおしてみましょう。

例えば、

$x^2-5x+6=0$を解け

と言われたらどうしますか？

多分、多くの人は因数分解を使って解くのではないでしょうか？

$x^2-5x+6=(x-2)(x-3)$

$(x-2)(x-3)=0$

$x=2, 3$

さて。

中学校以来なにげなく使いこなしてきた因数分解ですが、

実は係数の範囲が大切です。

どういうことでしょうか？

例えば、$x^2-2$と$x^2+1$を考えてみましょう。

整数係数の範囲では、$x^2-2$　と　$x^2+1$のままです。

実数系巣の範囲では、$(x-\sqrt{2})(x+\sqrt{2})$　と　$x^2+1$です。

複素数係数の範囲では、$(x-\sqrt{2})(x+\sqrt{2})$　と　$(x-i)(x+i)$です。

このように、係数の範囲を変えると、因数分解の様子は変わっていきます。

係数の範囲を広げていくと、因数分解を進めていくことができるのです。

係数の範囲を決めたとき、もう因数分解できないと既約といい、

まだ因数分解できると可約というのでした。

ここで２次方程式について考えてみましょう。

２次方程式$ax^2+bx+c=0$には解の公式が存在します。

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

というやつです。

あえて因数分解で表すと、

$ax^2+bx+c=a(x-\dfrac{-b+\sqrt{b^2-4ac}}{2a})(x-\dfrac{-b-\sqrt{b^2-4ac}}{2a})$

です。

方程式を解くということをより数学的に考えると、

係数の世界を基の方程式の係数と根号を使って広げていって、

１次式に因数分解できる世界までたどり着けるかどうかを調べる作業と捉えることができます。

係数の世界のことを体（たい）と表現することもあります。

ちなみに、係数を広げる作業は有限回でなければいけません。

例えば、係数を複素数$\mathbb{C}$の世界まで広げると、

全ての方程式は1次式まで因数分解できますが（代数学の基本定理）、

有理数$\mathbb{Q}$から複素数$\mathbb{C}$まで数の世界を広げるにあたっては、

無限個の数を追加しなければなりませんし、

$\pi$などの根号では表せない数も追加する必要があります。

ここで、２次方程式に話を戻しましょう。

２次方程式の場合は、$ax^2+bx+c=0$

の係数$a, b, c$を有理数とすると、

係数の世界を有理数$\mathbb{Q}$から$\mathbb{Q}(\sqrt{b^2-4ac})$に広げています。

体の記号で表すと、

$\mathbb{Q} \subset \mathbb{Q}(\sqrt{b^2-4ac})$

となります。

ちなみに、

$\mathbb{Q}(\sqrt{b^2-4ac})=\lbrace x+y\sqrt{b^2-4ac} \mid x, y \in \mathbb{Q} \rbrace$

です。体（たい）の扱いや表記に馴染みのない方は、以下の記事をご覧ください。

さて、２次方程式は普通は平方完成を用いて解の公式を導出します。

$ax^2+bx+c=a(x^2+\dfrac{b}{a}x)+c$

$=a(x+\dfrac{b}{2a})^2-a(\dfrac{b}{2a})^2+c$

よって

$a(x+\dfrac{b}{2a})^2+\dfrac{-b^2+4ac}{4a}=0$

$(x+\dfrac{b}{2a})^2=\dfrac{b^2-4ac}{4a^2}$

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

となります。

３次方程式の場合は立法完成というテクニックと解と係数の関係を上手く使って

解の公式を導出します。それをカルダノの方法と言います。

４次方程式の場合も複雑さは増すもののほとんど発想は同じです。

しかし、個々の方程式を個別に解いていく方法には限界があり、

５次方程式では手も足も出ません。

それもそのはず、５次以上の方程式には解の公式が存在しないのです。

ちなみに、「解の公式が存在しない」という表現には注意が必要です。

５次以上の方程式でも、例えば$x^5-1=0$は解けます。

「解の公式が存在しない」という表現は、「解ける場合と解けない場合がある」

といった意味合いで捉えてください。

ガロア理論では、解ける方程式と解けない方程式の違いを記述できます。

要するに、方程式が解けるための必要十分条件を与えてくれるのです。

各方程式に個別のアプローチをして手詰まりなら、

新しい道具が必要。

数学の研究はいつだって

観察→規則性を発見→証明

の順番で進んできました。

これを方程式の話に落とし込むと、

各方程式を個別に解いていくのではなく、統一した物差しで解ける仕組み観察することになります。

それが対称性に着目した観察方法。

解ける方程式と解けない方程式を比べてみると、圧倒的に解ける方程式の方が少ないので、

解ける方程式（２次方程式・３次方程式・４次方程式）を観察します。

また、以下では方程式の係数は有理数でスタートすると思ってください。

これまでの記事では、ラグランジュ・リゾルベントを用いた観察結果をまとめてきましたが、

次の見出しではそれらをまとめつつ、もう一歩深い考察をしていきたいと思います。

その際、「対称式の基本定理」と「解と係数の関係」のコンボが活躍するので、

興味のある方は以下の記事をご覧ください。

２次方程式が解ける仕組みと対称性（ラグランジュ・リゾルベント）

まずはラグランジュ・リゾルベントの定義をおさらいしておきましょう。

２次方程式を

$ax^2+bx+c=0$

とし、その解を$x=x_1, x_2$とします。

この場合のラグランジュ・リゾルベントを考えましょう。

$x^2-1=0$を解くと、$x=1, -1$なので、

$1×x_1+(-1)×x_2=x_1-x_2$

です。

ここで、対称性に着目していきます。

$x_1, x_2$の２つの並べ替えは、２！＝２通りです。

具体的には、

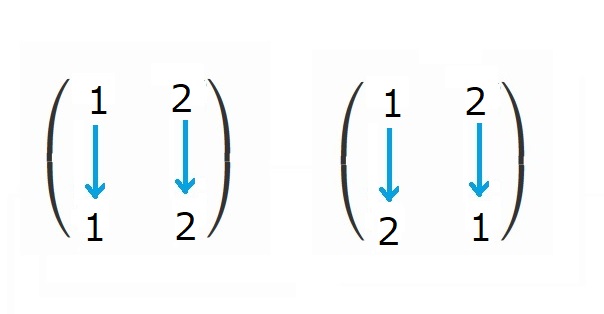
の２つです。

$x_1-x_2$

にこの２つの並び替えを作用させてみましょう。

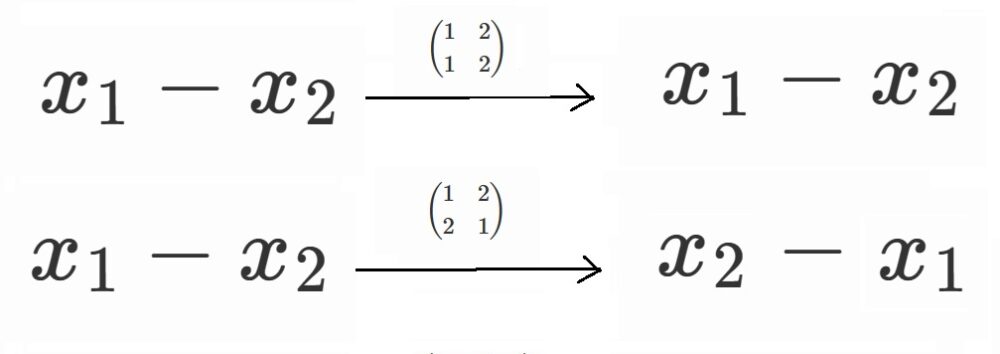
$x_1-x_2 \neq x_2-x_1$

なので、$x_1-x_2$はこの２つの並び替えで不変にならず、対称式ではありません。

しかし、２乗すると、

$(x_1-x_2)^2$

はこの２つの並び替えのどちらでも不変で、対称式となります。

対称式の基本定理より、対称式は基本対称式で表すことができます。

ここで、解と係数の関係より、

$x_1+x_2=-\dfrac{b}{a}$

$x_1x_2=\dfrac{c}{a}$

だったので、基本対称式は元の方程式の係数で表されます。

よって、

$(x_1-x_2)^2$

は元の方程式の係数で表されることになります。

実際、

$(x_1-x_2)^2=(x_1+x_2)^2-4x_1x_2$

$=(\dfrac{b}{a})^2-4\dfrac{c}{a}$

$=\dfrac{b^2-4ac}{a^2}$

したがって、

$(x_1-x_2)^2=\dfrac{b^2-4ac}{a^2}$

となり、両辺２乗根をとると、

$x_1-x_2=\pm \dfrac{\sqrt{b^2-4ac}}{a}$

です。

ここで、

$x_1+x_2=-\dfrac{b}{a}$

$x_1-x_2=\pm \dfrac{\sqrt{b^2-4ac}}{a}$

の連立方程式を解くと、

$x_1, x_2=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

となり、解の公式が導かれます。

これらのことを整理しなおしましょう。

今起こったことを、

・体の世界の話

・ラグランジュ・リゾルベントの話

・並べ替えの話

の３つの視点でまとめると、以下のようになります。

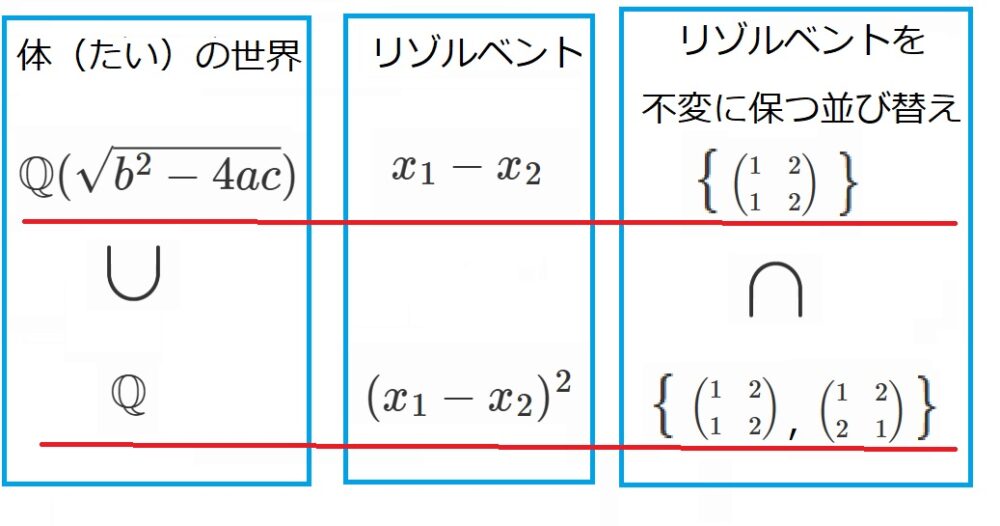
どうです？

ヤバくないですか？

なんか、体の世界と並べ替えの世界は、逆向きに対応しているっぽいですよね！！

このヤバさに目を付けたガロアの洞察力には驚嘆するばかりです。

３次方程式はより一層ヤバいですよ！

刮目せよ！！！

3次方程式が解ける仕組みと対称性（ラグランジュ・リゾルベント）

３次方程式$ax^3+bx^2+cx+d=0$の３つの解を

$x=x_1, x_2, x_3$

とします。

また、$x^3-1=0$の解を$x=1, \omega, \omega^2$

とすると、３次のラグランジュ・リゾルベントは

$x_1+\omega x_2+\omega^2 x_3$

となります。

さて、３つの解の並べ替えは全部で３！＝６通り。

具体的には以下の６つです。

$x_1+\omega x_2+\omega^2 x_3$に

これら６つの並べ替えを作用させてみましょう。

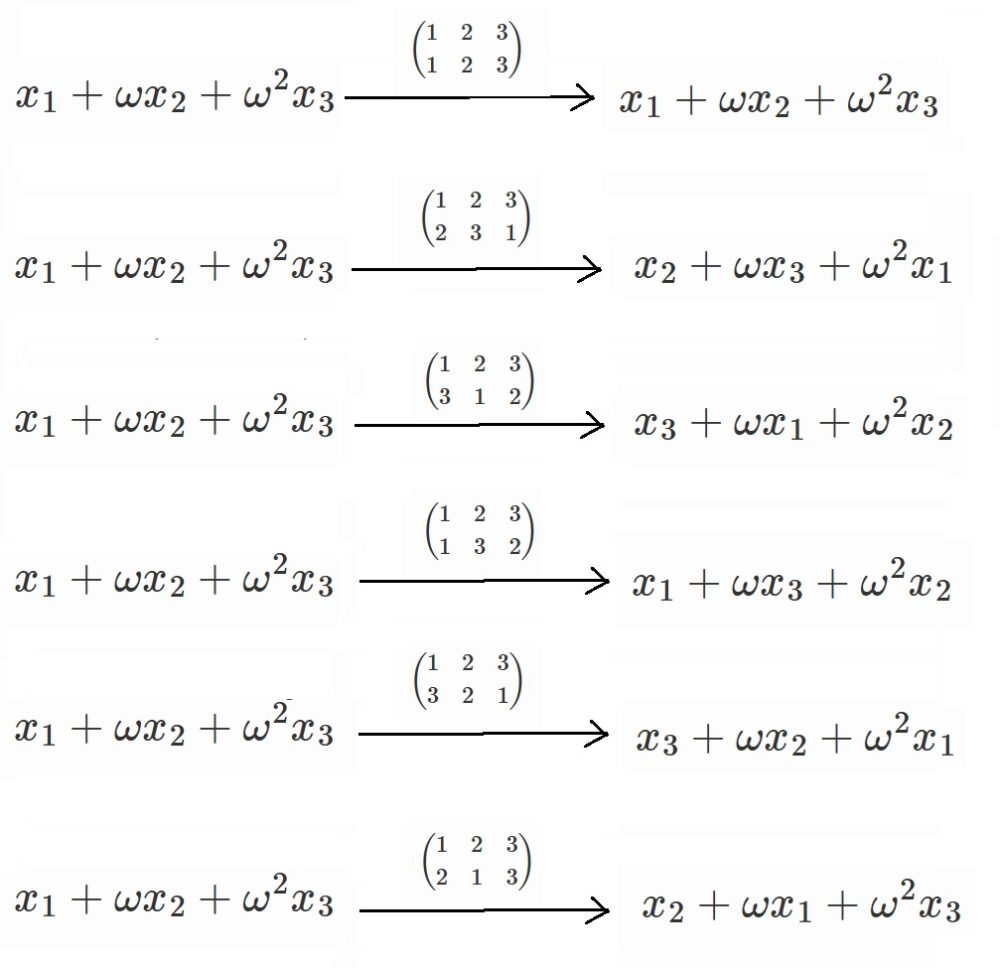
全然対称式じゃありません。

そこで、３乗して

$(x_1+\omega x_2 +\omega^2 x_3)^3$

を考えます。

同じように、これに６通りの並べ替えを作用させてみましょう。

$(x_1 +\omega x_2 +\omega^2 x_3)^3$は

対称式ではありませんが、６つの並べ替えのうち、

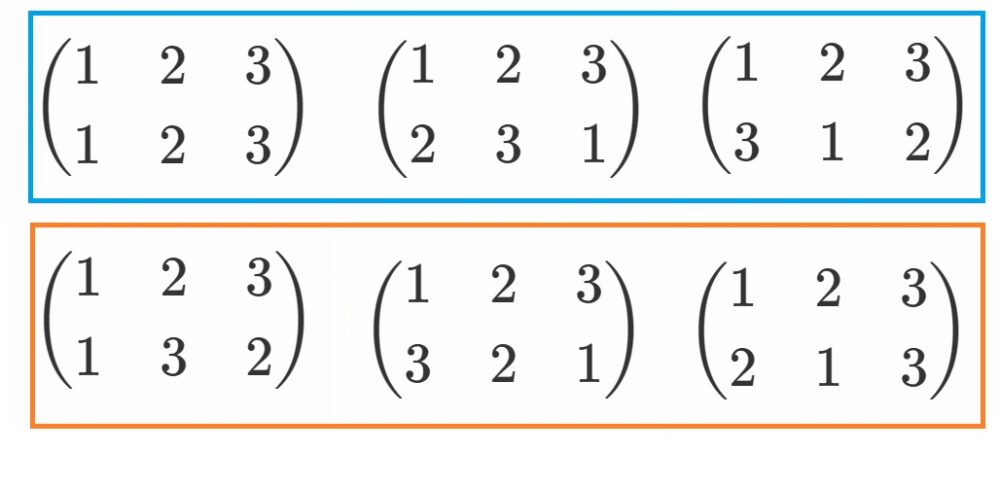
青枠でくくった並べ替えに関しては不変です。

$x_1 +\omega x_2 +\omega^2 x_3$

と比べると、格段に対称性が高くなっています。

ここで、

$S^3=(x_1 +\omega x_2 +\omega^2 x_3)^3$

$T^3=(x_1 +\omega x_3 +\omega^2 x_2)^3$

とすると、この２つについては２次方程式のリゾルベントと同じ考え方が適応できます。

すなわち、

$(S^3-T^3)^2$

が対称式となり、うまいこと２次方程式に落とし込むことで

$x_1, x_2, x_3$を求めることができるのです。

これが３次方程式が解ける仕組みです。

更に詳細な解説は以下をご覧ください。

さて、ここからです。

$(x_1 +\omega x_2 +\omega^2 x_3)^3$

を不変に保つ３つの並べ替え（青枠のやつら）に着目して観察を深めていきましょう。

こいつら、全部

$x_1$　→　$x_2$　→　$x_3$

がこの順番でグルグル回る並べ替えになってませんか？

なってますよね！！

簡略のため、ここからは並べ替えたちを文字で置くことにします。

まず、なにも並べ替えない、という並べ替えですが、これは慣例上$e$で表します。

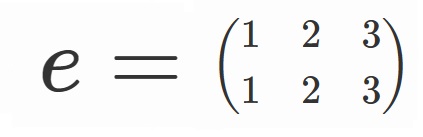
ここで、

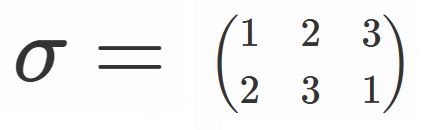
と置くことにしましょう。

また、

$x_1 +\omega x_2 + \omega^2 x_3$に$\sigma$を作用させることを

$\sigma (x_1+\omega x_2+\omega^2 x_3)$

とかくことにします。

すると、

$\sigma (x_1+\omega x_2+\omega^2 x_3)=x_2+\omega x_3 +\omega^2 x_1$

です。これはまぁ、ほぼ当たり前です。並べ替えの定義ですから。

ヤバいのはここからです。

$x_2+\omega x_3 +\omega^2 x_1$

に更にもう一回$\sigma$を作用させてみます。

$\sigma (x_2+\omega x_3+\omega^2 x_1)=x_3+\omega x_1 +\omega^2 x_2$

要するに、

$x_1 + \omega x_2 +\omega^2 x_3$に

$\sigma$を２回作用させると

$x_3+\omega x_1 +\omega^2 x_2$になるということで、

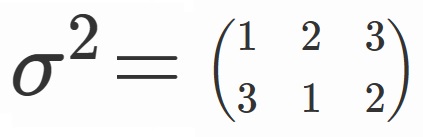
ということです。

これらのことから、

$(x_1 +\omega x_2 +\omega^2 x_3)^3$を不変に保つ３つの並べ替えは、

$\lbrace e, \sigma, \sigma^2 \rbrace$

と表されることが分かります。（ちなみに、$\sigma^3=e$です。）

ついでなので、オレンジ枠の奴らについても軽く考察しておきましょう。

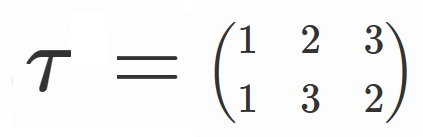
と置くことにします。

オレンジの枠の奴らは、

$x_1$　→　$x_3$　→　$x_2$

の順番でグルグル回っているので、

$\lbrace \tau, \tau \sigma, \tau \sigma^2 \rbrace$

となります。

すると、３！＝６並べ替えたちは、

$\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$

という集合で表されることになります。

３つの並べ替え全体の集合には、３次の置換群という名前がついており、

これを$S_3$で表す慣例です。

置換群という言葉の定義は今回の記事では扱いません。

あ、そんな名前がついてるんだな、くらいの認識でOKです。

$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$

ということです。

ちなみに、$(x_1+\omega x_2 +\omega^2 x_3)^3$を

不変に保つ並べ替えたち（青枠の並べ替えたち）にも名前がついていて、

これは３次の交代群といいいます。$A_3$で表す慣例です。

$A_3=\lbrace e, \sigma, \sigma^2 \rbrace$

さて。

２次方程式の場合と同じように、ここまでのことを

・体の世界の話

・ラグランジュ・リゾルベントの話

・並べ替えの話

の３点で整理しましょう。

どうですか？

とてつもなくヤバい何かの片鱗を見た気になりませんか？

ひとまず、体の世界と並べ替えの世界は、ここでも逆向きに対応しています！

そして！

緑の文字が何やら気になります。

まずは体の世界の緑の文字について説明します。

$\mathbb{Q}(\omega ) \subset K_0(\sqrt{(S^3-T^2)^2})$

のところの２乗根という文字です。

これはシンプルで、$\sqrt{(S^3-T^3)^2}$という２乗根の数を追加したよ！という意味です。

体拡大の言葉を知っている方なら、拡大次数が２と読み替えてもよいです。

次の$K_0(\sqrt{(S^3-T^2)^2}) \subset K_1(S)$

もほぼ同じです。$S^3$の３乗根を取って$S$を追加しているので、３乗根とかいています。

これも体の拡大次数が３と読み替えることができます。

体拡大については、今後の記事で解説していきますので、ご期待ください。

体の世界話はひとまずここまで。

問題は、並べ替えの世界の６÷３とか、３÷１です。

まずは

$\lbrace e, \sigma, \sigma^2 \rbrace \subset \lbrace e, \sigma, \sigma^2, \tau, \tau\sigma, \tau\sigma^2 \rbrace$

の横の６÷３に着目しましょう。

$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau\sigma, \tau\sigma^2 \rbrace$

の元の数が６個で、

$A_3=\lbrace e, \sigma, \sigma^2 \rbrace $

の元の数が３個なので、

６÷３＝２とかいているわけなのですが、

それ以上の意味合いがあります。

$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau\sigma, \tau\sigma^2 \rbrace$

を、$\tau$がいない前半部分と、$\tau$がいる後半部分で分けて眺めてください。

ちょっと強引ですけど、

（後半部分）$=\tau \lbrace e, \sigma, \sigma^2 \rbrace=\tau A_3$

です。要するに、

$S_3=A_3 \cup \tau A_3$

となっています。

$S_3$は$A_3$と$\tau$によって、元の数が３個ずつの２つの集合に分けることができるのです！

$\lbrace A_3, \tau A_3 \rbrace$

という集合を考えましょう。

これは$S_4$を$A_3$と$\tau$によって前半と後半に分けてできた集合です。

あたかも$S_3$を$A_3$で割り算しているかのように見えるので、

これを

$S_4 /A_3=\lbrace A_3, \tau A_3 \rbrace$

のように表すことがあります（剰余群といいます）

緑の文字の６÷３＝２は、

剰余群$S_4 /A_3$の元の数が２個であることを表していたのです！！

しかも！

これが体の世界の２乗根の２と対応しているのですから驚きです！！

さらには、$S_4 /A_3=\lbrace A_3, \tau A_3 \rbrace$は群という構造を持ちます！！

（群という概念は次回の記事で詳しく解説しようと思いますので、今はふーんでOKです）

３÷１＝３については、

$e \lbrace e, \sigma, \sigma^2 \rbrace=\lbrace e, \sigma, \sigma^2, \rbrace$

なので、$A_3 / \lbrace e \rbrace =A_3$であることが対応しています。

お次は４次方程式です！！

4次方程式が解ける仕組みと対称性（ラグランジュ・リゾルベント）

４次方程式$ax^4+bx^3+cx^2+dx+e=0$

の４つの解を$x=x_1, x_2, x_3, x_4$

とします。また、

$x^4-1=0$の解を$x=1, \zeta_4, \zeta_4^2, \zeta_4^3$とします。

（実際には$\zeta_4=i$ですが）

すると、４次のラグランジュ・リゾルベントは

$x_1+\zeta_4x_2+\zeta_4^2x_3+\zeta_4^3x_4$

となります。

一方、４つの解の並べ替えは４！＝２４通りあります。

３次方程式の場合と比べると圧倒的に多いですね笑

一応書き下しておくと、以下のようになります。

これら２４こ全部をひっくるめて集合を作ると、

4次の置換群という名前が付き、$S_4$で表されます。

ここで、

$L_1=x_1+\zeta_4x_2+\zeta_4^2 x_3+\zeta_4^3 x_4$

と置くことにし、２４通りの並び替えを作用させたものを順に

$L_1, L_2, \cdots, L_{24}$としましょう。

全て書き下すと次のようになります

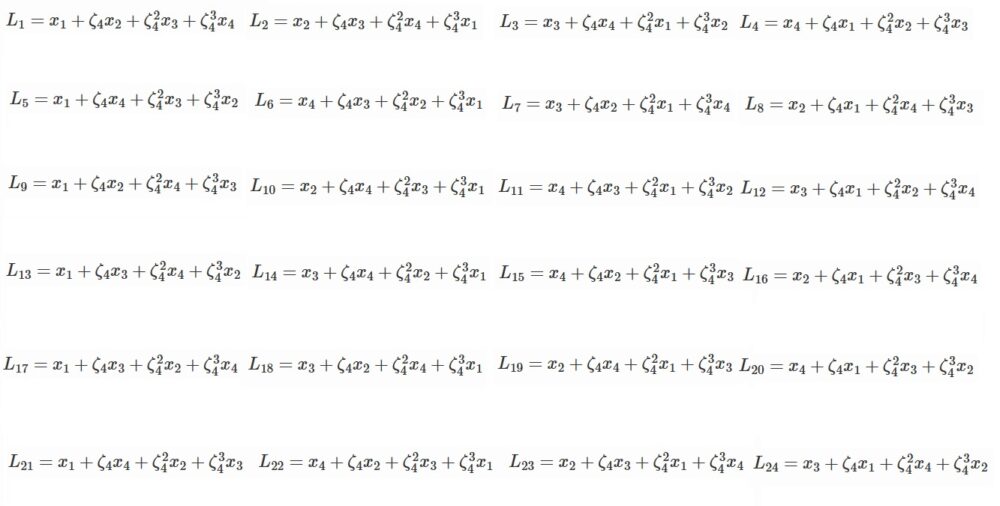
さて、４次方程式の場合は４が素数ではないためにもともと少しだけ対称性が高い状態であり、

$L_1$をいきなり４乗はしないのでした。

$\zeta_4=i$に注意すると、

$L_1=(x_1-x_3)+(x_2-x_4)i$

です。一方、

$L_5=(x_1-x_3)-(x_2-x_4)i$

です。

$(L_1)^2+(L_5)^2=2(x_1-x_3)^2-2(x_2-x_4)^2$

です。

同じように隣の$(L_2)^2+(L_6)^2$を考えると、

$(L_2)^2+(L_6)^2=2(x_2-x_4)^2-2(x_1-x_3)^2$

であり、

$(L_2)^2+(L_6)^2=-\lbrace (L_1)^2+(L_5)^2 \rbrace$

に気づきます。

よって、

$\lbrace (L_1)^2+(L_5)^2 \rbrace^2=\lbrace (L_2)^2+(L_6)^2 \rbrace^2$

が成立します。

となります。横にスライドしつつ同じ作業を繰り返していくと、

$\lbrace (L_1)^2+(L_5)^2 \rbrace^2=\lbrace (L_2)^2+(L_6)^2 \rbrace^2=\lbrace (L_3)^2+(L_7)^2 \rbrace^2=\lbrace (L_4)^2+(L_8)^2 \rbrace^2$

同様のことを下に並んでいる奴らについても繰り返していくと、

$\lbrace (L_9)^2+(L_{13})^2 \rbrace^2=\lbrace (L_{10})^2+(L_{14})^2 \rbrace^2=\lbrace (L_{11})^2+(L_{15})^2 \rbrace^2=\lbrace (L_{12})^2+(L_{16})^2 \rbrace^2$

と

$\lbrace (L_{17})^2+(L_{21})^2 \rbrace^2=\lbrace (L_{18})^2+(L_{22})^2 \rbrace^2=\lbrace (L_{19})^2+(L_{23})^2 \rbrace^2=\lbrace (L_{20})^2+(L_{24})^2 \rbrace^2$

が成り立ちます。

ここで、

$\lbrace (L_1)^2+(L_5)^2 \rbrace^2=A$

$\lbrace (L_9)^2+(L_{13})^2 \rbrace^2=B$

$\lbrace (L_{17})^2+(L_{21})^2 \rbrace^2=C$

と新たに置き、

$A, B, C$を用いて３次のラグランジュ・リゾルベントを新たに作って３乗して

$S^3=(A+\omega B+\omega^2 C)^3$

$T^3=(A+\omega C+\omega^2 B)^3$

とすると、

$(S^3-T^3)^2$が対称式となります。

より詳細な解説は以下の記事をご覧ください

ここまでのことを体で表すと、

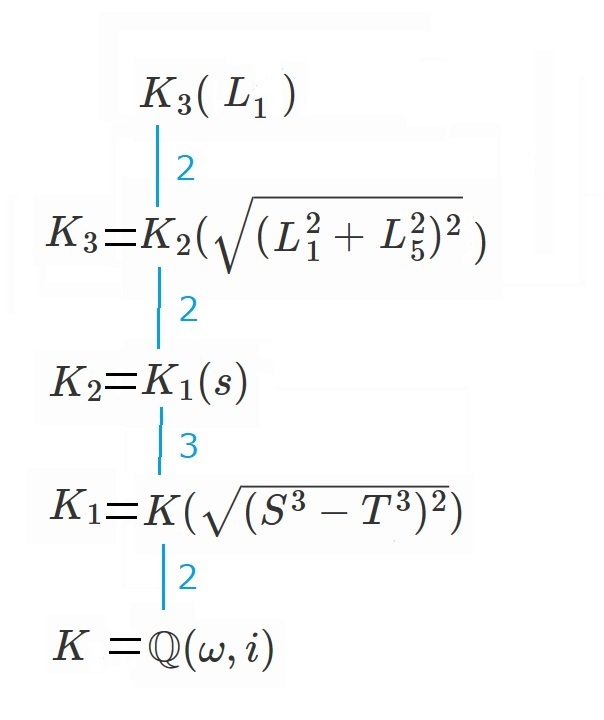
さて、ここからはラグランジュ・リゾルベントの話を見ていきましょう。

まずは$S^3-T^3$を不変に保つ並べ替えを調べます。

頑張ると、紫色で囲まれた以下の１２個と分かります（さらっと書いていますが、実際は結構大変でした）

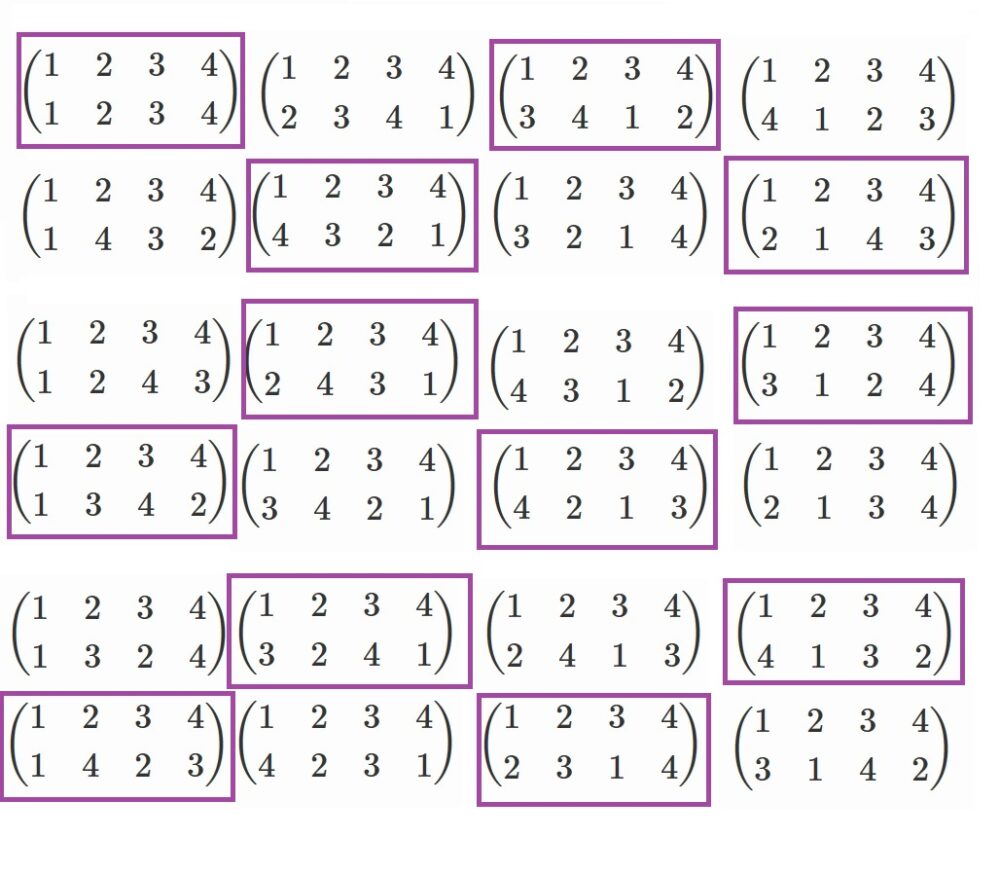
この紫の奴らが４次の場合の交代群に当たり、$A_4$です。

（交代群についてはまた別の記事で取り上げます。今は雰囲気だけ感じてください）

次に$S=A+\omega B+\omega^2 C$

を不変に保つ奴らを見ていきましょう。

これは、

青枠の奴らとなります。（これも調べるのは結構大変でした）

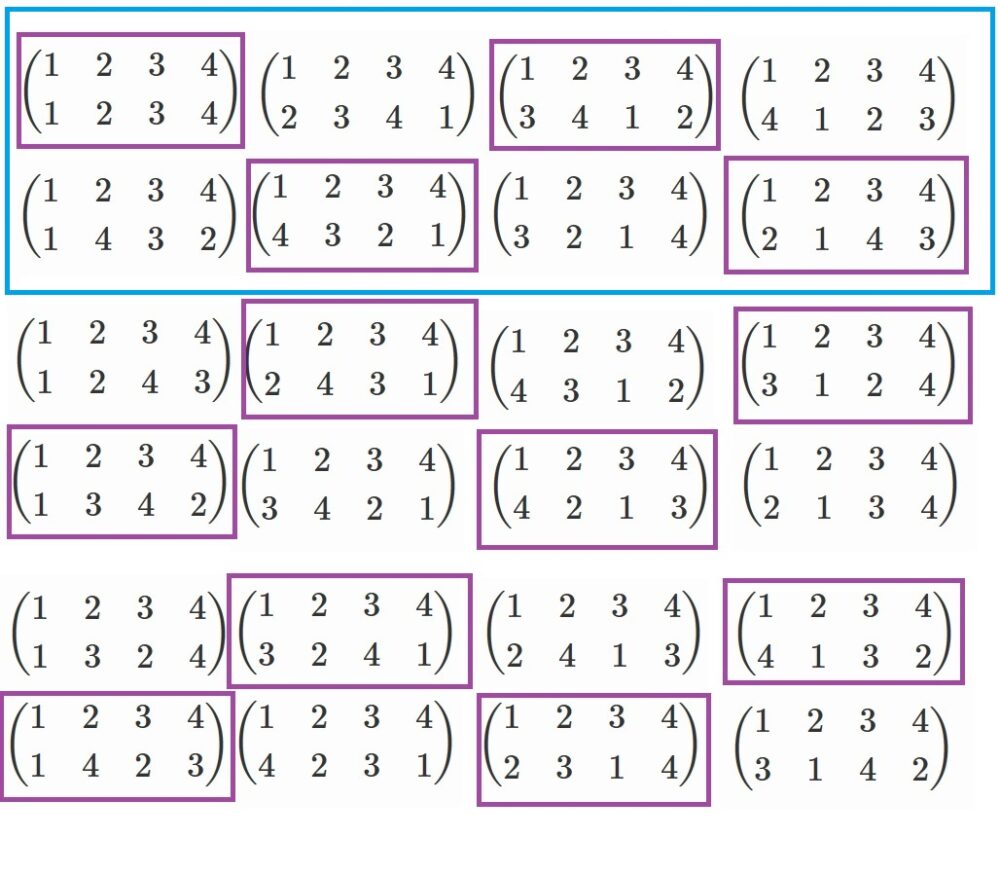
ここで、紫で囲まれた奴らのうち、青枠でもある奴らで構成される集合を

クラインの4元群といい、慣例で$V$と表します。

簡略のため、

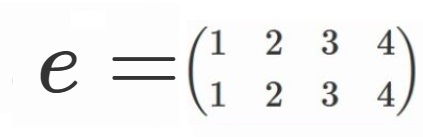
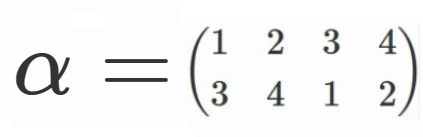
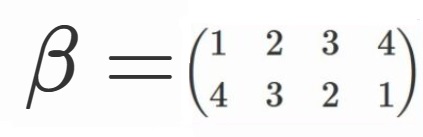
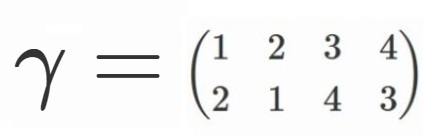
と定めることにしましょう。

$V=\lbrace e, \alpha, \beta, \gamma \rbrace$

です。

そして$V$の元のうち、

$(L_1)^2+(L_5)^2$を不変に保つ奴らは、

$e$　と　$\alpha$　です。

要するに$\lbrace e, \alpha \rbrace$です。

ここまでのことを整理すると、以下のようになります。

集合（群）の割り算については、

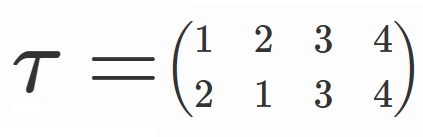
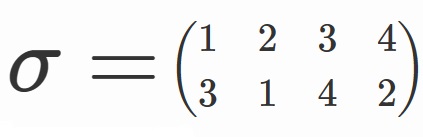
を使うと見通しがよくなります。

$S_4/A_4=\lbrace A_4, \tau A_4 \rbrace$

$A_4/V=\lbrace V, \sigma V, \sigma^2 V \rbrace $

$V/\lbrace e, \alpha \rbrace = \lbrace \lbrace e, \alpha \rbrace, \beta \lbrace e, \alpha \rbrace \rbrace $

$\lbrace e, \alpha \rbrace / \lbrace e \rbrace = \lbrace e, \alpha \rbrace $

です。

4次方程式の場合も、体の世界と並べ替えの世界は逆向きに対応しています。

また、集合（群）の割り算に着目すると、

$S_4/A_4$　の元の数は２

$A_4/V$　の元の数は３

$V/\lbrace e, \alpha \rbrace $　の元の数は２

$\lbrace e, \alpha \rbrace / \lbrace e \rbrace $　の元の数は２

$2, 3, 2, 2$

は全て素数です。

素数が重要っぽい役割を演じていると、なんかそれだけで少し嬉しい気分ですね！

思えば、３次方程式の場合、２次方程式の場合も集合（群）の割り算で発生する集合（群）の元の数は素数でした。

まとめ

数学の研究は、観察→規則性を発見→証明のステップで発展していきます。

今回の記事では、2次方程式、3次方程式、4次方程式を対称性に基づいて観察しました。

その結果、みつけた規則性はつぎの2つです

①　体の世界と並べ替えの世界は逆向きに一対一対応している

②　並べ替えの世界に着目すると、集合（群）の割り算でできる集合（剰余群）の元の個数は必ず素数

①こそがガロアの発見した偉大な定理であり、彼への敬意をこめてガロア理論の基本定理と呼ばれています。

また、②の規則性こそが、実は方程式が解けるための必要十分条件です。

今回の記事では、あくまでも観察と規則性の発見まで

証明のためにはいろいろ道具をそろえる必要があります。

次回の記事では「群」という道具をゲットし、群論をスタートさせようと思います

ご期待ください。

次の記事

参考

画像素材提供（アイキャッチ）：JoeによるPixabayからの画像