群の同型写像と準同型写像を具体例で分かりやすく

群論を進めていくと、いずれは同型写像や準同型写像と出会います。

今回は、同型写像や準同型写像の条件がなぜあのような形になっているのか、

その意味と意義について考えていきたいと思います。

同型写像の本質は、ある群と別の群がどのくらい似ているか調べるもの、と捉えると分かりやすいです。

そこで、具体例を通して群の同型写像と準同型写像を解説していきます。

群の同型写像の具体例を確認

初めに同型写像の定義を述べておきます。

今回の記事では、

$f(a*b)=f(a)〇f(b)$

という条件が何なのか、なぜこんなものを考えると嬉しいのか、

という点を考察していきたいと思います。

この条件は普通は$*$や$〇$は省略して

$f(ab)=f(a)f(b)$と表します。

大半の数学書では上記の表し方で記述されているはずです。

しかし、今回は$*$と$〇$は別の演算でもよいという点を強調しておきたいので、

あえて省略せずに

$f(a*b)=f(a)〇f(b)$

と表していますので、混乱のないよう注意してください。

同型写像を考えるうえでは、

ある群と別の群を見比べて似ているかどうか考える、

という発想がとても大切です。

「同型」という言葉は、「似ている」「同じ構造をもっている」

といった感覚でイメージすると分かりやすいです。

ここでは４つの群を例として取り上げようと思います。

１の６乗根、３次の対称群、１の６乗根の部分群、３次の対称群の部分群

の４つです。

１の６乗根を集めた群を$G_1$とします。

$G_1=\lbrace \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5, 1 \rbrace$

です。

$\zeta_6$は１の６乗根なので、$\zeta_6^6=1$となります。

また、$G_1$の部分群$H_1$を次のように定義しようと思います。

$H_1=\lbrace 1, \zeta_6^2, \zeta_6^4 \rbrace$

次に３次の置換群を考えます。

３次の対称群は$S_3$で表すのが慣例です。

３個の並べ替えは３！＝６通りで、具体的には以下の６つです。

ここで、

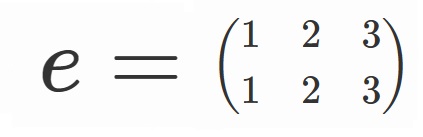
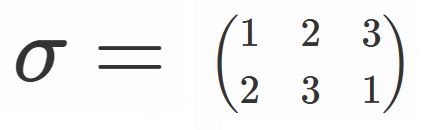
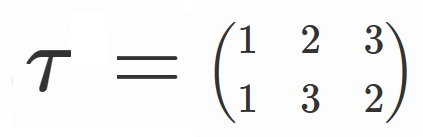
と表すことにすると、

$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$

となります。

また、$A_3=\lbrace e, \sigma, \sigma^2 \rbrace$

とします。

さて。

これらが似ているかどうか調べていきましょう。

その際に手掛かりとなるのは、演算表です。

$G_1$　と　$S_3$　の演算表はそれぞれ次のようになります。

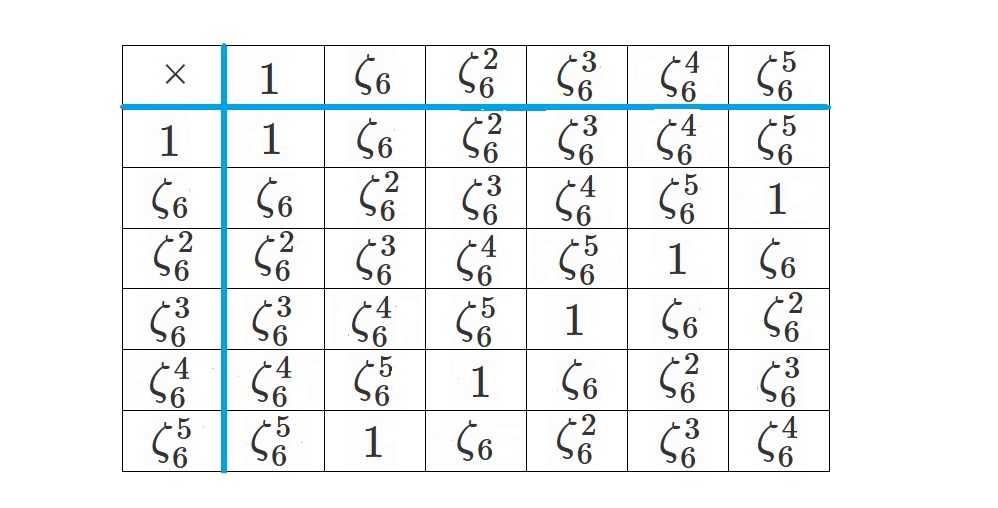
そして、$H_1$　と　$A_3$　の演算表はそれぞれ次です。

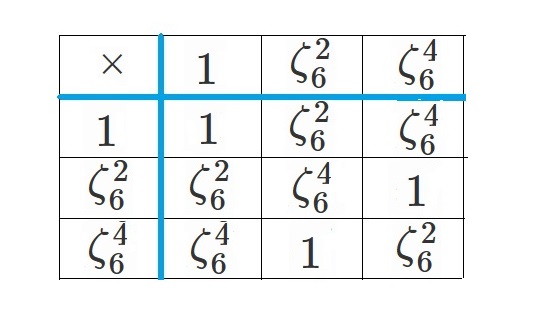
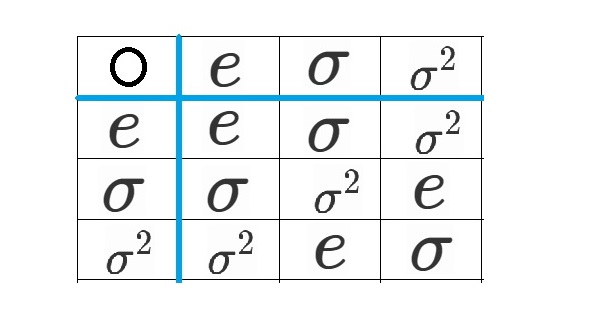
どうですか？

「$G_1$　と　$S_3$　のペア」

と

「$H_1$　と　$A_3$　のペア」

どちらのペアの方が似ているでしょうか？？

「似ている」という言葉はとても曖昧で、はっきりした定義があるわけでもありませんが、

直観的には、「$H_1$　と　$A_3$　のペア」の方が似ている、

と感じた方が多いのではないかと思います。

なぜか？

それは、演算表に対応関係があるからです。

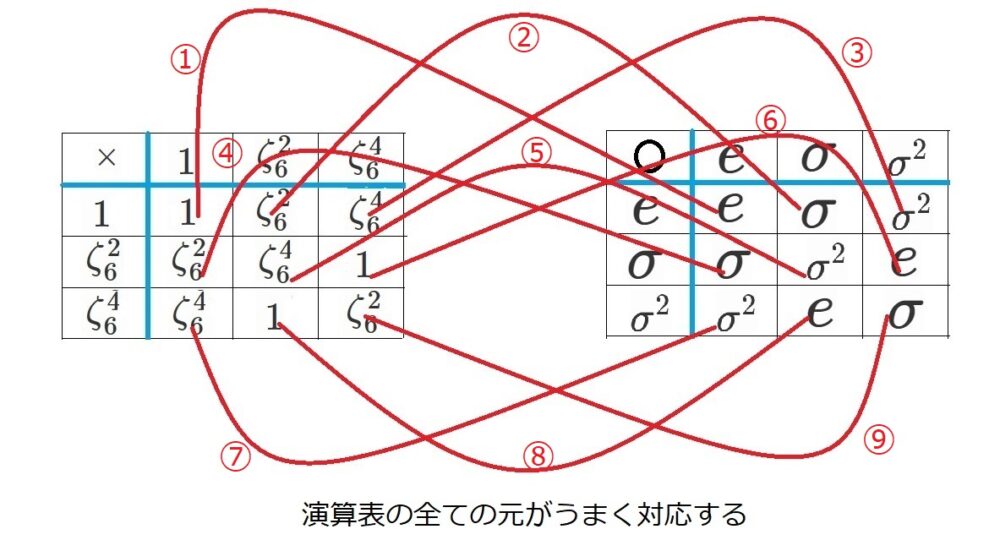
これをもう少し丁寧に考えていきましょう。

$H_1$　と　$A_3$　の対応付けを　$f$　とします。

演算表を考える前に、

まず$H_1$と$A_3$の元それぞれに対応付けをしておかなければならないので、

$f(1)=e$

$f(\zeta_6^2)=\sigma$

$f(\zeta_6^4)=\sigma^2$

としておきます。

次に演算表の対応を考えていきましょう。

①　$f(1×1)=e 〇 e$

②　$f(1×\zeta_6^2)=e〇 \sigma$

③　$f(1×\zeta_6^4)=e〇 \sigma^2$

④　$f(\zeta_6^2 ×1)=\sigma 〇 e$

⑤　$f(\zeta_6^2 × \zeta_6^2)=\sigma 〇 \sigma$

⑥　$f(\zeta_6^2 × \zeta_6^4)=\sigma 〇 \sigma^2$

⑦　$f(\zeta_6^4 × 1)=\sigma^2 〇 e$

⑧　$f(\zeta_6^4 × \zeta_6^2)=\sigma^2 〇 \sigma$

⑨　$f(\zeta_6^4 × \zeta_6^4)=\sigma^2 〇 \sigma^2$

こうですね。

ここで、例えば②に着目しましょう。

②　$f(1×\zeta_6^2)=e〇 \sigma$

ここで、$f(1)=e$　と　$f(\zeta_6^2)=\sigma$　を②に代入しましょう。

$f(1 × \zeta_6^2)=f(1)〇f(\zeta_6^2)$

が成り立っています。

他の場合も同じ式が成り立つことが確認されます。

要するに、

$a, b \in H_1$について、

必ず$f(a×b)=f(a)〇f(b)$

が成り立ちます。

この式こそが、「同型」という概念をつかさどる条件です！

「同型」のイメージは、「似ている」「同じ構造をもっている」です。

そして、ある群と、別の群が「似ている」かどうかは、

$f(ab)=f(a)f(b)$

を満たす写像が作れるかどうかで判断できるのです！！！

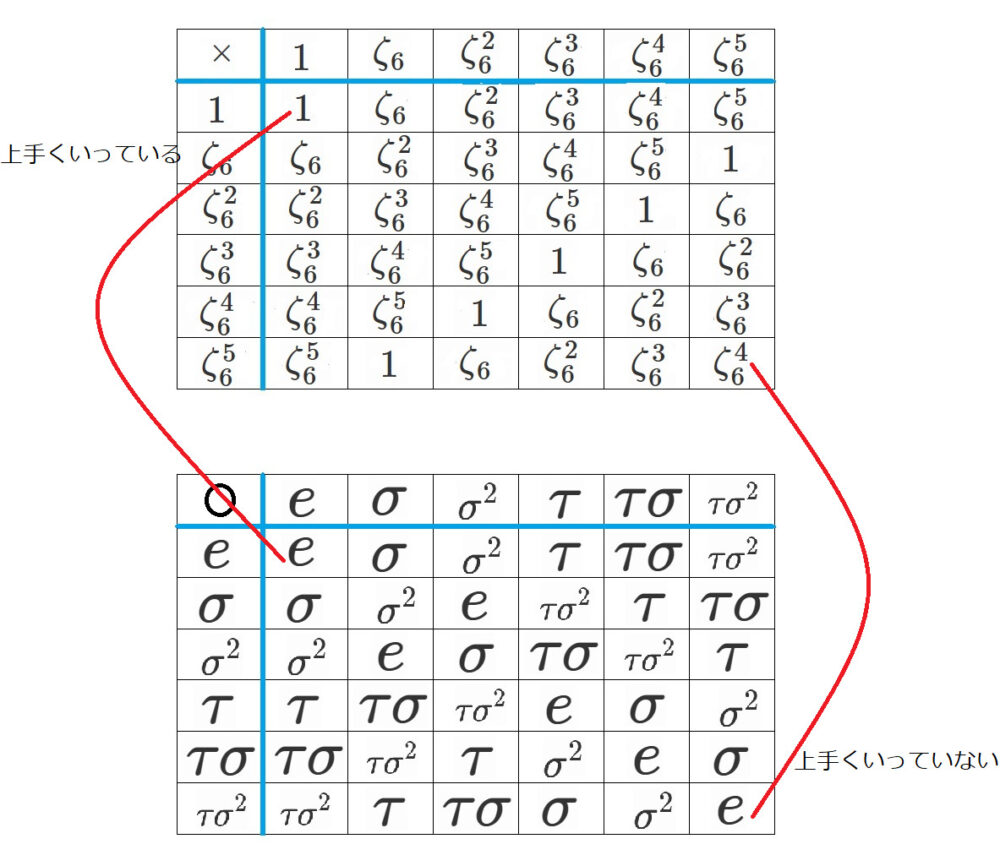
$G_1$　と　$S_3$　の場合ではこの性質を満たす写像をうまく作れません。

そのことを確かめておきましょう。

$G_1$　と　$S_3$　の対応付けを　$g$　とします。

$G_1$と$S_3$の元それぞれに対応付けを

$g(1)=e$

$g(\zeta_6)=\sigma$

$g(\zeta_6^2)=\sigma^2$

$g(\zeta_6^3)=\tau$

$g(\zeta_6^4)=\tau \sigma$

$g(\zeta_6^5)=\tau \sigma^2$

とします。

ここで、演算表を参考にすると、例えば

$g(1×1)=e〇e$

で、$g(1)=e$を代入すると

$g(1×1)=g(1)〇g(1)$

が成り立ちます。

ここで、$g(\zeta_6^5 × \zeta_6^5)=\tau \sigma^2 〇 \tau \sigma^2$

はどうでしょうか？

$g(\zeta_6^5)=\tau \sigma^2$

なので、

$g(\zeta_6^5 × \zeta_6^5)=\tau \sigma^2 〇 \tau \sigma^2$

に代入すると、

$g(\zeta_6^5 × \zeta_6^5)=g(\zeta_6^5)〇g(\zeta_6^5)$

は一見すると成り立っていそうな気もします。

しかし、ちょっと立ち止まって考えてみましょう。

$\zeta_6^5 × \zeta_6^5=\zeta_6^4$でした。

よって、

$g(\zeta_6^5 × \zeta_6^5)=g(\zeta_6^4)$

です。

ここで、

$g(\zeta_6^4)=\tau \sigma$

でしたので、

$g(\zeta_6^5 × \zeta_6^5)=g(\zeta_6^4)=\tau \sigma$

です。

しかし、

$g(\zeta_6^5 × \zeta_6^5)=\tau \sigma^2 〇 \tau \sigma^2$

について、演算表より$\tau \sigma^2 〇 \tau \sigma^2=e$でなければなりません。

ゆえに$g(\zeta_6^5 × \zeta_6^5)=e$でなければなりません。

$g(\zeta_6^5　× \zeta_6^5)=\tau \sigma$

と

$g(\zeta_6^5 × \zeta_6^5)=e$

が同時に成り立たないといけないことになりますが、

これではwell-definedとは言えないので、

$g$は写像になりえません。

同型写像の定義

ここで、あたらめて定義を確認しておこうと思います。

同型写像が作れるときは、$G_1$と$G_2$は同じ構造をもつそっくりさんと捉えることができます。

ちなみに、同型写像から「全単射」という条件を緩めたものは準同型写像といいます。

群の同型写像の例

例①

まずは先ほどの

$H_1=\lbrace 1, \zeta_6^2, \zeta_6^4 \rbrace$

と

$A_3 =\lbrace e, \sigma, \sigma^2 \rbrace$

を考えましょう。

これは、

$H_1$から$A_3$への写像として、$f$を

$f(\zeta_6^a)=\sigma^{\frac{a}{2}}$　$(a=2, 4, 6)$

とすると上手くいくのでした。

実際、$a, b \in H_1$のとき、

$f(\zeta_6^a ×\zeta_6^b)=f(\zeta_6^a)〇f(\zeta_6^b)$

となるのは、先ほどの見出しで確認した通りです。

よって$H_1 \cong A_3$

です。

例②

$\mathbb{Z}/4\mathbb{Z}=\lbrace \bar{1}, \bar{2}, \bar{3}, \bar{0} \rbrace$

は加法について群となります。

また、$G=\lbrace i, i^2, i^3, i^4 \rbrace$

とします。$i^2=-1$なので、

実質的には$G=\lbrace i, -1, -i, 1 \rbrace$

となります。

$G$は乗法について群となります。

ここで、$\mathbb{Z}/4\mathbb{Z}$から$G$への写像$f$を

$f(\bar{n})=i^{n}$と定めましょう。

すると、$\bar{m}, \bar{n} \in \mathbb{Z}/4\mathbb{Z}$に対して

$f(\bar{m}+\bar{n})=i^{m+n}$

$=i^{m}×i^{n}$

$=f(\bar{m})×f(\bar{n})$

となります。

$f(\bar{m}+\bar{n})=f(\bar{m})×f(\bar{n})$

が成り立つので、これは同型写像となり、

$\mathbb{Z}/4\mathbb{Z} \cong G$

となります。

群の準同型写像の例

例①

整数$\mathbb{Z}$は足し算について群となります。

また、$G$を演算〇についての群としましょう。

整数$\mathbb{Z}$から$G$への写像$f$を次のようにとります。

$f(n)=g^n$　$(n \in \mathbb{Z}, g \in G)$

すると、$n, m \in \mathbb{Z}$について

$f(n+m)=g^{n+m}$

$=g^n〇g^m$

$=f(n)〇f(m)$

となり、

$f(n+m)=f(n)〇f(m)$

が示されます。

よって$f$は準同型写像です。

（$f$は全単射ではないので同型写像ではないです）

例②

実数$\mathbb{R}$から０を除いた集合を$\mathbb{R}^{×}$と表すことにします。

$\mathbb{R}^{×}$は掛け算について群となります。

ここで、正の実数全体の集合を$X$とします。

$X=\lbrace x \mid x\in \mathbb{R}^{×}, x>0\rbrace$

です。

$X$もまた掛け算について群です。

ここで、$\mathbb{R}^{×}$から$X$への写像$f$を次のように定めます。

$x \in \mathbb{R}^{×}$とします。

$f(x)=\mid x \mid $　←絶対値です。

すると、$a, b \in \mathbb{R}^{×}$に対して

$f(a×b)=\mid a×b \mid$

$=\mid a \mid × \mid b \mid $

$=f(a)×f(b)$

となり、$f(a×b)=f(a)×f(b)$

となるので、これは準同型写像です。

（$f$は全単射ではないので同型写像ではありません）

準同型写像の性質

準同型写像にはひとまず覚えておきたい性質が２つあります。

（本当はもっといろいろありますが、取り急ぎは２つです。）

それを確認していこうと思います。

単位元についての性質

準同型写像によって単位元は単位元に移るよ、という内容です。

何から手を付ければよいかさっぱりなので、まずは

証明に当たって使用可能な条件式を確認していきましょう。

今回の証明の材料は、大きく３つです。

一つ目は、単位元の定義である

$ex=xe=x$　($x は群の任意の元$)

という式。

二つ目は、準同型写像の定義式

$f(a*b)=f(a)〇f(b)$

最後は$A$と$B$は群であるという条件です。

では証明をしていきます。

逆元についての性質

今回の証明もどこから進めればよいのやら分かりませんので、

前提条件から手掛かりを探っていきましょう。

今回の主役は逆元ですので、逆元の定義をおさらいしておきましょう。

$x$　が　$\alpha$　の逆元であるとは、

$\alpha x =x\alpha =e$

が成り立つことを意味するのでした。

また、結局何が証明したいの？ということをつかんでおくことも大切です。

今回示したい式

$f(a^{-1})=f(a)^{-1}$

の意味を考えましょう。

この式は、

$f(a^{-1})$が$f(a)$の逆元だよ！

と述べています。

今回は、これを手掛かりに証明を進めていきましょう。

要するに、

$\alpha x =x\alpha =e$

において、

$x$を$f(a^{-1})$に、$\alpha$を$f(a)$に置き換えて考えればよいのです。

では、証明に進んでいきましょう。

まとめ

いかがでしたか？

・ある群と別の群が似ているかどうか調べたい

・似ている群の場合は演算表にうまい対応関係がある

・どんな対応が成り立つか深めていくと、必然的に$f(ab)=f(a)f(b)$

　という条件にたどり着く

・$f$が全単射のとき、同型と呼ぶことにしよう！

といった流れを押さえていただければと思います。

また、準同型写像の性質として、

・単位元は単位元に移る

・逆元を飛ばすと、飛ばしたものの逆元になる

という単位元と逆元についての性質もぜひ押さえておいてください。

ではまた次回の記事でお会いしましょう！

参考

画像素材提供（アイキャッチ）：Gerd AltmannによるPixabayからの画像