サッカーゴールと数学
六角形のすごさを楽しんでいく企画、その②はサッカーゴールです!
みなさん、サッカーは好きですか?
一つのボールをめぐる駆け引き、1対1の躍動、そしてシュートが決まった爽快感。
多くの人を熱狂させる魔力がこのスポーツにはあります。
ちなみに僕はサッカーボールとサッカーゴールが好きです!
さて、そんなサッカーを数学の図形が陰から支えていると知ったら驚くでしょうか?
サッカーゴールのネット、一昔前は四角形のものが多かったですが、
最近テレビで見るものは大半が正六角形になっています。
これはなぜでしょう?
その理由を、
① 図形の敷き詰め
② ネットの伸縮性
という2つの観点から説明していきたいと思います。
敷き詰めができる正多角形についての説明
サッカーゴールのネットはなぜ正六角形なのか。
この謎を解き明かすには、敷き詰めというものを考えなければなりません。
まず、ネットについて考えていきます。
ネットは「同じ形のものを敷き詰めたもの」として捉えます。
実際はそういうわけでもありませんが、数学的に考えるために単純化しましょう。
また、バランスの良い形がよいので、敷き詰めるのは正多角形としましょう。
そう考えると、敷き詰めができる正多角形ってどんな図形なの?ということが問題になります。
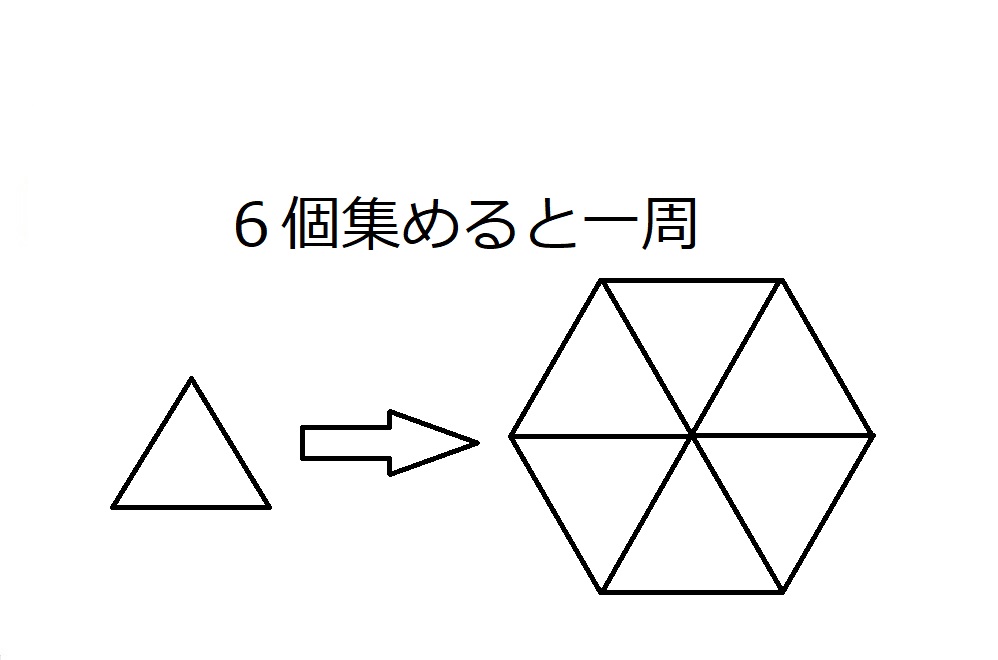
正三角形から順番に考えていきましょう。
正三角形の1つの内角の大きさは60度です。
60は360の約数。
$360=60×6$
なので、三角形6個でちょうど一周で、平面を敷き詰めることができます。
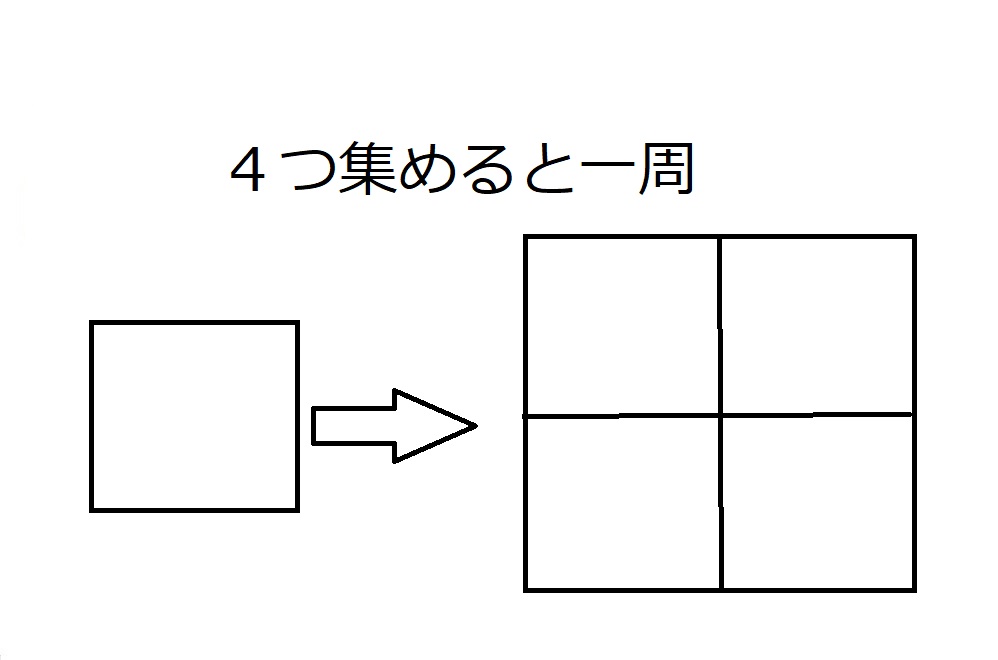
次に正方形を考えましょう。
正方形の1つの内角の大きさは90度です。
90も360の約数。
$360=90×4$
なので、正方形4つでちょうど1周で、平面を敷き詰めることができます。
次に正五角形はどうでしょうか?
正五角形の1つの内角の大きさは108度です。
108は360の約数ではないので、正五角形は敷き詰めに適しません。
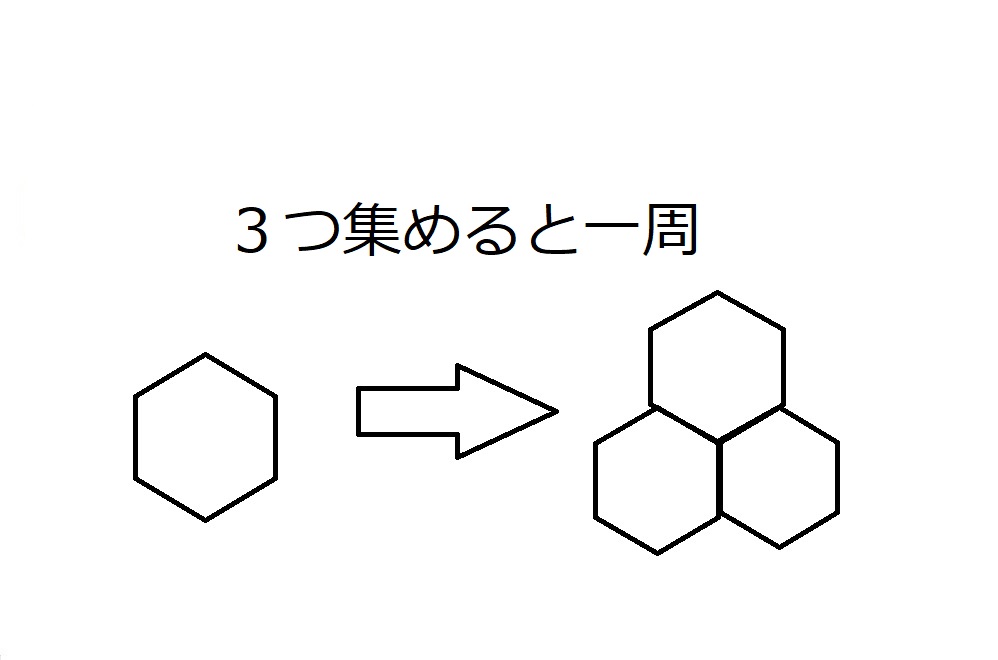
では正6角形は?
正六角形の1つの内角の大きさは120度です。
120は360の約数。
$360=120×3$
なので、正六角形3つでちょうど一周になり、敷き詰めができます。
では正七角形は?
実は、正七角形以上は、もう敷き詰めができないのです!
なぜか?
次の2つの事実を認めて説明しようと思います。
証明というよりは説明なので悪しからず。
① 敷き詰めができる正多角形の1つの内角の大きさは、360の約数になる
② 正三角形より、正四角形の方が1つの内角の大きさが大きいように、辺の数が多い正多角形ほど1つの内角の大きさは大きくなっていく。
では説明していきましょう。
正n角形について考えます。
この正n角形の1つの内角の大きさを$x$度としましょう。
360の約数は全部で24個しかありません。
具体的には、
1,2,3,4,5,6,8,9,10,12,15,18,20,24,
30,36,40,45,60,72,90,120,180,360
よって、$x$の候補はこの24個となります。
辺の数が一番小さい正多角形は正3角形なので、②より$x$は60より小さい値はとれません。
$x$が60より小さいと正多角形が作れないからです。
となると、$x$の候補は$x=60, 72, 90, 120, 180, 360$です。
先ほど試してみた通り、$x=60, 90, 120$のときは敷き詰めができました。
$x=72$は何でしょうか?
正三角形と正方形の間に正3.5角形とかはないので、$x=72$となる正多角形は存在しません。
また、$x=180$はもはや直線です。
$x=360$も正多角形ではありえません。
以上のことから、敷き詰めができるのは、$x=60, 90, 120$のときのみ。
具体的には、正三角形、正四角形、正六角形のみとなります。
敷き詰めができる正多角形についての証明
敷き詰めができる正多角形は、正三角形、正方形、正六角形のみ。
先ほどの説明で十分納得できた!という方はここの解説は読み飛ばしていただいてOKです。
次の見出しに進んでください。
高校の知識を使うと、先ほどの説明をもう少しスタイリッシュに表現できるので、
補足的なノリでもう少し詳しいことを解説しようと思います。
でもちょっと難しいです。
正n角形が敷き詰めをすることができるのは、n=3, 4, 6のときのみである
証明
正n角形の1つの内角の和は、
$\dfrac{180×(n-2)}{n}$である。
敷き詰めができるためには、これが360の約数でなければならないので、
$\dfrac{180×(n-2)}{n}×m=360$
となる。ただし、$m$は自然数。
$\dfrac{180×(n-2)}{n}×m=360$より、
$180(n-2)×m=360n$
両辺を180で割り、移項して整理する。
$mn-2n-2m=0$
これを$n$について降べきの順に整理すると、
$(m-2)n-2m=0$
$m-2$を共通因数としてくくりだしたいので、左辺に4を足し、4を引く
$(m-2)n-2m+4-4=0$
$(m-2)n-2(m-2)=4$
$(m-2)(n-2)=4$
ここで、$m-2, n-2$は自然数でなければならないので、
$(m-2, n-2)=)(1, 4), (2, 2), (4, 1)$である。
よって、$(m, n)=(3, 6), (4, 4, ), (6, 3)$
となり、$n=3, 4, 6$のみ。
したがって、敷き詰めができる正多角形は、正三角形、正方形、正六角形のみ
証明終了
補足です。
証明ではいくつか大学入試の重要テクニックが使われています。
① 因数分解。文字が多い時は、最低次数で降べきの順に整理。次数が同じなら、どれかに注目して降べきの順に整理。
② 整数問題は、掛け算にするか、大小関係でしぼるか、あまりで分類する。
→今回は掛け算にして絞り込みをしました。どういうことかというと、
$xy=4$という式があったとします。
$x, y$が実数なら、$x=7, y=\dfrac{4}{7}$でも$x=\sqrt{2}, y=2\sqrt{2}$でも、なんでもありで、答えは絞り切れません。
しかし、$x, y$に自然数という条件が付いていれば、$x=1, y=4$と$x=2, y=2$と$x=4, y=1$しかありえなくなります。
このように、「整数」という条件や、「自然数」という条件は大きな武器になりえるのです!
このあたりのことは、「問題を解く楽しみ」のカテゴリーでそのうちまとめていこうと思うので、どうぞご期待ください。
$\dfrac{180×(n-2)}{n}$
多角形の1つの内角を求める公式、役に立つことあるんだ!
と思っていただければとても嬉しいです。
ネットの伸縮性について
今までの話では、サッカーゴールのネットの可能性として、
正三角形、正方形、正六角形しかありえないということを確認しました。
じゃ、なんでその3択から正六角形が選ばれているんだよ!!
というところを解説していきます。
これは、ゴールの瞬間をダイナミックに見せたい!という気持ちが作用します。
どういうことかというと、例えばサッカーゴールがネットではなく壁だったとします。
ゴールしたボールは壁に打ち返された後、重力に逆らいきれず無慈悲にグラウンドへ叩きつけられます。
なんかむなしくないですか?
せっかくのゴールが壁打ちと同じなんて、こんなのってないです。
しっかりネットに受け止めてほしいものです。
ではいいネットはどんなネットでしょう。
それは、よく伸びるネットです。
ゴールしたボールがまるでネットに突き刺さっているかのごとく伸びてくれれば、
ゴールがよりダイナミックに見えて、迫力が増します。
そのためにはどんな形がいいでしょう。
敷き詰めができる正多角形は3種類しかないので、順に検討していきます。
まず正三角形。
これはすべての図形の中で最も変形しにくい図形です。
三角形最強と覚えておきましょう。
最も変形しにくいので、最も伸びにくいです。
よって正三角形はゴールネットに不向きです。
では、正四角形はどうでしょうか?
以下のgifをご覧ください。

伸びます!!
四角形は伸びるのです!
しかも対角線方向、2つの方向に延びます。
三角形とは大違いです!
しかも四角形のネットは作りやすいです!
このような理由から、長らく四角形のネットが使われていたわけです。
では、最後に正六角形の場合を見ていきましょう。

めっちゃ伸びます!
もうびっくりするくらい伸びます!!
どのくらい伸びるかというと、なんと3方向に伸びます!!
四角形よりも断然伸びるのです。
サッカーゴールのネットが正六角形な理由
いかがでしたか?
今回はサッカーゴールのネットが正六角形である理由を2つの観点から説明しました。
理由① 敷き詰めができる正多角形は、正三角形、正方形、正六角形の三種類の身
理由② その三種類の中で最もいろんな方向に伸びるのは正六角形
理由①、②から、ゴールの瞬間を最もダイナミックに表現できるネットは正六角形のネット
以上の流れを楽しんでいただけたのならとっても嬉しいです。
では、最後にもう一度ゴールの瞬間を見ておきましょう。
ダイナミックですね!!


コメント