正規部分群の定義の必然性を考える

ガロア理論の主役、群論の華と言っても過言ではない正規部分群。

初学だと、なんであんな定義になっているのか謎だと思います。

そこで今回は、剰余類に群構造を持たせるための条件という切り口から正規部分群の定義のなぜに答えていこうと思います。

正規部分群の定義

まずは正規部分群の定義を述べておきます。

この$gHg^{-1}=H$という条件をなぜ考えようと思ったのか、なぜこんなもんが必要なのか。

今回はその疑問に答えていきたいと思います。

端的に言うと、それは剰余類を集めた集合$G/H$に

群構造を持たせようとすると、必然的に

$gHg^{-1}=H$

という条件が出てくる、

といった感じになります。

なんで$G/H$に群構造を持たせたいと思うのかは、

ガロア理論のアイデアに古典的にアプローチすると見えてきます。

概要だけ述べておくと、

①　方程式を解くということは係数の世界を広げるということ

②　また、ラグランジュ・リゾルベントを用いて対称性に着目していく視点も有効

③　対称性は群で表される。

④　係数の世界を広げていく作業と、対称性を高めていく作業が逆向きに対応している！（ガロア理論の基本定理）

⑤　係数の世界を広げる際に、何乗根の数を添加したかと、

　　集合$G/H$の要素の個数が対応しているっぽい

　　↑方程式が解けるための必要十分条件

⑥　$G/H$の性質を記述するのに群構造を用いたい

　　↑方程式が解けるための必要十分条件を数学的に記述したい

といった流れになります。

詳しくは以下の記事をご覧ください。

では先に進んでいきましょう！

剰余類のおさらい

剰余類の定義をおさらいしておきましょう。

そして、$H$による$G$の左剰余類を全てあつめた集合を$G/H$で表すのでした。

あえて表すなら、$G/H$の元は集合で、みな$gH$のような形をしていますから、

$G/H=\lbrace aH \mid a\in G\rbrace$

となります。

群は一般には交換法則が成り立たないので、

$g$が$H$の右側にいるのか左側にいるのかは結構重要です。

$gH\neq Hg$に留意しておきましょう。

なぜ剰余類があんな定義になっているのかは、

体育の授業の「出席番号順３列で整列！」

を一般化しているという視点で考えると納得できます。

そのあたりの議論に興味がある方はぜひ以下の記事をご覧ください。

剰余類を集めた集合に群構造をもたせる

演算〇についての群$G$と、その部分群$H$を考えます。

剰余類を集めた集合は、

$G/H=\lbrace gH \mid g \in G \rbrace$

です。

$G/H$に群構造を持たせるためには、これがある演算について

群の条件３つを満たしていることを示さなければなりません。

ここで問題が発生します。

仮定より$G$は群なので、

$g_1, g_2 \in G$をとってこれば

必ず$g_1 〇 g_2 \in G$であり、$G$は必ず〇について閉じているというのが前提です。

しかし$G/H$ではいきなり同じ議論を展開することはできません。

なぜか？

$g_1H, g_2H \in G/H$を取ってくるところまではOKなのですが、

$g_1H$　と　$g_2H$　は集合です。

$G$の元については演算〇が機能することが保証されていますし、

それが群構造を持つことも保証されています。

しかし、

$g_1H$　と　$g_2H$　についてはそもそも演算が定義されていません。

なので、自分でうまく演算を定義してあげないといけないのです。

$g_1H$　と　$g_2H$　の演算を表す記号を、例えば$*$としましょう。

すると、$G/H$が$*$について群であるためには、

$*$について閉じていないといけません。

それを数式で表すと、

$g_1H * g_2H \in G/H$

となります。

$G/H=\lbrace gH \mid g \in G \rbrace$

だったので、

要するに、$g_1H, g_2H \in G/H$に対して、

$g_1H * g_2H=g_3H$

となるような$g_3 \in G$が必ず存在しなければなりません。

そのように演算$*$をうまく定義してあげなければならないわけです。

$G$は群ですから、必ず$g_1〇g_2 \in G$です。

最も素朴に考えると、

$g_1H * g_2H=g_3H$

について$g_3=g_1〇g_2$として

$g_1H * g_2H=g_1〇g_2H$

とするのが妥当なように感じます。

さて。

いま我々は$*$という演算を自分たちで作りました。

新たな演算を自分で作ったときは、必ずあることを確認しないといけないのでした。

それは、well-definedかどうか。

well-definedに馴染みなない方は、以下の記事をご覧ください。

ここからは具体的に考えていきましょう。

３次の置換群$S_3$を考えます。

３次の置換群とは、３個の並べ替え全体を表す集合で、群構造を持ちます。

３個の並べ替えは３！＝６通りあり、具体的には

の６つです。

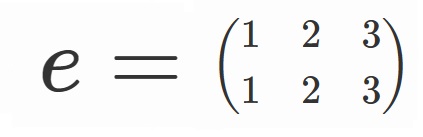
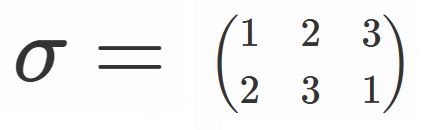
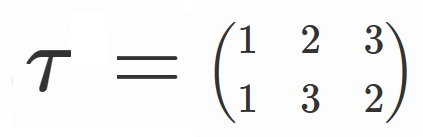
と定めると、

$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$

となります。

並べ替えの合成〇についての演算表は以下のようになります。

演算表から、$S_3$が〇について閉じていること、

結合法則が満たされること、単位元があること、逆元があること

が確認され、$S_3$が〇について群であることが分かります。

ここで、$H_1=\lbrace e, \tau \rbrace$

とします。

$e〇e=e, e〇\tau =\tau 〇e=\tau, \tau〇\tau=e$

なので、$H_1$は$S_3$の部分群です。

ここで、$S_3/H_1$を考えましょう。

$eH_1=\lbrace e〇e, e〇\tau \rbrace=H_1$

$\sigma H_1=\lbrace \sigma 〇e, \sigma 〇\tau \rbrace=\lbrace \sigma, \tau \sigma^2 \rbrace$

$\sigma^2 H_1=\lbrace \sigma^2 〇e, \sigma^2 〇\tau \rbrace=\lbrace \sigma^2, \tau \sigma \rbrace$

$\tau H_1=\lbrace \tau 〇e, \tau 〇\tau \rbrace=\lbrace \tau, e \rbrace=H_1$

$\tau \sigma H_1=\lbrace \tau \sigma 〇e, \tau \sigma 〇\tau \rbrace=\lbrace \tau \sigma, \sigma^2 \rbrace=\sigma^2 H_1$

$\tau \sigma^2 H_1=\lbrace \tau \sigma^2〇e, \tau \sigma^2〇\tau \rbrace=\lbrace \tau \sigma^2, \sigma \rbrace =\sigma H_1$

なので、

$S_3/H_1=\lbrace H_1, \sigma H_1, \sigma^2 H_1 \rbrace$

となります。

先ほど考えた演算$*$

$g_1H * g_2H=g_1〇g_2H$

を$S_3/H_1$で考えてみましょう。

例えば、

$\sigma H_1* \sigma^2 H_1=\sigma 〇\sigma^2 H_1=eH_1=H_1$

です。

さて、これはwell-definedになっているでしょうか？

すなわち、代表元を取り換えても同じ結果になるでしょうか？

先ほどの計算結果より、

$\sigma H_1=\tau \sigma^2 H_1$

$\sigma^2 H_1=\tau \sigma H_1$

でした。

well-definedであるためには、代表元を取り換えても同じものに対応付けられないといけないので、

$\tau \sigma^2 H_1 * \tau \sigma H_1=\sigma H_1 * \sigma^2 * H_1$

でなければなりません。

実際に計算してみましょう。

$\tau \sigma^2 H_1 * \tau \sigma H_1=\tau \sigma^2 〇\tau \sigma H_1=\sigma^2 H_1$

あぁ！！

$\tau \sigma^2 H_1 * \tau \sigma H_1 \neq \sigma H_1 * \sigma^2 * H_1$

です！！

ゆえに、何も考えずに$G/H$に

$g_1H * g_2H=g_1〇g_2H$

という演算を定義しても、

well-definedにならないということが分かりました。

$g_1H * g_2H=g_1〇g_2H$

がwell-definedになるためには、なんらかの条件を付けないといけないようです。

ではどんな条件を付けるとよいのでしょうか？

「代表元を取り換えても同じ行き先にたどり着く」ということを手掛かりに考えていきましょう。

これを数式で翻訳すると、

「$g_1H=g_1’H, $ 　$g_2H=g’_2H$のとき、$g_1 〇 g_2 H=g’_1 〇 g’_2 H$」

となります。

もう少し議論を進めていきましょう。

$g_1H=g_1’H$について考えます。

これは、

$\lbrace g_1h \mid h \in H \rbrace=\lbrace g’_1 h \mid h \in H \rbrace$

ということを意味しており、

要するに$g_1h_a \in g_1 H$に対して

$g_1h_a=g’_1h_b$

となる$h_b \in H$が必ず存在するということです。

$H$は群なので、必ず逆元をもちます。

$h_a$の逆元$h_a^{-1}$を

$g_1h_a=g’_1h_b$

の両辺に右から合成しましょう。

$g_1h_ah_a^{-1}=g’_1h_bh_a^{-1}$

$g_1 e= g’_1h_bh_a^{-1}$

$g_1=g’_1h_bh_a^{-1}$

ここで、$H$は群なので、$h_ah_b^{-1} \in H$

でなければなりません。

つまり、

$g_1H=g_1’H$という条件は、

$g_1$　に対して　$g_1=g_1’h_1$となる$h_1 \in H$が必ず存在する、

と言い換えることができます。

同じように、

$g_2H=g’_2H$

という条件は、

$g_2$　に対して　$g_2=g_2’h_2$となる$h_2 \in H$が必ず存在する、

と言い換えることができます。

これらのことから、

「$g_1H=g_1’H, $ 　$g_2H=g’_2H$のとき、$g_1 〇 g_2 H=g’_1 〇 g’_2 H$」

という文言は、

「$g_1=g’_1h_1, $ 　$g_2=g’_2h_2$のとき、$g_1 〇 g_2 H=g’_1 〇 g’_2 H$」

と言い換えることができます。

さて、$g_1 〇 g_2 H=g’_1 〇 g’_2 H$について考えましょう。

いま、$g_1〇g_2=(g’_1h_1)〇(g’_2h_2)$

なので、

$g_1〇g_2H=(g’_1h_1)〇(g’_2h_2)H$

です。

そのため、

$g_1 〇 g_2 H=g’_1 〇 g’_2 H$

を成り立たせるためには、

$(g’_1h_1)〇(g’_2h_2)=g’_1g’_2h_3$

となる$h_3 \in H$が存在すればよいことになります。

そのためにどんな条件を追加すればよいでしょうか？

手掛かりは、$H$が群であるということです。

すなわち、$h_1〇h_2 \in H$

です。

$h_3=h_1〇h_2$と定めたいところ。

そのためには、

$(g’_1h_1)〇(g’_2h_2)=g’_1g’_2h_3$

の左辺について、

$h_1$　と　$g’_2$　が交換可能であればよいと分かります。

$(g’_1h_1)〇(g’_2h_2)=g’_1g’_2h_3$

について、〇を省略せずにかくと、

$(g’_1〇h_1)〇(g’_2〇h_2)=g’_1〇g’_2〇h_3$

です。

この式に、$h_1〇g’_2=g’_2〇h_1$

という条件を追加して議論を進めます。

$(g’_1〇h_1)〇(g’_2〇h_2)=g’_1〇g’_2〇h_3$

について、結合法則より

$g’_1〇h_1〇g’_2〇h_2=g’_1〇g’_2〇h_3$

です。さらに

$h_1〇g’_2=g’_2〇h_1$

より、

$g’_1〇g’_2〇h_1〇h_2=g’_1〇g’_2〇h_3$

よって、

$h_1〇h_2=h_3$と定めれば、

「$g_1=g’_1h_1, $ 　$g_2H=g’_2h_2$のとき、$g_1 〇 g_2 H=g’_1 〇 g’_2 H$」

を成立させることができます。

ここまでの議論をまとめると以下のようになります。

ここからは、

$g_1〇h_1=h_1〇g_1$

という条件をさらに深めていきましょう。

いま$g_1$は固定されていて、$h_1$は$H$の元全体を動きます。

したがって、

$g_1〇h_1=h_1〇g_1$

は

$g_1H=Hg_1$

と言い換えることができます。

この両辺に$g_1$の逆元$g_1^{-1}$を合成すると、

$g_1Hg_1^{-1}=Hg_1g_1^{-1}$

となり、

$g_1Hg_1^{-1}=H$

です。

正規部分群の定義に他なりません！！！

まとめ

いかがでしたか？

・ガロア理論を進めるうえで、$G/H$が群としての構造をもつための条件が知りたくなる

・$G/H$にwell-definedな演算を定義するためには必然的に$gHg^{-1}=H$という条件が出現する

・ゆえに、$gHg^{-1}=H$を満たす部分群$H$を正規部分群と呼ぶことにしよう！

という流れを楽しんでいただければと思います。

ではまた次回の記事でお会いしましょう！！

参考

画像素材提供（アイキャッチ）：Gerd AltmannによるPixabayからの画像