大学数学を習っていると、いつかはwell-definedという概念と出会います。
なんでこんなものを考えるのかよく分からんランキングでも上位に入る意味不明概念です(マスタノ調べ)
今回は、well-definedとは何か、なぜ必要なのかといったことを、高校生の文化祭の運営会議を例に解説していきたいと思います。
その際に大切な考え方は、代表元に依らないかどうか調べるという発想になります。
イメージと直感で分かりやすく大学数学をつかんでいこう!
という試みですので、そのつもりでご覧ください。
文化祭の出し物決めようぜ!
在りし日の高校生活まで記憶をさかのぼらせましょう。
僕の高校では、文化祭の出し物は以下のような手順で決まっていました。
① クラスで意見をまとめ、やりたいジャンルの案を出す(模擬店とか、舞台発表とか)
② 学年ごとにクラスの代表議員を集め、クラスの意見を集約する
③ 代表議員たちによる文化祭運営会議で学年ごとのジャンルが決まる
④ そのジャンルに基づいて文化祭を実行し、各学年でクオリティを競う
図にすると以下のような感じです。
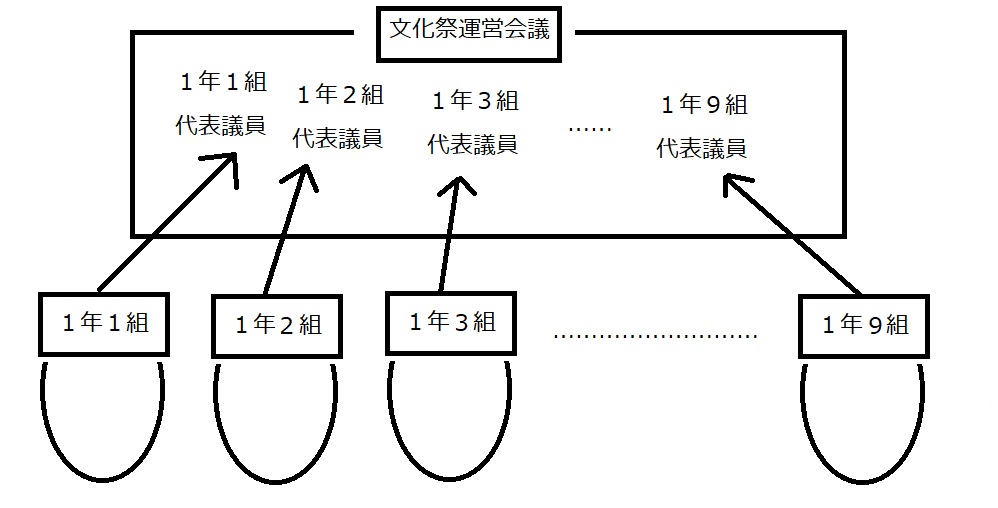
さて、皆さんは1年2組の生徒です。
クラスでの話し合いの結果、1年2組では「模擬店をやりたい」という方向で意見がまとまりました。
クラスの代表議員はAさん。
Aさんは文化祭運営会議で「1年2組では模擬店をやりたいという案が出ています」と報告してくれるでしょう。
ここまでは全く問題ないです。
しかし、例えば文化祭運営会議の日にAさんが風邪で欠席してしまったらどうでしょう?
代理のBさんが文化祭運営会議に出席することになります。
ここで、Bさんが会議で「1年2組では舞台発表をやりたいという案が出ています」
とか言い出したら大問題です。
誰を代理に立てたとしても、「1年2組では模擬店をやりたいという案が出ています」
と発言してくれる状況でないと、「クラスの意見がまとまった」とは言い難いですよね。
はい。
今回伝えたい内容の本質部分は終わりました!!
well-definedの説明
数学にはいろいろな定義が出てきます。
例えば、「3つの角が等しい三角形を正三角形という」とか、
「ある数$a$に対して、二乗して$a$になる数を$a$の平方根という」とか、
こういうのは定義です。
定義は言ったもの勝ちなイメージがあるかもしれませんが、
やみくもになんでも定義を与えていればそれでいいのかというと、そういうわけではありません。
ある程度の規範が必要になります。
特に写像や演算を自分で考えて使う場合は注意が必要です。
写像(中学や高校で関数と呼んでいるもの)とは、簡単に言えば対応付けのこと。
あるものを決めると、対応先がただ一つに定まるような対応関係を写像(あるいは関数)といいます。
対応先がただ一つでないと、写像とは言えません。
あるものを定めると、対応先がただ一つに定まる。
これが写像だ!となんとなく理解してくださればそれでOKです。
数学で証明を進める際に、自分で考えた対応付けを利用したくなることが結構あります。
しかし、勝手に考えただけの対応は、必ずしも写像になっているとは限りません。
要するに、対応先が2つ以上存在していないかどうか確かめないといけないのです。
それを確かめた状態のことをwell-definedといいます。
特に集合の集合を考える際にはwell-defindかどうかの確認がとても大切になります。
例えば、高1学年という集合は、1年1組、1年2組、…、1年9組からなる集合です。
$\lbrace 高1学年 \rbrace=\lbrace 1年1組, 1年2組, 1年3組, \cdots, 1年9組 \rbrace $
ここで、1年1組や1年2組も集合です。
このように、高1学年という集合は、集合の集合と捉えることができます。
ここに対応付けを導入します。
このとき、
自分で作った対応付けがwell-definedだと、ちゃんと写像として成立する、
といったイメージでいてください。
先ほどの文化祭の例で考えましょう。
1年2組のどの人を代表議員に選んだとしても、
必ず「1年2組では模擬店をやりたいという案が出ています」と発言してくれる状況が
well-definedな状況です。
1年2組と「模擬店をやりたい」がちゃんと対応するからです。
これに対して、1年2組の代表議員の代理としてAさんを選んだ場合とBさんを選んだ場合で
違う発言が出てしまう状況、言い換えれば、
代表議員を誰にするかによって意見が変わってしまう状況は
well-definedとは言いません。
1年2組に対して、「模擬店をやりたい」と「舞台発表がやりたい」の2つの意見が対応してしまうからです。
ちなみに、AさんやBさんを数学の言葉では代表元といいます。
well-definedについてなんとなくイメージができてきたかと思いますので、
ここで具体例を考えていこうと思います。
well-definedになっていない例
well-definedを考えるにあたっては、
well-definedになっている例よりも、
うまくいっていない例を観察した方が理解が深まる気がします。
そこで、初めに有理数の足し算を考えましょう。
例えば、
$\dfrac{2}{3}+\dfrac{4}{5}$
を考えましょう。
いうまでもなく、
$\dfrac{2}{3}+\dfrac{4}{5}=\dfrac{10}{15}+\dfrac{12}{15}=\dfrac{22}{15}$
です。しかし、小学生が初めて分数の計算を習うと、
$\dfrac{2}{3}+\dfrac{4}{5}=\dfrac{2+4}{3+5}=\dfrac{6}{8}=\dfrac{3}{4}$
という間違いをしがちです。
でも、これってなんで間違いだとされているのでしょうか?
分数の計算を$\dfrac{b}{a}+\dfrac{d}{c}=\dfrac{b+d}{a+c}$と定めていたのなら、
別に
$\dfrac{2}{3}+\dfrac{4}{5}=\dfrac{2+4}{3+5}=\dfrac{6}{8}$
でも問題ありません。
しかし、実際には分数の足し算の定義として
$\dfrac{b}{a}+\dfrac{d}{c}=\dfrac{b+d}{a+c}$
が採用されることはありません。なぜか?
それは、well-definedにならないからです。
記号が紛らわしいので、+の代わりに$\dot{+}$を用いることにします。
小学生がよく間違える足し算を$\dot{+}$で表します。
$\dfrac{b}{a} \dot{+} \dfrac{d}{c}=\dfrac{b+d}{a+c}$
がwell-definedでないことを確認します。
この定義で考えると、
$\dfrac{2}{3} \dot{+} \dfrac{4}{5}=\dfrac{2+4}{3+5}=\dfrac{6}{8}=\dfrac{3}{4}$
より、
$\dfrac{2}{3} \dot{+} \dfrac{4}{5}=\dfrac{3}{4}$
です。
一方で、$\dfrac{2}{3}$を表す有理数は他にも沢山あります。
$\dfrac{2}{3}=\dfrac{4}{6}=\dfrac{6}{9}=\dfrac{8}{12}=\cdots$
です。同様に、
$\dfrac{4}{5}$を表す有理数も沢山あります。
これを踏まえたうえで、例えば
$\dfrac{8}{12} \dot{+} \dfrac{16}{20}$
を考えましょう。
$\dfrac{8}{12}=\dfrac{2}{3}, \dfrac{16}{20}+\dfrac{4}{5}$
ですので、当然
$\dfrac{8}{12} \dot{+} \dfrac{16}{20}=\dfrac{2}{3}\dot{+} \dfrac{4}{5}$
であって欲しいところです。
しかし実際には、
$\dfrac{8}{12} \dot{+} \dfrac{16}{20}=\dfrac{8+16}{12+20}=\dfrac{20}{32}=\dfrac{5}{8}$
です。
$\dfrac{2}{3}$を表す有理数として、
$\dfrac{2}{3}$を採用した場合と$\dfrac{8}{12}$を採用した場合で異なる答えが導かれてしまいました。
ゆえに、小学生がよく間違える足し算$\dot{+}$は
well-definedではありません。
well-definedな例
我々が今まで学校で習ってきたものは多くがwell-definedなので、
あえて例を出すまでもないですが、
先ほど有理数の足し算の例を出したので、
これで説明しようと思います。
$\dfrac{b}{a}+\dfrac{d}{c}=\dfrac{bc+ad}{ac}$
とします。
これがwell-definedであることを確認しましょう。
ある数$s$をとり、
$\dfrac{b}{a}$の分子・分母を$s$倍しましょう。
$\dfrac{b}{a}=\dfrac{bs}{as}$
です。
同様に、ある数$t$をとり、
$\dfrac{d}{c}$の分子・分母を$t$倍します。
$\dfrac{d}{c}=\dfrac{dt}{ct}$
です。
$\dfrac{b}{a}+\dfrac{d}{c}=\dfrac{bs}{as}+\dfrac{dt}{ct}$
を確かめましょう。
$\dfrac{bs}{as}+\dfrac{dt}{ct}$
$=\dfrac{(bs)(ct)+(as)(dt)}{(as)(ct)}$
$=\dfrac{(bc+ad)st}{acst}$
$=\dfrac{bc+ad}{ac}$
$=\dfrac{b}{a}+\dfrac{d}{c}$
よって、
$\dfrac{b}{a}+\dfrac{d}{c}=\dfrac{bs}{as}+\dfrac{dt}{ct}$
となり、+は代表元の取り方に依らないためwell-definedとなります。
まとめ
いかがでしたか?
・well-definedとは、誰を集合の代表にしても意見が変わらないということ
・自分で対応関係を作る場合はwell-definedであることの確認が大切
・対応関係がwell-definedなとき、はじめてそれは写像として機能することになる
以上のことを押さえていただければと思います。
いよいよ次回は正規部分群の定義について触れていこうと思いますので、ご期待ください。
参考
画像素材提供(アイキャッチ):Peggy und Marco Lachmann-AnkeによるPixabayからの画像

コメント