ピタゴラス数の公式の導出は、いろいろある!
前回までのおさらい
ピタゴラス数とは、$a^2+b^2=c^2$が成り立つ3つの自然数です。
それに互いに素、という条件をつけたものを原始ピタゴラス数といいます。
原始ピタゴラス数を無限にゲットできる公式を導出しよう!というのが今までの取り組みでした。
文言でまとめると、こうです。
互いに素な3つの自然数$a, b ,c$を考える。
このとき、$a^2+b^2=c^2$となるような
自然数の組$(a, b, c)$を求める公式を導出する。
公式を導出したり証明したりするときは、
どの条件に着目するか
が極めて重要になります。
ピタゴラス数の問題の場合は、緑マーカーと黄色マーカーが条件です。
前回の記事では、緑マーカーの条件に着目して公式を導出しました。
今回は、黄色マーカーに着目して別解を紹介しようと思います。
このやり方だと、円上の点で、$x, y$がともに有理数であるようなものを探すことに帰結されます。
僕はこっちのやり方の方が、なんか大学数学っぽくて好きです。
前回のまで記事はこちらを参照ください。
前々回

前回

公式の導出(直角に着目した場合)
互いに素な3つの自然数$a, b, c$を考える。
このとき、$a^2+b^2=c^2$となる自然数の組$(a, b, c)$を求める公式を導出する
~脳内会議~
今回は、$a^2+b^2=c^2$に着目して考えていきます。
三平方の定理の逆から、直角三角形が出現します。
この直角がポイントです!
前回の記事では原始ピタゴラス数を「整数問題」と捉えて処理しましたが、
今回は「図形の問題」と捉えて処理します。
数学Aの図形の性質の問題や、
数学Ⅱの図形と方程式の問題を解くときに有効な考え方を発動します。
それは、
直角・直径・円は3点セット!というテクニックです。
どういうことでしょうか?
これは、円周角の定理が関係しています。
円周角は中心角の半分になるよ!というあれです。
特に、中心角が180°の場合を考えましょう。
円周角は必ず90°になります。
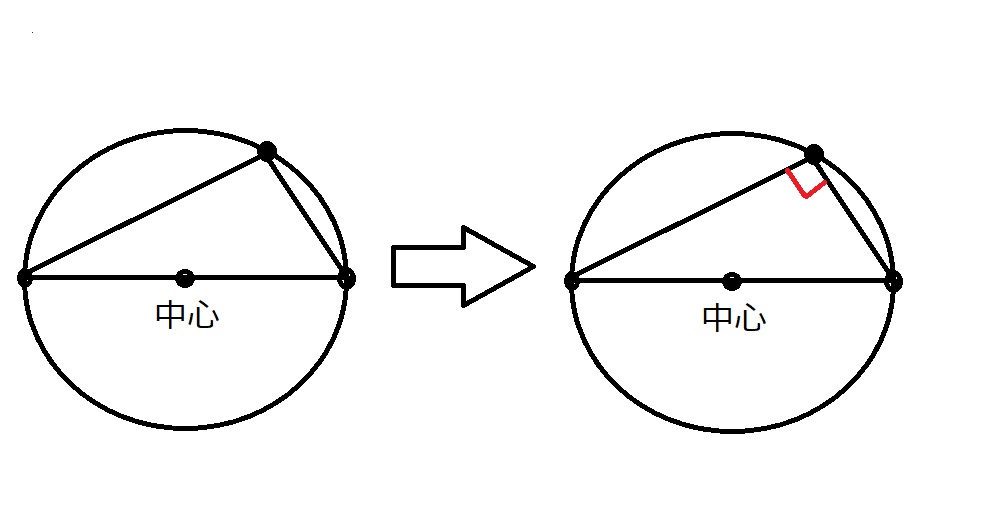
大切なこととして、円周角の定理は逆が成立します。
つまり、2定点A, Bが与えられて、Cが動点であるとき、
∠ACBが90°ならば、C の軌跡は線分ABを直径とする円
になります。
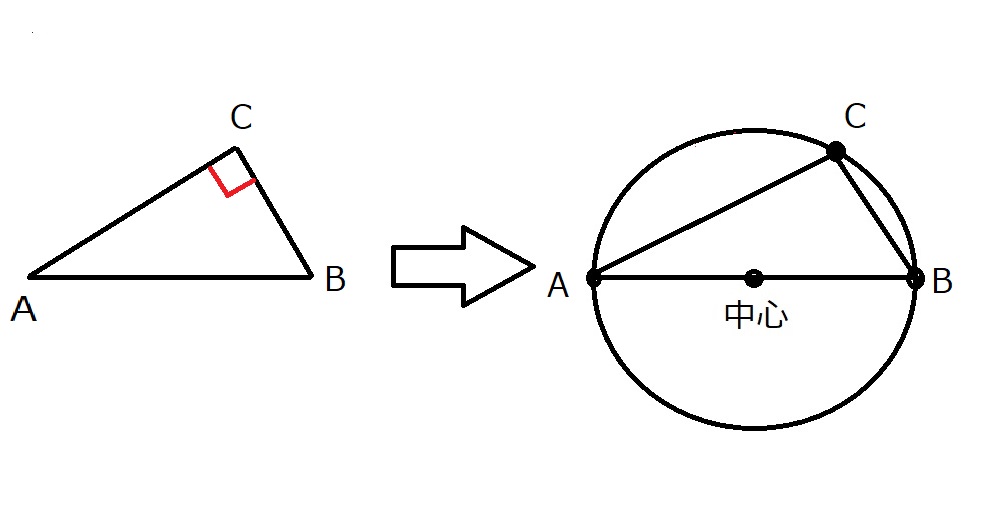
何もないところから直角だけを頼りに円を召喚できるという魔法のようなテクニックです。
直角・直径・円はワンセット。
どれが2つがそろったら残り1つを召喚できます。
今回はこのテクニックに基づいて原始ピタゴラス数の公式を導出していきます!
なお、3つの数$a, b, c$が「原始」ピタゴラス数であるには、
公式を導出した後に「互いに素」であることを確認せねばなりませんが、
その確認作業が結構長く、加えて前回の記事でほぼ同じようなことをしているので、
今回はサボる、という決断をしました笑。
(原始)ピタゴラス数という表現が出てきますが、カッコがついているのは
互いに素の確認をサボったからと認識してください。
(導出)
$a^2+b^2=c^2$の両辺を$c^2$で割る。
すると、$(\dfrac{a}{c})^2+(\dfrac{b}{c})^2=1^2$となる。
これは原点を中心とする半径1の円の方程式$x^2+y^2=1$に
$x=\dfrac{a}{c}, y=\dfrac{b}{c}$を代入したものに他ならない。
($\dfrac{a}{c}, \dfrac{b}{c}は有理数$)
つまり、原始ピタゴラス数を求める過程は、
$x^2+y^2=1$の有理数解を求めることとに帰結される。
ここで、円上の点$(-1, 0)$を通る傾きが$m$である直線を考える。
$y=m(x+1)$である。
$y=m(x+1)$と$x^2+y^2=1$の交点のうち、
$x座標の値とy座標の値$がともに有理数となるようなものを考えればよい。
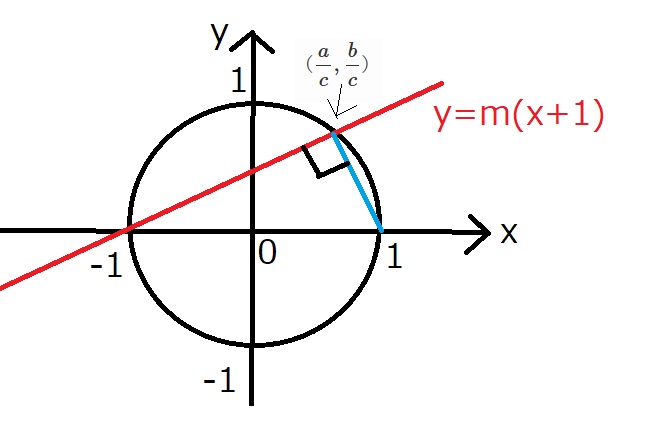
$y=m(x+1)$を$x^2+y^2=1$に代入して整理すると、
$(m^2+1)x^2+2m^2x+m^2-1=0$となる。
因数分解すると、
$\lbrace (m^2+1)x+(m^2-1) \rbrace (x+1)=0$となり、←たすき掛けしました。
$x=\dfrac{1-m^2}{1+m^2}, -1$となる。
$x=\dfrac{1-m^2}{1+m^2}$に着目する。
このとき、
$y=m(x+1)$に$x=\dfrac{1-m^2}{1+m^2}$を代入して計算すると、
$y=\dfrac{2m}{1+m^2}$となる。
よって、
$(x, y)=(\dfrac{1-m^2}{1+m^2}, \dfrac{2m}{1+m^2})$
となる。
$x, y$がともに有理数であるためには、$m$が有理数であればよい。
$m=\dfrac{A}{B}$(これは既約分数)とおくと、
$(x, y)=(\dfrac{1-\dfrac{A^2}{B^2}}{1+\dfrac{A^2}{B^2}}, \dfrac{2\dfrac{A}{B}}{1+\dfrac{A^2}{B^2}})$
となる。これを整理すると、
$(x, y)=(\dfrac{B^2-A^2}{B^2+A^2}, \dfrac{2BA}{B^2+A^2})$
いま、$(x, y)=(\dfrac{a}{c}, \dfrac{b}{c})$であったので、
$\dfrac{a}{c}=\dfrac{B^2-A^2}{B^2+A^2}, \dfrac{b}{c}=\dfrac{2BA}{B^2+A^2}$となる。
よって、$a=B^2-A^2, b=2BA, c=B^2+A^2$とすればよく、
$(a, b, c)=(B^2-A^2, 2BA, B^2+A^2)$
である。
これによって(原始)ピタゴラス数を求めることができる。
(導出終了)
まとめ
いかがでしたか?
前回と比べてかなりスタイリッシュに公式を導けた気がします。
このように、同じ公式を導出するとしても、
どの条件に重きを置くかで解法は180°変わってきます。
それが数学の面白いところの1つですね。
また、今回公式を導出する途中で出てきた
$(x, y)=(\dfrac{1-m^2}{1+m^2}, \dfrac{2m}{1+m^2})$
という式には、もう少し深遠な秘密が隠されています。
それはまた数学Ⅲの積分を扱う際に紹介しようと思うので、ご期待ください。
ではまた次の記事でお会いしましょう!
コメント