1,4,9,16,25,36,49,…
今回は、これらの数について研究していきます!!
観察
まずは観察です!
1,4,9,16,25,36,49,…
次の数は?
もちろん64です。
どんな規則性で並んでいるかというと、
二乗の数が並んでいます!
$1^2, 2^2, 3^2, 4^2, 5^2, 6^2, 7^2, 8^2, \cdots, n^2, \cdots$
となります。
さて、これを観察するときの視点はいろいろありえますが、今回は足してみようと思います。
$1+4=5$ ←別に面白くない
$4+9=13$ ←別に面白くない
$9+16=25$ ←めっちゃ面白い!!!
$16+25=41$ ←別に面白くない
このように続いていきます。
さて。
きっと皆さん、こう思っているのではないでしょうか?
「面白いやつ」と「面白くないやつ」は一体何が違うんだよ!!
種明かしです。
二乗の数に注目してもう一度観察してみます。
$1^2+2^2=5$
$2^2+3^2=13$
$3^2+4^2=5^2$
$4^2+5^2=41$
どうですか?
$9+16=25$という式がいかにすごい式であるか伝わったと思います。
今回は、$a^2+b^2=c^2$
が成り立つ自然数$a, b, c$について研究していきましょう!!
このような数をピタゴラス数といいます。
余談ですが、$a^2+b^2=c^2$という式は、三平方の定理の式に他なりません。
つまり、三平方の定理は、逆が成立するのです!
三平方の定理の逆
自然数$a, b, c$が$a^2Lb^2=c^2$を満たすならば、三辺の長さが$a, b, c$である三角形は直角三角形になる
これの何がすごいかというと、直角を自由自在に作れる!という点です。
三平方の定理の逆と古代エジプト
研究からは少し脱線しますが、ここで三平方の定理の逆に関する小話をしようと思います。
昔の人々にとって、直角を作る、というのはめっちゃ重要な問題でした。
例えば、ピラミッド。
大きな建造物を作るとき、地面と直角になるように建てないとグラグラの危ないものになってしまいます。
目測でなんとなく直角っぽく作っても、それが本当に直角である保証はどこにもありません。
そこで数学の出番です。
まず、でかい縄で輪を作ります。
次に、先ほどの$3^2+4^2=5^2$という式を利用します。
$3+4+5=12$なので、縄の輪を12等分します。
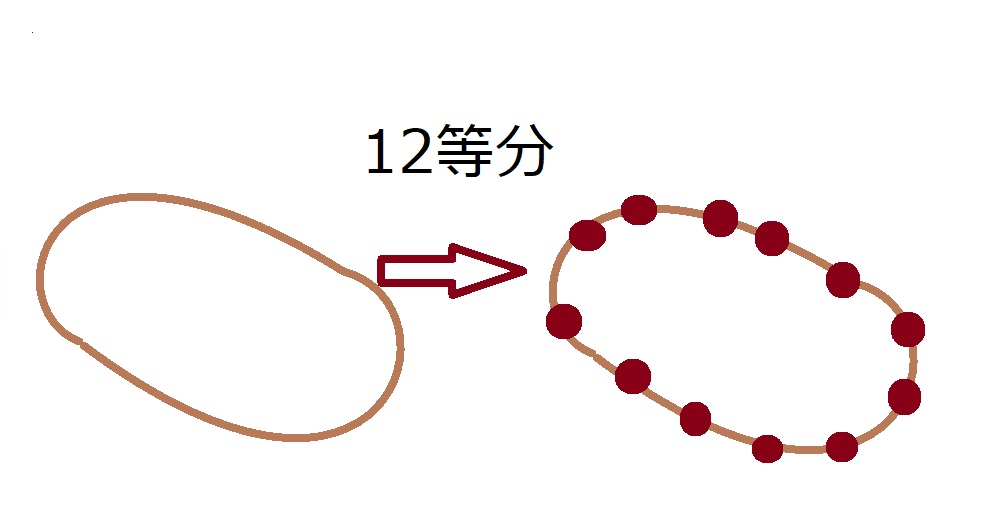
この輪を$3 : 4 : 5$に分けると、三平方の定理の逆から直ちに直角三角形を作ることができるのです!
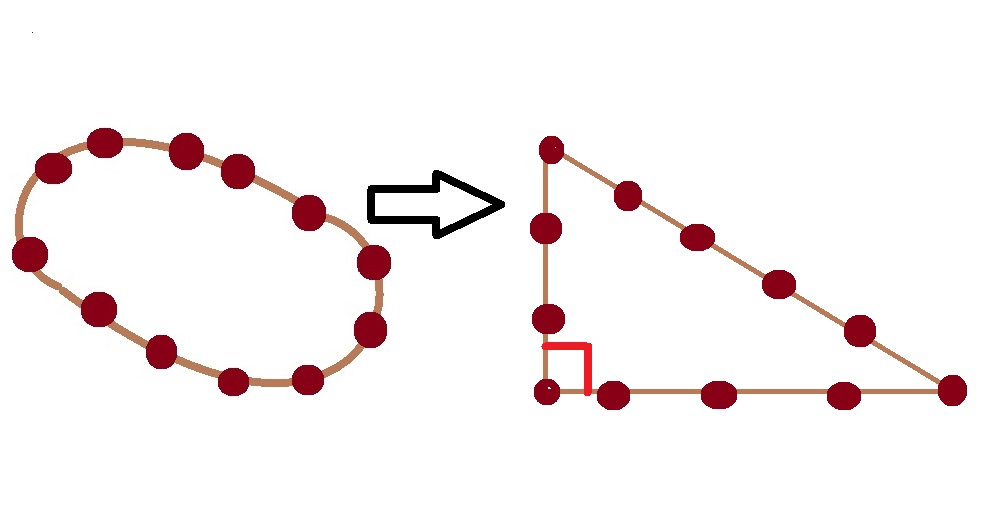
この直角三角形を用いて昔の人々は建物を地面と直角にしていたのです!
となみに、昔のエジプトには縄張り師というプロがいて、縄を使って角度や長さを測定していたそうです。
それで職業として成立するくらい、昔の人たちにとって直角は大切だったということですね。
そんな縄張り師さんたちを陰で支える数学が、三平方の定理の逆であり、ピタゴラス数です。
ピタゴラス数の研究を深めていきましょう!
観察その②
さきほどの縄張り師さんたちの例から、$3^2+4^2=5^2$の式は、$3, 4, 5$という長さが重要なのではなく、
$3: 4: 5$という比が大切なのだと分かりました。
つまり、比が$3: 4: 5$であれば$a^2+b^2=c^2$は成立するのではないか?という予想が立ちます。
試してみましょう。$a=6, b=8, c=10$ではどうでしょうか?
$36+64=100$
なりそう!!
$6^2+8^2=10^2$は成立することが分かりました。
このようにして、$3:4:5$の三角形と相似な三角形を用いれば、無限に$a^2+b^2=c^2$の式を作ることができそうです。
ですが。
ここで終わるわけにはいきません。
$3: 4: 5$以外に$a^2+b^2=c^2$となるものはないか?
ということが気になります。
そこで、ここから先は$a, b, c$が互いに素であるようなピタゴラス数を考えます。
互いに素とは、最大公約数が1であるということを表します。
さっきの例でいくと、$(a, b, c)=(6, 8, 10)$は、最大公約数が2であり、「互いに素」ではないので除外されます。
要するに、相似な人たちをひとくくりに同じものとみなすよ!ということです。
「互いに素」という条件を付けたピタゴラス数を原始ピタゴラス数といいます。
さて、3,4,5の他にどんな数が見つかるでしょうか?
例えば、5,12,13
というのがあります。
$25+144=169$で、$5^2+12^2=13^2$です。
が、この他の原始ピタゴラス数は、ちょっと自力じゃ見つかりません(泣)
なので、ひとまず次の段階に進みましょう。
規則性を見つける
$a^2+b^2=c^2$となる自然数$a, b, c$を探したところ、
$3, 4, 5$と$5, 12, 13$が見つかりました。
サンプル数2で規則性を見つけ出すのは至難の業ですが、
今回はサンプルを集めること自体がまぁまぁ困難なので、この2つをよりどころに頑張ります。
$3, 4, 5$と$5, 12, 13$をじっくり見つめています。
12,13という並びになにか神秘を感じるような気がしなくもありません。
3,4,5も5,12,13も、後半2つは連続する数になっているっぽいです!
証明
予想
互いに素である3つの自然数の組$(a, b, c)$で、$a^2+b^2=c^2$と$c=b+1$であるものが無数に存在する。
まずは$c=b+1$を$a^2+b^2=c^2$に代入してみましょう。
$a^2+b^2=(b+1)^2$より、左辺の$b^2$を右辺に移項すると
$a^2=2b+1$
つまり、$b=\dfrac{1}{2}(a^2-1)$となり、
$b=\dfrac{1}{2}(a+1)(a-1)$となります。
$b$は自然数なので、$(a+1)(a-1)$は偶数でなければなりません。
$a$が偶数だと$a+1, a-1$がともに奇数となり、$b$が自然数にならないので、
$a$は奇数と確定します。
$a=2m+1$と置きましょう。$m$は自然数です。
すると、$b=\dfrac{1}{2}(2m+1+1)(2m+1-1)$から
$b=2m(m+1)$となります。
このことから、
$(a, b, c)=(2m+1, 2m(m+1), 2m(m+1)+1)$となり、計算すると
$(a, b, c)=(2m+1, 2m^2+2m, 2m^2+2m+1)$
が求まります。
このことから、原始ピタゴラス数は無限に存在すると分かります。
ちなみに、$m=1$のときが$(a, b, c)=(3, 4, 5)$で、$m=2$のときが$(a, b, c)=(5, 12, 13)$です。
他にも、例えば$m=10$とかを代入すると、
$(a, b, c)=(21, 220, 221)$というなんか3進数っぽい原始ピタゴラス数が見つかります。
この$(21, 220, 221)$の直角三角形は、現実世界に存在したら大体勾配10%くらいの坂道なので、
結構ヤバ目の坂道となります。

まとめ
いかがでしたか?
二乗の数を研究していったらピタゴラス数に到着しました。
また、途中の小話では、縄張り師さんのことや、勾配のことを紹介しました。
実は、縄張り師さんの知見や、勾配の計算などは、
そのまま数Ⅰで習う三角比につながっていきます。
その周辺のこともまた別の記事で紹介していこうと思いますので、ご期待ください。
また今回、
$(a, b, c)=(2m+1, 2m^2+2m, 2m^2+2m+1)$
が求まりましたが、実はこの公式はまだ先があります。
というのも、今回の公式は$c=b+1$という極めて特殊な条件がついている場合のみ成立する式なのです。
(観察したサンプルが2つしかないので、特殊な場合しか見つけられなかったのは必然ですが)
数学者の目で今回のことを振り返ってみましょう。
次に何がしたくなるかというと、
$c=b+1$という条件がついていない、より一般的な公式をゲットしたい!
ということになります。
でも今回はここまで。
続きはまた次の記事でのお楽しみ。
次の記事はこちら


コメント