今回の記事では、部分群という概念について詳しく解説していきます。
新しい概念を理解するには、豊富な具体例が不可欠です。
部分群の定義の必然性を具体例を使って考察する点に重きを置きました。
部分群の定義
部分群について考える前に、まずは群(ぐん)の定義をおさらいしましょう。
(群の定義)
集合$G$にある演算$〇$が定義されているとする。
$G$が以下の条件を満たすとき、$G$を群(ぐん)という
①すべての$a, b, c \in G$について、$a〇 (b〇 c)=(a〇 b)〇 c$が成り立つ
(結合法則)
②すべての$a \in G$に対して、$ae=ea=a$となる$e \in G$が存在する
($e$を単位元という)
③すべての$a \in G$に対して、$ax=xa=e$となる$x \in G$が存在する
($x$を逆元という)
なぜ群という概念を考える必要があるのか、なぜ群がこのような定義になっているか
といった点に興味を持たれた方はぜひ以下の記事をご覧ください。

さて、ここからは部分群について話を進めていきます。
簡単に言うと、
ある群$G$の部分集合$H$もまた群となっているとき、
$H$を$G$の部分群といいます。
注意事項として、$H$は空集合$\phi$であってはいけません。
空集合には元が存在しないので、演算を定義することが自然ではないからです。
では、部分群の定義を紹介しましょう。
(部分群の定義)
集合$G$は演算〇について群となっているとする。
$G$の部分集合$H$が次の3つの条件を満たすとき、
$H$を$G$の部分集合という。
① $a, b \in H$ならば、$a〇 b \in H$
② $a \in H$ならば、$a^{-1} \in H$
③ $H$は空集合ではない
次の見出しでは、
部分群の定義がなぜこんな条件になっているのかを考えていきたいと思います。
部分群の定義の意味と具体例
部分群の定義を考察するうえでは、
「ある群$G$の部分集合$H$もまた群」
という条件をどう数式に落とし込むか考えることが大切です。
そこで、具体例を通して考えていきましょう。
$G_1=\lbrace \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5, 1 \rbrace$
とします。$\zeta_6$は1の6乗根を表しています。
$\zeta_6^6=1$である点に注意しましょう。
すると、$G_1$は掛け算×という演算について群になります。
まず$G_1$が掛け算について閉じているかどうか調べます。
演算表で確認しましょう。
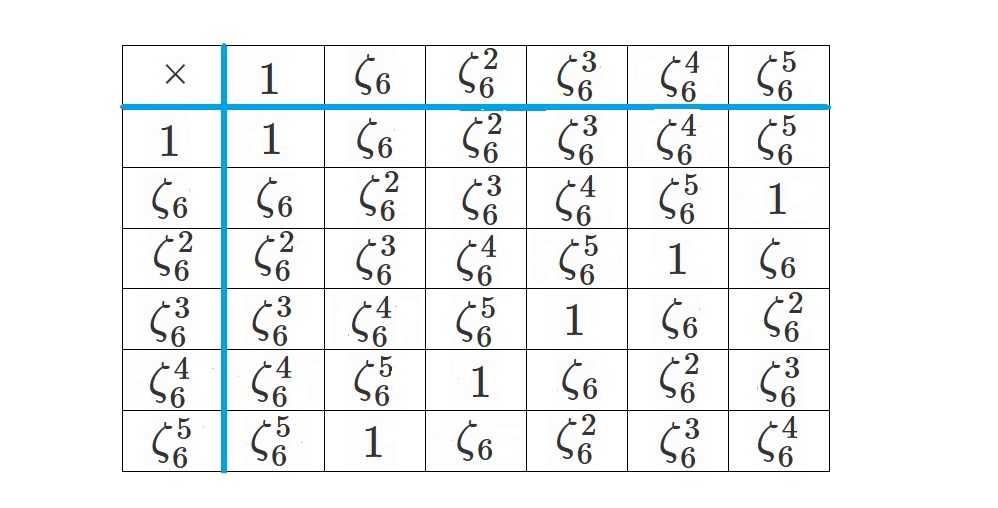
また、$G_1$の元は全て複素数なので、結合法則が成立することは自明です。
ゆえに$G_1$は群です。
ここで、$G_1$の部分集合$H_1$を考えます。
$G_1$の元は$6$つなので、部分集合は理論上$2^6$通り存在します。
例えば、
$H_1=\lbrace \zeta_6^2, \zeta_6^5 \rbrace$
としてみましょう。
これは掛け算×について群になるでしょうか?
答えはNOです。
$\zeta_6^2×\zeta_6^5=\zeta_6^{7}$
となり、$\zeta_6^6=1$に注意すると、
$\zeta_6^2×\zeta_6^5=\zeta_6$
ですが、$\zeta_6$は$H_1$の元になっていないため、
$H_1$は演算×で閉じていません。
このように、
「$H$は$G$の部分集合」という条件だけでは、
都合よく$H$が群としての構造をもつことはないのです。
なのでまずは、
「$H$が$G$と同じ演算について閉じている」
という条件を付ける必要があります。
それが部分群の条件①です。
① $a, b \in H$ならば、$a〇 b \in H$
↑今回は、演算〇については掛け算×を採用しています。
ではここで、他の例を見てみましょう。
$G_2=\mathbb{Z}$
とします。$\mathbb{Z}$は整数を表しています。
$\mathbb{Z}=\lbrace \cdots -2, -1, 0, 1, 2, \cdots \rbrace$
です。整数は掛け算×については群になりませんが(逆元がないため)
足し算+については群となります。
ここで、$G_2$の部分集合$H_2$を考えましょう。
例えば、
$H_2=\lbrace 2a \mid a=0, 1, 2, 3, \cdots \rbrace $
とします。
(偶数)+(偶数)=(偶数)
ですので、$H_2$は足し算について閉じています。
また、足し算について結合法則が成立することも自明です。
さらに、足し算の単位元である$0$について、
$0 \in H_2$です。
$H_2$は単位元もしっかりもっています。
にも関わらず、$H_2$は足し算+について群になりません。
なぜか?
それは、逆元を持たないからです。
例えば足し算における$2$の逆元は$-2$ですが、
$-2$は$H_2$の元になりません。
ゆえに、
「$H$は$G$と同じ演算について必ず逆元をもつ」
という条件を追加する必要が生じます。
これが部分群の条件②です。
② $a \in H$ならば、$a^{-1} \in H$
あとは、$H$は単位元をもつ、ということを保証できればよさそうですが、
実はこれは条件①と条件②から導くことができるので、
条件を追加して単位元の存在を要求する必要はありません。
そのことを確認しておきましょう。
まず、部分群の条件②より、
$a \in H$なら$a^{-1} \in H$
です。
単位元を$e$で表すことにしましょう。
$e \in H$が確認できればよいです。
ここで、条件①より、
$a, b \in H$ならば$a〇b \in H$
です。$a^{-1} \in H$なので、
$a〇a^{-1} \in H$
でなければなりません。
$a^{-1}$が$a$の逆元であることから、
$a〇a^{-1} =e$
であり、
$a〇a^{-1} \in H$
から
$e \in H$
となります。
あとは$H$が空集合でないことだけ保証できればよく、
それが部分群の条件③となり、追加すべき最後の条件となります。
以上のことから、
「ある群$G$の部分集合$H$もまた群」
という条件を数式に落とし込むと
① $a, b \in H$ならば、$a〇 b \in H$
② $a \in H$ならば、$a^{-1} \in H$
③ $H$は空集合ではない
となり、これが先ほどの見出しで紹介した部分群の定義となります。
おまけ
先ほどの見出しでは部分群とならない例を紹介したので、
最後に部分群の具体例を紹介します。
1の6乗根について
$G=\lbrace \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5, 1 \rbrace$
とします。これは先ほどの見出しで確認した通り、掛け算×について群です。
ここで、
$H= \lbrace \zeta_6^2, \zeta_6^4, 1 \rbrace$
とすると、うまいこと$H$は群としての構造をもちます。
それを演算表で確かめておきましょう。
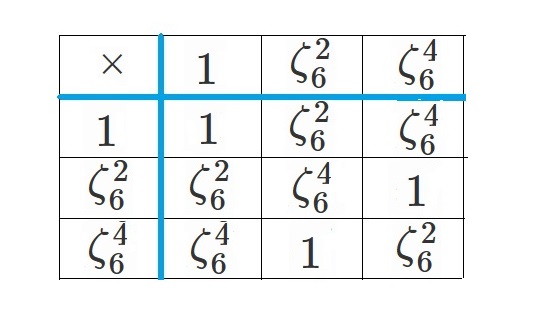
×について閉じていることが確認できるので、
部分群の条件①を満たしていることが分かります。
また、1×1=1なので、1の逆元は1です。
$\zeta_6^2×\zeta_6^4=\zeta_6^4 ×\zeta_6^2=1$
なので、$\zeta_2$の逆元は$\zeta_4$で、
$\zeta_6^4$の逆元は$\zeta_6^2$です。
ちゃんと逆元が存在するので、部分群の条件②もクリアです。
$H$が空集合でないことは自明なので、部分群の条件③もクリアです。
以上のことから、$H$は$G$の部分群であることが確認できます。
3次の対称群について
3つの並べ替え全体の集合$S_3$について考えます。
3!=6通りの元があり、具体的にかきくだすと以下の6つです。

ここで、
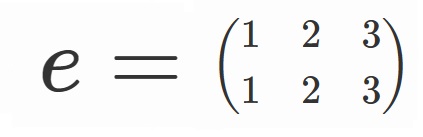
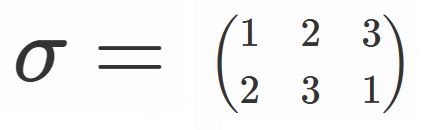
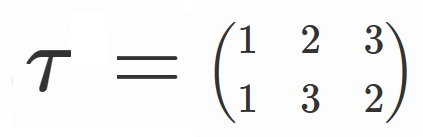
とすると、
$S_3=\lbrace e, \sigma, \sigma^2, \tau, \tau \sigma, \tau \sigma^2 \rbrace$
は以下の演算表より、写像の合成〇について群となります。

ここで、$S_3$の部分集合
$A_3=\lbrace e, \sigma, \sigma^2 \rbrace$
について考えましょう。
まず、$A_3$は〇について閉じています
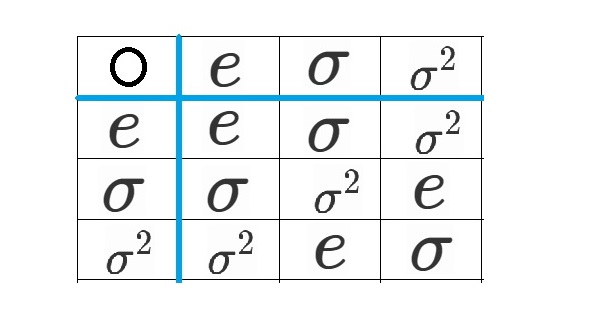
また、$e〇e=e$より、
$e$の逆元は$e$自身です。
$\sigma 〇 \sigma^2 =\sigma^2 〇 \sigma =e$
より、$\sigma$の逆元は$\sigma^2$で、
$\sigma^2$の逆元は$\sigma$です。
$A_3$が空集合でないことは自明なので、
ここまでの議論より、$A_3$は$S_3$の部分集合であることが分かります。
まとめ
いかができたか?
部分群という概念について
・定義
・なぜそんな定義になっているのか
・具体例
についてまとめました。
次回の記事では、部分群によって群をグループ分けする剰余類という考え方を紹介します。
ご期待ください。

コメント