加法定理の証明には様々な別解があります。
今回の主役は余弦定理
証明の発想
三角関数の加法定理。
$\sin (\alpha +\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta$
$\cos (\alpha +\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta$
$\tan (\alpha +\beta)=\dfrac{\tan \alpha +\tan \beta}{1-\tan \alpha \tan \beta}$
前回の記事では、三角比の定義に基づいて
ビッグライトをメインの武器に証明をしました。
しかし、ウルトラマン流の三角比の定義では、
$0<\alpha +\beta <\dfrac{\pi}{2}$
の範囲でしか加法定理を説明できないという弱点があったため、
鈍角の場合でも証明できる手段はないか?
というアプローチが必要でした。
前回の記事はこちらをご覧ください。
そこで、鈍角の場合も上手く扱うために、単位円を召喚します。
ちなみに、単位円によるサイン・コサインの定義についての記事があるので、
よければ参照してください。

単位円上に$\alpha +\beta$をかくと、次のようになります。
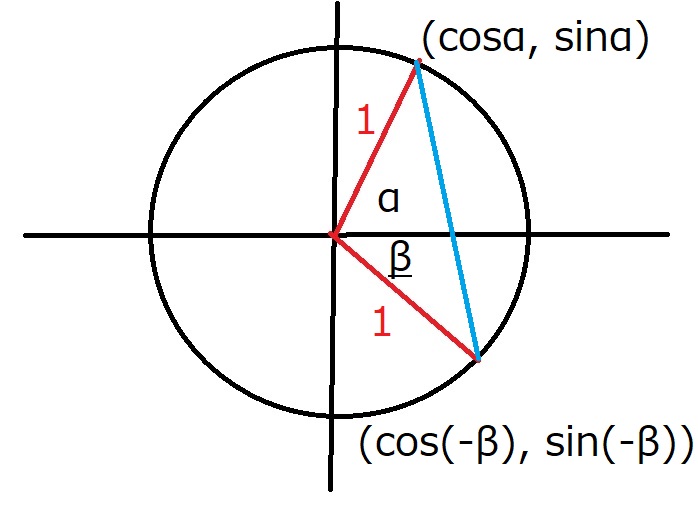
原点を基準に反時計回りに$\alpha$回した点と、
時計回りに$\beta$合した点で$(\alpha +\beta)$を表現する点がポイントです。
さて。
今回は単位円を考えているので、この円の半径は1です。
つまり、図の赤い部分の長さは1です。
図の三角形について、二辺のながさとその間の角の大きさが分かっています。
このような時には、余弦定理が有効です。
(補足)
余弦定理を正弦定理の使い分け
正弦定理→「外接円というキーワードがある」OR「角の条件が多い」
余弦定理→「長さの条件が多い」
角の正弦定理、長さの余弦定理
と覚えておくと使い勝手が良いです。
今回は、長さの条件が多いので、余弦定理です。
また、余弦定理はコサインについての定理なので、
加法定理のコサインの式が先に求まることになります。
証明
(証明)
$\cos (\alpha +\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta$
を示す。
単位円上に2点$A, B$をとり、
$A(\cos \alpha, \sin \alpha), B(\cos (-\beta), \sin (-\beta))とする。$
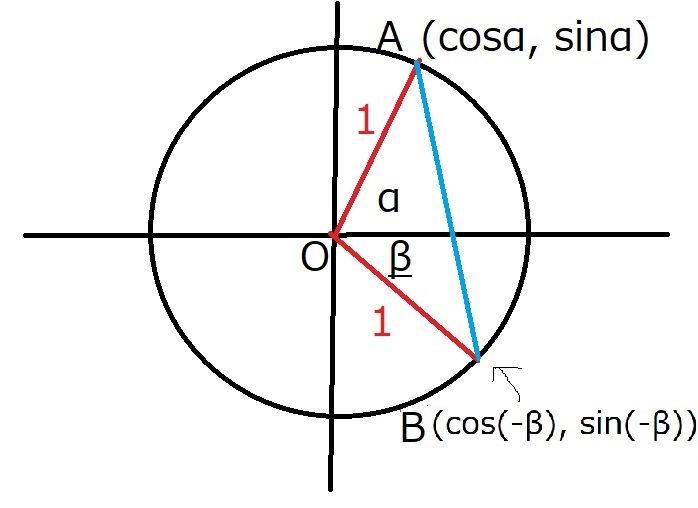
また、原点を$O$とする。
三角形$OAB$について、
$AB=\sqrt{\lbrace \cos (-\beta)-\cos \alpha \rbrace^2+\lbrace \sin(-\beta)-\sin \alpha \rbrace^2}$
である。(2点間の距離の公式)
三角関数の性質より、$\cos (-\beta)=\cos \beta, \sin (-\beta)=-\sin \beta$
に注意すると、
$AB=\sqrt{\lbrace \cos \beta-\cos \alpha \rbrace^2+\lbrace -\sin \beta-\sin \alpha \rbrace^2}$
$AB=\sqrt{\cos^2\beta -2\cos \alpha \cos \beta+\cos^\alpha +\sin^2\beta +2\sin\alpha \sin \beta +\sin^2\alpha}$
$AB=\sqrt{(\cos^2 \beta +\sin^2 \beta)+(\cos^2\alpha +\sin^2\alpha)+2(\sin \alpha \sin \beta -\cos \alpha \cos \beta)}$
ここで、$\sin^2 \theta +\cos^2\theta =1$なので、
$AB=\sqrt{2+2(\sin \alpha \sin \beta -\cos \alpha \cos \beta)}$
となる。
ここで、$⊿OAB$について、余弦定理より、
$AB^2=OA^2+OB^2-2OA・OB\cos (\alpha +\beta)$
である。
これに$AB=\sqrt{2+2(\sin \alpha \sin \beta -\cos \alpha \cos \beta)}, OA=1, OB=1$を代入。
$2+2(\sin \alpha \sin \beta -\cos \alpha \cos \beta)=1+1-2\cos (\alpha +\beta)$
移項して整理すると、
$\cos (\alpha +\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta$
(証明終了)
ついでにサインの場合もやってしまいましょう。
コサインの加法定理をベースに改造していきます。
その際、三角関数の性質の式
$\cos (\theta +\dfrac{\pi}{2})=-\sin \theta$
と
$\sin (\theta +\dfrac{\pi}{2})=\cos \theta$
を使います。
(証明)
$\cos (\alpha +\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta$
を用いて
$\sin (\alpha +\beta)=\sin \alpha \cos \beta +\sin \alpha +\cos \beta$
を示す。三角関数の性質より、
$\cos (\theta +\dfrac{\pi}{2})=-\sin \theta$
となり、
$\sin \theta =-\cos (\theta +\dfrac{\pi}{2})$
である。これに
$\theta =\alpha +\beta$
を代入する。
$\sin (\alpha +\beta)=-\cos (\alpha +\beta +\dfrac{\pi}{2})$
$\sin (\alpha +\beta)=-\cos \lbrace \alpha +(\beta +\dfrac{\pi}{2}) \rbrace$
右辺について、コサインの加法定理より、
$-\cos \lbrace \alpha +(\beta +\dfrac{\pi}{2}) \rbrace=-\lbrace \cos \alpha \cos(\beta +\dfrac{\pi}{2})-\sin \alpha \sin(\beta +\dfrac{\pi}{2})$
$\cos (\theta +\dfrac{\pi}{2})=-\sin \theta$
と
$\sin (\theta +\dfrac{\pi}{2})=\cos \theta$
より、
$-\lbrace \cos \alpha \cos(\beta +\dfrac{\pi}{2})-\sin \alpha \sin(\beta +\dfrac{\pi}{2})\rbrace$
$ = – \cos \alpha (-\sin \beta)+\sin \alpha \cos \beta$
$=\cos \alpha \sin \beta +\sin \alpha \cos \beta$
$=\sin \alpha \cos \beta +\cos \alpha \sin \beta$
よって、
$\sin (\alpha +\beta)=\sin \alpha \cos \beta +\sin \alpha +\cos \beta$
(証明終了)
タンジェントについては前回と全く同じ証明のなので、今回はサボります笑
なお、途中用いた三角関数の性質の公式について気になる方は、
以下の記事をご覧ください、
まとめ
いかがでしたか?
今回は、鈍角の場合も通用する三角関数の加法定理の証明を紹介しました。
主役は余弦定理ですね。
この証明が一番オーソドックスな証明なように感じます。
他にも色々別解はあるので、それはまた気が向いたときに別の記事で紹介しようと思います。
お楽しみに
ではまた次の記事でお会いしましょう!
コメント