群論のピークは準同型定理ですが、
これはまたの名を第一同型定理といいます。
第一があるということは、当然第二と第三もあります。
今回は、第二同型定理について証明を行っていきます!
第2同型定理とは?
(第二同型定理)
$G$を群とし、$H$を$G$の部分群とする。
$N$が$G$の正規部分群であるとき、
$ HN/N \cong H/H \cap N$
が成り立つ。
定理の主張自体は以上なのですが、ちょっと説明不足なところがあるので、
補っていこうと思います。
まず、$HN$ってなんだよ!と思ったことでしょう。
$HN$がどんな集合かというと、
$HN=\lbrace h〇n \mid h \in H, n \in N \rbrace$
です。
単純に$H$の元と$N$の元に対して演算〇を作用させたもの全体の集合が$HN$です。
第二同型定理ですが、イメージ的には、相似っぽいイメージが分かりやすいかと思います。
相似とは、形が同じだけど大きさだけ違う関係を言います。
例えば、のび太君にビッグライトを当てるとでっかくなりますが、
突然のび太君の指が6本になったりはりません。
のび太君はのび太君のまま、大きさだけがでかくなります。
これが相似です。
さて、下のベン図を見てください。
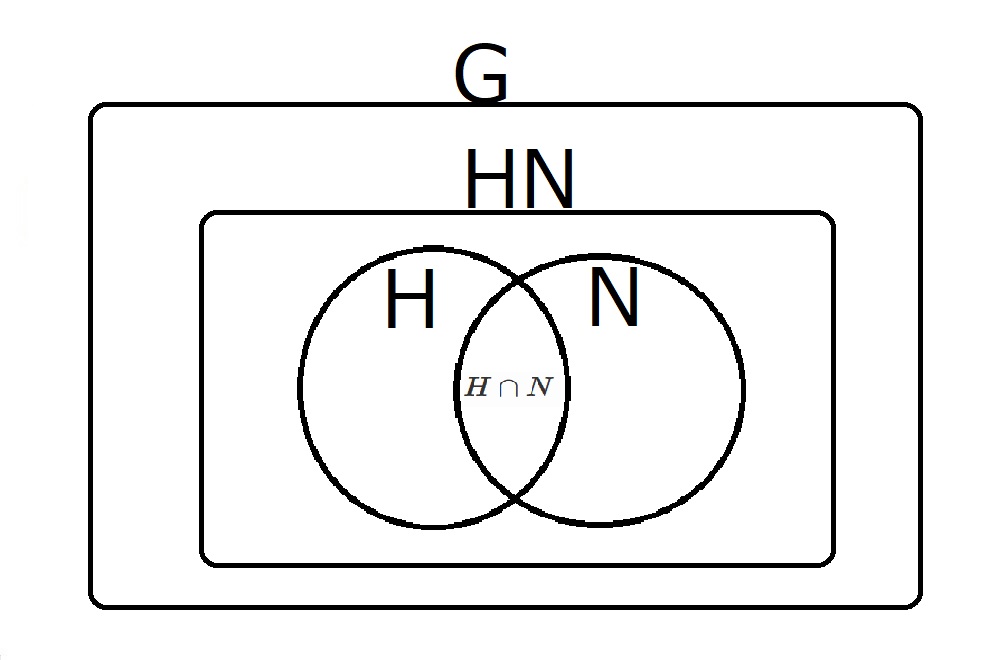
これが第二同型定理のフィールドです。
さて、これを以下のように色分けしてみようと思います。
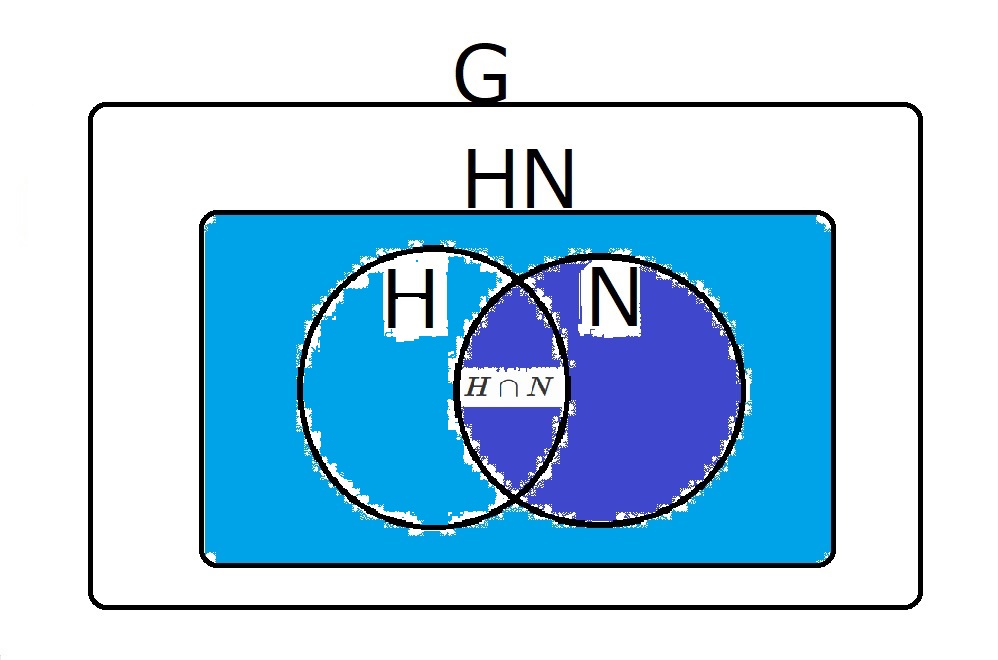
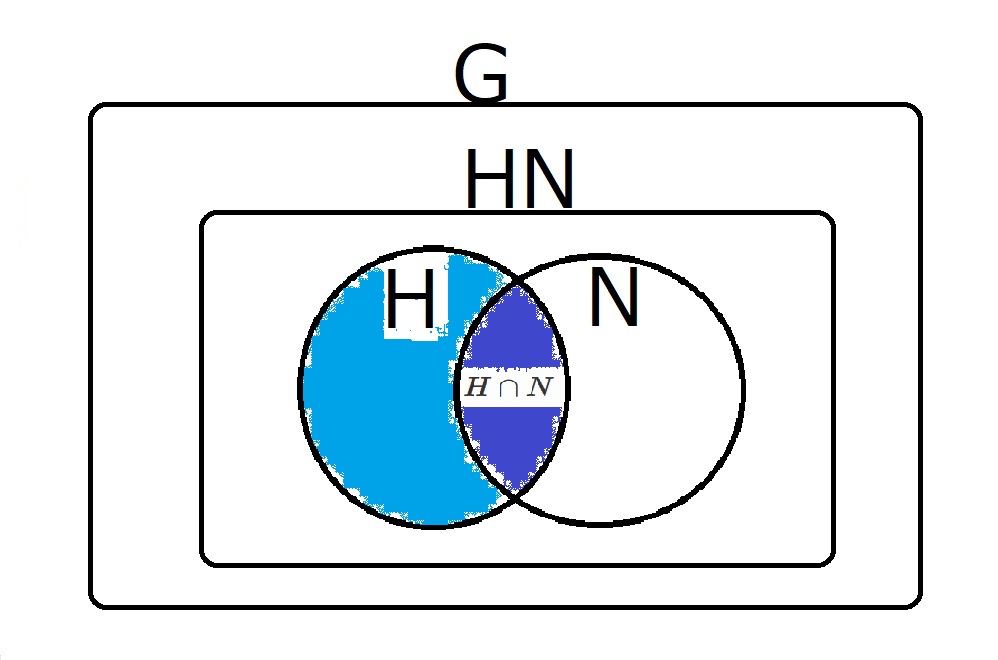
上の図で水色と濃い青で色分けした部分と、
下の図で水色と濃い青で色分けした部分が
相似っぽい関係になっているよ!
というのが第二同型定理のです。
$ HN/N \cong H/H \cap N$
だけ見るとなんだかイメージが沸きずらいと思いますが、
あぁ要するにこれは、
広い集合の割り算と、狭い集合の割り算が同じような構造を持っていて、
相似っぽい感じだと言っているだけなんだ!
と思えば多少親しみやすくなると思います。
そして、広いのと狭いのが同じ構造を持っているなら、当然狭い方が調べやすいです。
狭きを調べて広きを知ることができる、という点が第二同型定理の偉い所です。
では、次は具体例を考えていきましょう!
第二同型定理を考えていくにあたっては、
・剰余類・剰余群
・正規部分群
・準同型写像
・像と核
・準同型定理
についての知識が必要となるので、これらに馴染みにない方は以下の記事をご覧ください。
剰余類・剰余群について

正規部分群について

準同型写像について

像と核について

準同型定理(第一同型定理)について
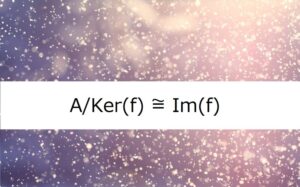
第二同型定理の具体例
では、ここから第二同型定理の具体例を見ていきましょう。
(第二同型定理)
$G$を群とし、$H$を$G$の部分群とする。
$N$が$G$の正規部分群であるとき、
$ HN/N \cong H/H \cap N$
が成り立つ。
$G=\mathbb{Z}$とし、
$H=12\mathbb{Z}$とし、
$N=18\mathbb{Z}$としましょう。
$\mathbb{Z}$は整数全体の集合です。
これを足し算+についての群と解釈しましょう。
$12\mathbb{Z}$は、要するに12の倍数全体を表していて、
$18\mathbb{Z}$は18の倍数全体を表しています。
$H \cap N=(12\mathbb{Z}) \cap (18 \mathbb{Z})$
ですので、$H \cap N$は
12の倍数かつ18の倍数であるもの全体でできた集合です。
12と18の最小公倍数は36なので、
$H\cap N=36 \mathbb{Z}$となります。
さて、次に$HN$を考えていきますが、ここは勘違いが起きやすいので(大学生の時の僕)、
少し慎重に考えていきましょう。
$HN=\lbrace h〇n \mid h \in H, n \in N \rbrace$
でした。いま、
$H=12\mathbb{Z}$と$N=18\mathbb{Z}$は
ともに足し算+についての群です。
ゆえに、今回は演算〇は、+となります。
掛け算ではないので気を付けましょう。
$HN=\lbrace h〇n \mid h \in H, n \in N \rbrace$
$=\lbrace h+n \mid h \in 12\mathbb{Z}, n \in 18\mathbb{Z} \rbrace $
です。ここで、
$h \in 12\mathbb{Z}$から、$h=12s$となる整数$s$が存在します。
同様に、$n=18t$となる整数$t$が存在します。
よって、
$HN=\lbrace 12s+18t \mid s, t \in \mathbb{Z} \rbrace$
となります。
$12s+18t=6(2s+3t)$
であり、$2s+3t \in \mathbb{Z}$です。
したがって、
$HN=\lbrace 6u \mid u \in \mathbb{Z} \rbrace$
$=6\mathbb{Z}$
となります。
ここで、
$HN/N$ と $ H/H \cap N$
を考えましょう
まずは$HN/N$から。
$HN/N=6\mathbb{Z}/18\mathbb{Z}$
$=\lbrace x+18\mathbb{Z} \mid x \in 6\mathbb{Z} \rbrace$
となります。
$x \in 6\mathbb{Z}$なので、
$x=6y$となる$y \in \mathbb{Z}$が存在します。
よって、
$HN/N=6\mathbb{Z}/18\mathbb{Z}$
$=\lbrace 6y +18\mathbb{Z} \mid y \in \mathbb{Z} \rbrace$
$=\lbrace \cdots, 6+18\mathbb{Z}, 12+\mathbb{Z}, $
$18+18\mathbb{Z}, 24+18\mathbb{Z}, \cdots, \rbrace$
となります。ここで、
$6+18\mathbb{Z}$と$24+18\mathbb{Z}$を考えましょう。
6を18で割った余りは6です。
24を18で割った余りも6です。
ゆえに、$6+18\mathbb{Z}=24+18\mathbb{Z}$となります。
同様に、
$12+18\mathbb{Z}=30+18\mathbb{Z}$
$0+18\mathbb{Z}=18+18\mathbb{Z}=36+18\mathbb{Z}$
が成り立ちます。
したがって、
$HN/N=6\mathbb{Z}/18\mathbb{Z}$
$=\lbrace 0+18\mathbb{Z}, 6+18\mathbb{Z}, 12+18\mathbb{Z} \rbrace$
となります。
次に $H/H \cap N$を考えましょう。
$H/H \cap N=12\mathbb{Z}/ \lbrace (12+\mathbb{Z}) \cap (18+\mathbb{Z})\rbrace$
$=12\mathbb{Z}/36\mathbb{Z}$
$=\lbrace 12k +36\mathbb{Z} \mid k \in \mathbb{Z}\rbrace $
$=\lbrace 0+36\mathbb{Z}, 12+36\mathbb{Z}, 24+36\mathbb{Z}\rbrace $
さて。
$HN/N=\lbrace 0+18\mathbb{Z}, 6+18\mathbb{Z}, 12+18\mathbb{Z} \rbrace$
$H/H \cap N=\lbrace 0+36\mathbb{Z}, 12+36\mathbb{Z}, 24+36\mathbb{Z}\rbrace$
です。
この2つは同型でしょうか? 同型ではないでしょうか?
同型か同型でないかは、同型写像が作れるかどうかが運命の分かれ道でした。
演算表を見てみましょう
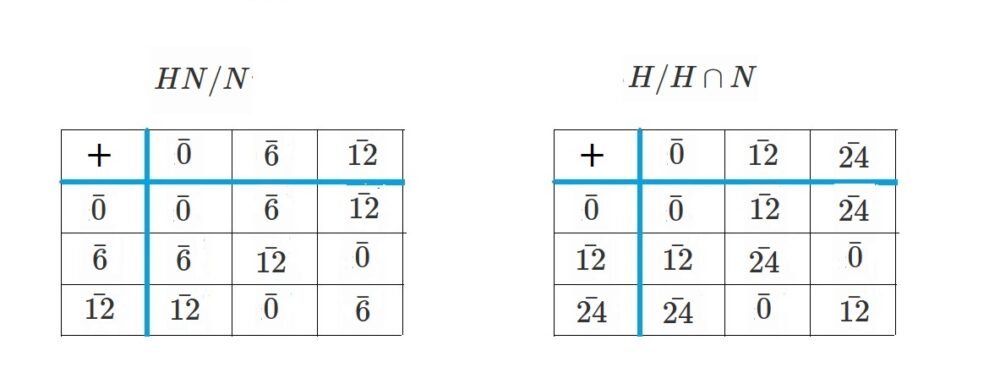
同型っぽいですね!
$HN/N$から$H/H\cap N$への写像として、
$f(n+18\mathbb{Z})=2n+36\mathbb{Z}$
というものを定めるとよさそうです。
以上のことから、確かに
$ HN/N \cong H/H \cap N$
は成り立っていそうです。
次の見出しでは、いよいよ第二同型定理を証明していきます。
第二同型定理を示すための補題たち
今一度、第二同型定理の内容を確認しておきましょう。
(第二同型定理)
$G$を群とし、$H$を$G$の部分群とする。
$N$が$G$の正規部分群であるとき、
$ HN/N \cong H/H \cap N$
が成り立つ。
$ HN/N \cong H/H \cap N$に着目しましょう。
これは、$HN/N$と$H/H \cap N$が群として同型であることを示しています。
まずここが突っ込みポイントです。
$HN/N$と$H/H \cap N$って、そもそも群なの?
剰余類っていつも群になるとは限らないけど!!
そう。
剰余類が群になるためには、正規部分群という条件が必要です。
そこで、まずは補題として以下を確認しておかなければなりません。
・$H \cap N$は$G$の部分群である
・$HN$は$G$の部分群である
・$N$は$HN$の正規部分群である
・$H \cap N$は$H$の正規部分群である
(第二同型定理の補題①)
$G$を群とし、$H$と$N$を$G$の部分群とする。
このとき、$H \cap N$は$G$の部分群となる。
部分群であることを示すには、
①演算が閉じていること
②逆元があること
③空集合でないこと
を示せばよいのでした。
詳しくは以下の記事をご覧ください。

(第二同型定理の補題①の証明)
$G$を演算〇についての群とし、$e$を$G$の単位元とする。
$H \cap N$について考える。
$H$は$G$の部分群であるので、$e \in H$でなければならない。
$N$も$G$の部分群であるので、同様に$e \in N$でなければならない。
よって、$e \in H \cap N$となり、
$H \cap N$は空集合にはなりえない…①
ここで、$a, b \in H \cap N $について、
$a〇b \in H \cap N$であることを示す。
$H \cap N$の定義より、
$a, b \in H$かつ$a, b \in N$である。
いま、$H$は$G$の部分群であるので、
$a〇b \in H$でなければならない。
また、$N$も$G$の部分群であるので、$a〇b \in N$でなければならい
$a〇b \in H$かつ$a〇b \in N$であるので、
$a〇b \in H\cap N$である…②
最後に、$a \in H \cap N$のとき、
$a^{-1} \in H \cap N$であることを示す。
$a \in H \cap N$より、
$a \in H$かつ$a \in N$である。
$H$は$G$の部分群より、$a^{-1} \in H$であり、
$N$も$G$の部分群より、$a^{-1} \in N$である。
$a^{-1} \in H$かつ$a^{-1} \in N$より、
$a^{-1} \in H \cap N$である…③
①②③より、$H \cap N$は$G$の部分群である。
(証明終了)
続いて補題②です
(第二同型定理の補題②)
$G$を群とし、$H$と$N$を$G$の部分群とする。
このとき、特に$N$が$G$の正規部分群であるならば、
$HN$は$G$の部分群となる。
注目すべきは、$N$が正規部分群である、という条件です。
$HN=\lbrace hn \mid h \in H, n\in N \rbrace$
はいつでも群になるわけではないということを覚えておきましょう。
(第二同型定理の補題②の証明)
$G$を演算〇についての群とし、$e$を$G$の単位元とする。
$H$は$G$の部分群より、$e \in H$であり、
$N$も$G$の部分群なので、$e \in N$である。
いま、$HN$について、定義より
$HN=\lbrace h〇n \mid h \in H, n\in N \rbrace$
である。
$e \in H$と$e \in N$より、$e〇e \in HN$となるため、
$HN$は空集合ではない…①
次に$a, b \in HN$であるときに
$a〇b \in HN$であることを示す。
$a \in HN$より、$a=h_1〇n_1$となる
$h_1 \in H$と$n_1 \in N$が存在する。
どうように、$b \in HN$より、
$b=h_2〇n_2$となる
$h_2 \in H$と$n_2 \in N$が存在する。
$(h_1〇n_1)〇(h_2〇n_2) \in HN$を示せばよい。
いま、$H$と$N$は$G$の部分群であるので、
結合法則より、
$(h_1〇n_1)〇(h_2〇n_2)=h_1〇n_1〇h_2〇n_2$
である。
ここで、$N$が$G$の正規部分群であることより、
$g \in G$に対して
$g〇N=N〇g$
が成り立つ。$g=h_2$とすると、
$h_2〇N=N〇h_2$である。
よって、$h_2〇n_1=n_1〇h_2$が成り立つ。
ここで、
$(h_1〇n_1)〇(h_2〇n_2)=h_1〇n_1〇h_2〇n_2$
と$h_2〇n_1=n_1〇h_2$より、
$(h_1〇n_1)〇(h_2〇n_2)=h_1〇n_1〇h_2〇n_2$
$=h_1〇h_2〇n_1〇n_2$
$=(h_1〇h_2)〇(n_1〇n_2)$
となる。$H$は$G$の部分群より、
$h_1〇h_2 \in H$であり、同様に
$n_1〇n_2 \in N$である。
したがって、
$(h_1〇h_2)〇(n_1〇n_2) \in HN$となり、
$a〇b \in HN$である…②
最後に$c \in HN$のとき、$c^{-1} \in HN$を示す。
$c \in HN$より、$c=h_3〇n_3$となる
$h_3 \in H$と$n_3 \in N$が存在する。
$H$は$G$の部分群より、$h_3^{-1} \in H$であり、
同様に$n_3^{-1} \in N$である。
$c^{-1}=x$とすると、逆元の定義より
$c〇x=x〇c=e$である。
$c〇x=e$に着目する。
$(h_3〇n_3)〇x=e$である。
結合法則より、
$h_3〇n_3〇x=e$
両辺に$h_3^{-1}$を左から合成すると、
$h_3^{-1}〇h_3〇n_3〇x=h_3^{-1}〇e$
$n_3〇x=h_3^{-1}$
両辺に$n_3^{-1}$を左から合成すると、
$n_3^{-1}〇n_3〇x=n_3^{-1}〇h_3^{-1}$
$x=n_3^{-1}〇h_3^{-1}$
である。よって、
$c=h_3〇n_3$であるときに
$n_3^{-1}〇h_3^{-1} \in HN$を示せばよい。
ここで、$N$は$G$の正規部分群より、
$g \in G$に対して
$g〇N=N〇g$
である。
$g=h_3^{-1}$とすると、
$h_3^{-1}〇N=N〇h_3^{-1}$
となるため、
$h_3^{-1}〇n_3^{-1}=n_3^{-1}〇h_3^{-1}$
となる。
$HN=\lbrace h〇n \mid h \in H, n \in N \rbrace $
であったので、
$h_3^{-1} 〇n_3^{-1} \in HN$
である。
$h_3^{-1}〇n_3^{-1}=n_3^{-1}〇h_3^{-1}$
より、
$n^{-1}〇h_3^{-1} \in HN$
となり、$c^{-1} \in HN$である…③
①②③より、$HN$は$G$の部分群である。
(証明終了)
続いて補題③です!
(第二同型定理のの補題③)
$G$を群とし、$H$を$G$の部分群とする。
$N$は$G$の正規部分群である。
このとき、$N$は$HN$の正規部分群となる。
(第二同型定理の補題③の証明)
$N$が$HN$の正規部分群であることを示す。
$x \in HN$に対して、$x〇N=N〇x$であればよい。
条件より、$N$は$G$の正規部分群であるので、
$g \in G$に対して$g〇N=N〇g$である。
いま、第二同型定理の補題②より、
$NH$は$G$の部分群である。
したがって、$x \in HN$であるならば$x \in G$
である。
$g〇N=N〇g$について、$g=x$
とすると、
$x〇N=N〇x$
となり、
$N$は$HN$の正規部分群となる。
(証明終了)
ラストは補題④です!
(第二同型定理の補題④)
$G$を群とし、$H$を$G$の部分群とする。
$N$は$G$の正規部分群である。
このとき、$H \cap N$は$H$の正規部分群となる。
正規部分群の定義を思い出しておきましょう。
$H \cap N$が$H$の正規部分群であることを示すには、
$h〇(H\cap N)=(H\cap N)〇h$を示せばよいですが、これと同値な表現として
$h〇(H\cap N)〇h^{-1}=H \cap N$を示してもよいです。
今回は後者を採用していこうと思います。
(第二同型定理の補題④の証明)
$H \cap N$が$H$の部分群であることを示す。
そのために、$h \in H$と$x \in H\cap N$について
$h〇x〇h^{-1}\in H\cap N$を示す。
つまりは$h〇x〇h^{-1}\in H$かつ$h〇x〇h^{-1}\in N$であればよい。
$x \in H\cap N$より、$x \in H$である。
$H$は$G$の部分群より、
$h〇x〇h^{-1}\in H$である…①
ここで、$N$は$G$の正規部分群であるので、
$g \in G$について$g〇N=N〇g$である。
$H$は$G$の部分群より、$h \in G$である。
$g=h$とすると、
$h〇N=N〇h$である。
よって、$h〇N〇h^{-1}=N$となり、
$h〇x〇h^{-1}\in N$である…②
①②より、$h〇x〇h^{-1}\in H\cap N$となり、
$H \cap N$は$H$の正規部分群である。
(証明終了)
第二同型定理の証明
さて、いよいよ第二同型定理の証明です!
(第二同型定理)
$G$を群とし、$H$を$G$の部分群とする。
$N$が$G$の正規部分群であるとき、
$ HN/N \cong H/H \cap N$
が成り立つ。
はい。今回は同型を示す証明です。
しかも、剰余群の同型を示す証明です!
剰余群+同型=準同型定理の利用
という発想で証明を組み立てていきましょう!
(準同型定理)
群$A$から群$B$への準同型写像を$f$とする。
このとき、$A/Ker(f) \cong Im(f)$
が成り立つ。
また、像と核の定義もおさらいしておきます。
(像の定義)
群$A$から群$B$への準同型写像を$f$とする。
このとき、
$\lbrace f(a) \mid a \in A \rbrace$
を$f$の像といい、
$Im(f)=\lbrace f(a) \mid a \in A \rbrace$
で表す
(核の定義)
群$A$から群$B$への準同型写像を$f$とする。
また、$B$の単位元を$e_b$とする
このとき、
$\lbrace a \in A \mid f(a)=e_b \rbrace$
を$f$の核といい、
$Ker(f)=\lbrace a \in A \mid f(a)=e_b \rbrace$
で表す。
準同型定理の使いかたとしては、
①群$A$から群$B$への準同型写像$f$を自分で定める
②すると自動的に$A/Ker(f) \cong Im(f)$という同型をゲットできる
という流れになります。
今回示したいのは
$ HN/N \cong H/H \cap N$
です。
まず、何を$A, B$とし、どうやって準同型写像$f$を定めるかという点が大切です。
結論から述べると、$A=H, B=G/N$と定めると上手くいきます。
(第二同型定理の証明)
$G$を演算〇についての群とし、$H$を$G$の部分群とする。
$N$が$G$の正規部分群であるとき、
$ HN/N \cong H/H \cap N$
であることを示す。
$H$から$G/N$への写像$f$を次のように定める。
$f(h)=h〇N$ (ただし、$h\in H$)
すると、$f$は準同型写像となる。
準同型定理を使いたいので、$Im(f)$を考える。
$Im(f)= \lbrace f(h) \mid h \in H \rbrace$
より、
$Im(f)= \lbrace h〇N \mid h \in H \rbrace$
ここで、$n \in N$を任意に定めると、
$n〇N=N$であるので、
$Im(f)= \lbrace h〇N \mid h \in H \rbrace$
$=\lbrace h〇(n〇N) \mid h \in H , n \in N\rbrace$
$= \lbrace (h〇n)〇N \mid h \in H, n \in N \rbrace$
$=HN/N$
である。
よって、$Im(f)=HN/N$…①
次に$Ker(f)$を考える。
$HN/N$の単位元が$N$であることを踏まえると、
$Ker(f)=\lbrace h \in H \mid f(h)=N \rbrace$
である。
$f(h)=N$を満たす$h$について考える。
$f(h)=h〇N$
であったので、
$h〇N=N$
である。これが成立するには、$h \in N$でなければならない。
したがって、$h \in H$かつ$h \in N$
から、$h \in H\cap N$である。
よって、
$Ker(f)=H\cap N$である…②
ここで、準同型写像$f$に対して、
準同型定理より、
$H/Ker(f) \cong Im(f)$…③
であった。
①②より、
$Im(f)=HN/N$
$Ker(f)=H \cap N$
であったので、③にこれらを代入すると、
$H/H \cap N \cong HN/N$
となる。
(証明終了)
まとめ
いかがでしたか?
・第二同型定理の主張は$H/H \cap N \cong HN/N$
・これは相似っぽいイメージで理解する
・狭きを調べて広きを知ることができる点が第二同型定理の利点
・第二同型定理の証明は、剰余群と同型が絡むので、準同型定理が有効
以上の流れを押さえていただければと思います。
次回は第三同型定理(めっちゃ美しい)を扱いますので、ご期待ください。
ではまた次回の記事でお会いしましょう!
参考
画像素材提供(アイキャッチ):Gerd AltmannによるPixabayからの画像

コメント