群論や線形代数をやっていると、いずれ出会うのが「像」と「核」です。
今回は、群における「像」と「核」を考える意味を具体例とともに分かりやすく解説していきたいと思います。
我々は「像」と「核」を何のために学ぶのでしょう?
端的に言えば、それは準同型写像が全射なのか単射なのかのチェックするためです。
群準同型の像について
像は比較的考えやすい概念です。
高校の数学Ⅰで関数を習うとき、
$y=f(x)$
という表し方を見たことがあると思います。
像は、$y=f(x)$の一般化だと思ってください。
今回は群について考えるので、$f$は準同型写像としましょう。
準同型について馴染みのない方は以下の記事をご覧ください。

像の定義
では、像の定義を紹介します。
(像の定義)
群$A$から群$B$への準同型写像を$f$とする。
このとき、
$\lbrace f(a) \mid a \in A \rbrace$
を$f$の像といい、
$Im(f)=\lbrace f(a) \mid a \in A \rbrace$
で表す
図で表すとこんなイメージです。
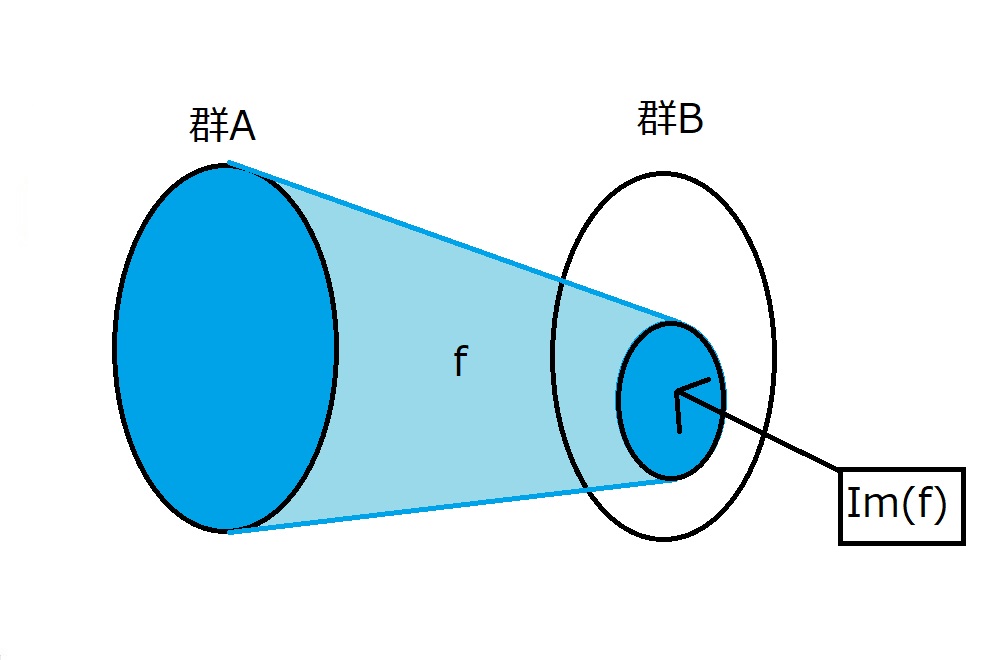
とくに、$Im(f)=B$のときは、下の図のようになります。
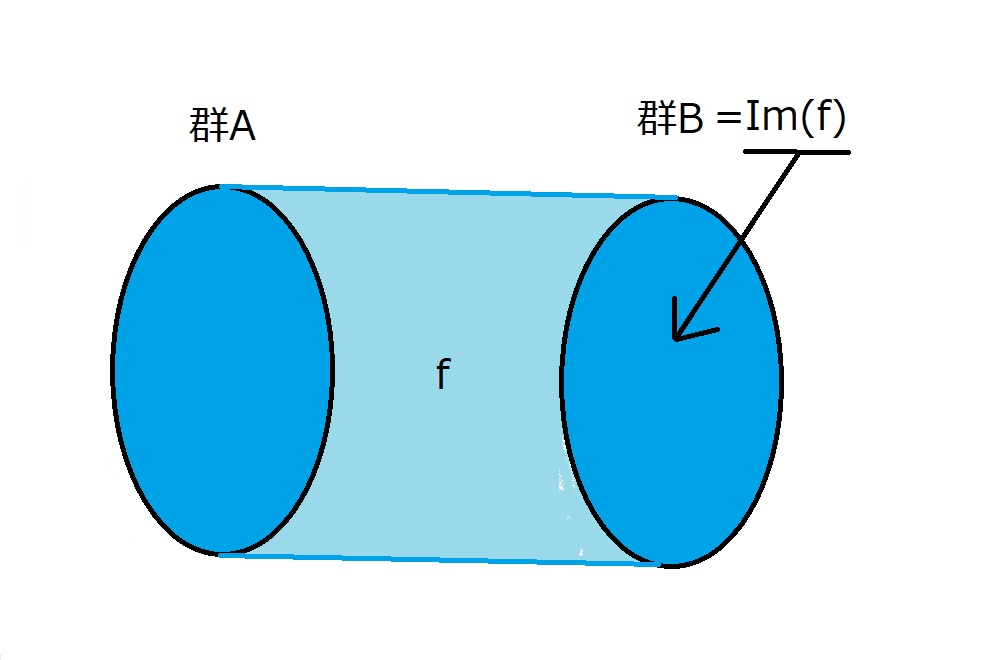
これが意味することは、$f$が全射であるということです。
すなわち、
$Im(f)=B$なら、$f$は全射である
ということです。
これめちゃくちゃ大切なことなので、ぜひ頭の中にとどめておいてください。
像$Im(f)$は、$f$が全射であるかどうかの判定に使えるのです!
あと、余談ですが、$Im(f)$は「イメージ・エフ」と読みます。
全射に馴染みのない方はぜひ以下の記事をご覧ください。

像の具体例
数学的対象は、何事も具体例がないと理解しずらいものです。
ここでは、像の具体例を観察していきましょう。
まず実数$\mathbb{R}$から0を除いた集合$\mathbb{R}^{×}$について考えます。
$\mathbb{R}^{×}$は掛け算について群です。
そして、$X=\lbrace x \mid x \in \mathbb{R}^{×}, x>0 \rbrace$
とします。$X$も掛け算について群となります。
ここで、$\mathbb{R}^{×}$から$X$への写像$f$を
$f(x)=\mid x\mid $
としましょう。
すると、
$f(x×y)=\mid xy \mid$
$ =\mid x \mid ×\mid y \mid $
$=f(x)×f(y)$
となり、$f$は準同型写像であることが分かります。
ここで、$Im(f)$を考えましょう。像の定義より、
$Im(f)=\lbrace f(a) \mid a \in \mathbb{R}^{×} \rbrace$
です。
ここで、$f$の定義から$f(a)=\mid a \mid$です。
で、$a \in \mathbb{R}^{×}$なので、$a$は0ではありません。
ということは、$\mid a \mid >0$
です。
したがって、$Im(f)= \mathbb{R}^{×}$
ということが分かり、$f$は全射ということが分かります。
まぁ今回の例なら、
わざわざ像を使わなくても$f$が全射であることは直観的に十分納得できると思いますが、
$f$が複雑な写像の場合は直観では限界があります。
そんな時、像を使って全射性の確認ができると結構嬉しいのです!
像の性質
像の性質として絶対に抑えておきたいのは、
先ほどの例で確認した全射との関係です。
(像の性質① 全射の判定)
$f$を群$A$から群$B$への準同型写像とする。
$f$が全射であるための必要十分条件は
$Im(f)=B$である。
なぜこれが成り立つかはさきほどの図で納得しておきましょう。
これがシンプルでかつ一番わかりやすいです。

さて、像という概念は$f$全射であるかどうかの判定できるという点で便利ですが、
他にも性質があります。

像のイメージ図から分かるように、
$Im(f) \subset B$
です。
そして、これはただ部分集合であるというだけにとどまりません。
実は、$Im(f)$ は $B$ の部分群になっています。
群としての構造が保たれるのです
それを証明しておきましょう。
(像の性質② 部分群)
$f$を群$A$から群$B$への準同型写像とする。
このとき、$f$の像 $Im(f)$ は$B$の部分群となる。
では、証明をしていきますが、その前に方針の確認です。
まず、$f$は準同型という条件が付いているので、間違いなく
$f(ab)=f(a)f(b)$
は使うことでしょう。
そして、部分群であることを示すには、
部分群の条件3つを確認すればよいです。
具体的には、
① 演算が閉じていること
② 逆元があること
③ 空集合ではないこと
の3つです。
部分群に馴染みのない方は、以下の記事をご覧ください。

では、証明をしていきます。
証明に際しては、
準同型写像の逆元についての性質を使います。
(逆元についての準同型写像の性質)
$f$を群$A$から群$B$への準同型写像とする。
このとき、$A$の任意の元$a$について、
$f(a^{-1})=f(a)^{-1}$
が成り立つ。
逆元についての準同型写像の性質の証明は、
以下の記事をご覧ください。

(像が部分群であることの証明)
演算$*$についての群$A$と、演算$〇$についての群$B$を考える。
$f$を群$A$から群$B$への準同型写像とする。
このとき、$f$の像 $Im(f)=\lbrace f(a) \mid a \in A \rbrace$
が$B$の部分群となることを示す。
そのために、まず$Im(f)$が空集合でないことを確認する。
$ a \in A⇒ f(a) \in B$
であるので、$Im(f)$は空集合ではない…①
次に、$Im(f)$が演算$〇$について閉じていることを示す。
$f(a), f(b) \in Im(f)$を任意にとったとき、
$f(a)〇f(b) \in Im(f)$であればよい。
$A$は群であるので、$a, b \in A ⇒ a*b \in A$である。
$a*b \in A ⇒f(a*b) \in B$
である。
ここで、$f$は準同型写像なので、
$f(a*b)=f(a)〇f(b)$が成立する。
したがって、$f(a)〇f(b) \in Im(f)$である…②
最後に、$f(a) \in Im(f)$を任意にとったとき、
$f(a)^{-1} \in Im(f)$であることを確認する。
いま、$A$は群であるので、
$a \in A$であれば$a^{-1} \in A$である。
そして$a^{-1} \in A$であれば$f(a^{-1}) \in Im(f)$
である。
ここで、逆元についての準同型写像の性質より、
$f(a^{-1})=f(a)^{-1}$
であったので、
$f(a)^{-1} \in Im(f)$である…③
①②③より、$Im(f)$は$B$の部分群である。
(証明終了)
群準同型の核について
先ほどは、$y=f(x)$の一般化という視点で$Im(f)$という概念を定義しました。
これの発想としては、
群$A$の元を$f$で飛ばすと群$B$のどのあたりに飛んでいくかな?
という発想です。
核はこれと逆の発想をします。
すなわち、
群Bの元があったときに、これにとんでくるAの元はどんなのがいるかな?
という発想です。
特に、群Bの単位元に飛んでくる$A$の元を集めた集合を、
$f$の核といいます。
核の定義
では、核の定義を述べていきましょう!
(核の定義)
群$A$から群$B$への準同型写像を$f$とする。
また、$B$の単位元を$e_b$とする。
このとき、
$\lbrace a \in A \mid f(a)=e_b \rbrace$
を$f$の核といい、
$Ker(f)=\lbrace a \in A \mid f(a)=e_b \rbrace$
で表す。
図で表すとこんなイメージです。
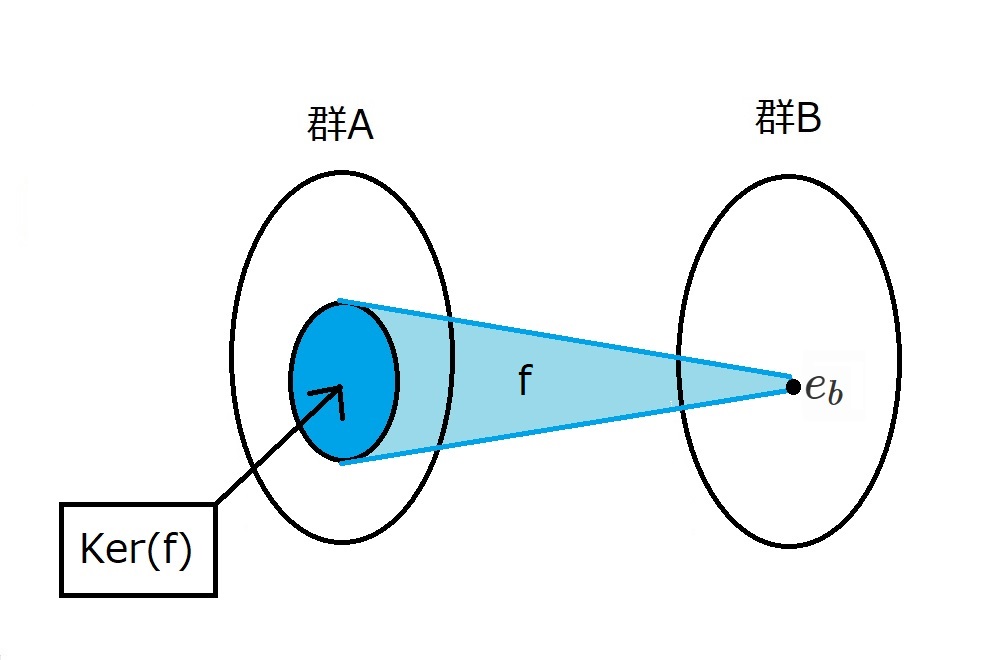
$Ker(f)$は「カーネル・エフ」と読みます。
核の具体例
続いては具体例です
例えば、
$\mathbb{R}^{×}$と
$X=\lbrace x \mid x \in \mathbb{R}^{×}, x>0 \rbrace$
をとって、$\mathbb{R}^{×}$から$X$への写像$f$
を$f(x)=\mid x \mid$
とします。おなじみの例ですね。
ここで核について考えましょう。
$X$の掛け算についての単位元は、もちろん1です。
定義より、
$Ker(f)=\lbrace a \in \mathbb{R}^{×} \mid f(a)=1 \rbrace$
となります。
ここで、$f(a)=\mid a \mid$
でした。
よって、$f(a)=1$を考えると、
$\mid a \mid =1$
です。これを解くと、
$a=1, -1$
となります。したがって、今回は
$Ker(f)=\lbrace 1, -1 \rbrace$
となります。
核の性質
さぁ、ここからが大切です。
核って、一体何の役に立つのでしょうか?
これ、めっちゃ面白いですよ。
実は像と核は対比の関係になっているのです!
どういうことか?
像は、$f$が全射であるかどうか判定できる点が便利なのでした。
核は、$f$が単射であるかどうか判定することができるのです!!!
(核の性質① 単射の判定)
$f$を群$A$から群$B$への準同型写像とする。
また、$A$の単位元を$e_a$とし、$B$の単位元を$e_b$とする。
このとき、$f$が単射となるための必要十分条件は、
$Ker(f)=\lbrace e_a \rbrace$である。
要するに、
$f$が単射 $⇔$ $Ker(f)=\lbrace e_a \rbrace$
ということを主張しています。
これの証明ですが、必要十分条件であることを示すので、
$f$が単射 $⇒$ $Ker(f)=\lbrace e_a \rbrace$
と
$Ker(f)=\lbrace e_a \rbrace$ $⇒$ $f$が単射
を示せばよいことになります。
ここで、単射とは何だったか?
$f$が単射であることはどうやって示せばよかったかというと、
$f(x)=f(y)$ $⇒$ $x=y$
を示せばよいのでした。
単射に馴染みのない方は、こちらの記事をご覧ください。

では証明を進めていきましょう!
(核の性質① 単射の判定の証明)
$A$を演算$*$についての群、$B$を演算$〇$についての群とする。
$f$は群$A$から群$B$への準同型写像である。
また、$A$の単位元は$e_a$であり、$B$の単位元は$e_b$である。
まずは
$f$が単射 $⇒$ $Ker(f)=\lbrace e_a \rbrace$
を示す。
核の定義より、
$Ker(f)=\lbrace a \in A \mid f(a)=e_b \rbrace$
である。
$Ker(f)=\lbrace e_a \rbrace$
を示すためには、$a=e_a$を示せればよい。
いま、$a$について、 $f(a)=e_b$
である。$f$は$A$から$B$への写像なので、
$f(a) \in B$
である。
$B$は群なので、必ず逆元をもつ。
したがって、$f(a)^{-1} \in B$である。
$f(a)=e_b$
の両辺に$f(a)^{-1}$を右から合成する。
$f(a)〇f(a)^{-1}=e_b 〇 f(a)^{-1}$
である。よって、
$e_b=e_b 〇 f(a)^{-1}$
となる。
ここで、逆元についての準同型写像の性質より、
$f(a)^{-1}=f(a^{-1})$
であるので、
$e_b=e_b 〇 f(a^{-1})$
である。
ここで、左辺に$e_b=f(a)$を代入すると、
$e_b=f(a)〇 f(a^{-1})$
となる。
$f$は準同型写像なので、
$f(a)〇f(a)^{-1}=f(a 〇 a^{-1})$
$=f(e_a)$
である。
よって、
$f(e_a)=e_b$
が成り立つ。
もともと
$f(a)=e_b$であったことを踏まえると、
$f(e_a)=f(a)$
である。$f$は単射であったので、
$f(e_a)=f(a)$ $⇒$ $e_a=a$
である。よって、
$f$が単射 $⇒$ $Ker(f)=\lbrace e_a \rbrace$
である…①
次に
$Ker(f)=\lbrace e_a \rbrace$ $⇒$ $f$が単射
を示す。
$x, y \in A$を任意にとり、
$f(x)=f(y)$が成り立つときに$x=y$であることを示せればよい。
$f$は$A$から$B$への写像であるので、
$f(x) \in B$
である。
$B$は群であり、逆元を持つので、$f(x)^{-1} \in B$
である。これを$f(x)=f(y)$に右から合成すると、
$f(x) 〇 f(x)^{-1}=f(y)〇f(x)^{-1}$
となる。
$f(x) 〇 f(x)^{-1}=e_b$であるので、
$e_b=f(y)〇f(x)^{-1}$
である。
ここで、逆元についての準同型写像の性質より、
$f(x)^{-1}=f(x^{-1})$であったので、
$e_b=f(y)〇f(x^{-1})$
である。
$f$は準同型写像なので、
$f(y)〇f(x^{-1})=f(y*x^{-1})$
であり、
$f(y*x^{-1})=e_b$
である。
ここで、$Ker(f)=\lbrace e_a \rbrace$
であったので、
任意の$A$の元$a$について、$f(a)=e_b$であるならば必ず$a=e_a$でなければならない。
したがって、$f(y*x^{-1})=e_b$より、
$y*x^{-1}=e_a$
である。
この両辺に$x$を右から合成すると、
$y*x^{-1}*x=e_a*x$
$y=x$
である。
したがって、$f(x)=f(y)$ならば$x=y$
が成り立つ。
これより、$Ker(f)=\lbrace e_a \rbrace$ $⇒$ $f$が単射
が示された…②
①②より、
$f$が単射 $⇔$ $Ker(f)=\lbrace e_a \rbrace$
である。
(証明終了)
さて、$Im(f)$が全射の判定に使えたように、
$Ker(f)$は単射の判定に使えることが分かりました。
ところで、$Im(f)$は$B$の部分群です。
$Ker(f)$も何か似たような性質はないのでしょうか?

ひとまず、図より$Ker(f) \subset A$
は分かります。
さて。
$Ker(f)$は$A$の部分群になるのでしょうか?
答えは、部分群どころか、正規部分群になる!です!!!!
(核の性質② 正規部分群)
$f$を群$A$から群$B$への準同型写像とする。
このとき、$f$の核$Ker(f)$は、
$A$の正規部分群となる。
証明に際しては、まず$Ker(f)$が$A$の部分群であることを示して、
次に正規部分群であることを示していく流れになります。
その際、単位元についての準同型写像の性質と、
逆元についての準同型写像の性質を使います。
(単位元についての準同型写像の性質)
$f$を群$A$から群$B$への準同型写像とする。
また、$A$の単位元を$e_a$とし、$B$の単位元を$e_b$とする。
このとき、$f(e_a)=e_b$となる。
(逆元についての準同型写像の性質)
$f$を群$A$から群$B$への準同型写像とする。
このとき、$A$の任意の元$a$について、
$f(a^{-1})=f(a)^{-1}$
が成り立つ。
証明は以下の記事を参照してください

また、正規部分群の定義をおさらいしておきましょう。
(正規部分群の定義)
群$G$と、その部分群$H$がある。
$g \in G$について、
$gHg^{-1}=H$
が成立するとき、$H$を$G$の正規部分群という。
なんで正規部分群なんんてものを考えるか興味がある方はぜひ以下の記事をご覧ください

では、証明をしていこうと思います。
(核が正規部分群である証明)
演算$*$についての群$A$と、演算$〇$についての群$B$を考える。
また、$A$の単位元を$e_a$とし、$B$の単位元を$e_b$とする。
$f$を群$A$から群$B$への準同型写像とする。
このとき、$f$の核 $Ker(f)=\lbrace a \in A \mid f(a)=e_b \rbrace$
が$A$の正規部分群となることを示す。
まずは、$Ker(f)$が$A$の部分群であることを示す。
そのために、まず$Ker(f)$が空集合でないことを確認する。
単位元についての準同型写像の性質より、
$f(e_a)=e_b$
である。したがって、$e_a \in Ker(f)$となり、
$Ker(f)$が空集合でないことが確認できた…①
次に、$Ker(f)$が演算$*$について閉じていることを示す。
$x, y \in Ker(f)$について、$x*y \in Ker(f)$であればよい。
$x, y \in Ker(f)$より、
$f(x)=e_b, f(y)=e_b$
である。
ここで、
$f(x)〇f(y)$を考える。
$f$は準同型写像なので、
$f(x)〇f(y)=f(x*y)$
である。
左辺について、
$f(x)=e_b, f(y)=e_b$より、
$e_b〇e_b=f(x*y)$
となり、
$f(x*y)=e_b$
となる。
よって、$x*y \in Ker(f)$である…②
つぎに、$x \in Ker(f)$を任意にとったとき、
$x^{-1} \in Ker(f)$であることを確認する。
$x \in Ker(f)$より、
$f(x)=e_b$
である。
この両辺に$f(x)^{-1}$を右から合成する。
$f(x)〇f(x)^{-1}=e_b〇f(x)^{-1}$
ここで、逆元についての準同型写像の性質より、
$f(x)^{-1}=f(x^{-1})$であったので、
$f(x)〇f(x)^{-1}=e_b〇f(x^{-1})$
となり、
$f(x^{-1})=e_b$
であるので、$x^{-1} \in Ker(f)$である…③
①②③より、$Ker(f)$ は $A$ の部分群である。
次に、$Ker(f)$が$A$の正規部分群であることを示す。
つまり、$a \in A$をとったとき、
$a(Ker(f))a^{-1}=Ker(f)$
であればよい。
そのためには
$Ker(f) \subset a(Ker(f))a^{-1}$
と
$a(Ker(f))a^{-1} \subset Ker(f)$
を示せばよい。
$Ker(f) \subset a(Ker(f))a^{-1}$
は明らか。
$a(Ker(f))a^{-1} \subset Ker(f)$
を示す。$a \in A$を固定して
$x \in Ker(f)$を任意のに取ったとき、
$a*x*a^{-1} \in Ker(f)$
であればよい。
そのために、$f(a*x*a^{-1})=e_b$を示せばよい。
$f$は準同型写像なので、
$f(a*x*a^{-1})=f(a)〇f(x)〇f(a^{-1})$
である。$x \in Ker(f)$より、$f(x)=e_b$
$f(a*x*a^{-1})=f(a)〇f(x)〇f(a^{-1})$
$=f(a)〇e_b 〇f(a)^{-1}$
$=f(a)〇f(a)^{-1}$
$=f(a)〇f(a^{-1})$
$=f(a*a^{-1})$
$=f(e_a)$
$=e_b$
よって、
$f(a*x*a^{-1})=e_b$
となり、$Ker(f)$が$A$の正規部分群であることが示された
(証明終了)
まとめ
群$A$から群$B$への準同型写像を$f$とします。
・$Im(f)$は$f$が全射であることの判定に使える
・$Ker(f)$は$f$が単射であることの判定に使える
・$Im(f)$は$B$の部分群
・$Ker(f)$は$A$の正規部分群
以上を押さえていただければと思います。

コメント