ガロア理論では、方程式が代数的に解けるための必要十分条件を導くことができます。
そのための道具として必要不可欠なのがガロア拡大と、ガロア群です。
本記事では、この2つの概念について、なぜそんな定義になっているのかといった
発想まで含めて具体的に解説していこうと思います。
ガロア拡大の定義
まず初めにガロア拡大の定義を示しておこうと思います。
その際、体の拡大と拡大次数についての知識や、
$L$の$K$上の自己同型といった知識が必要になりますので、
$L/K$という記号や$[L:K]$という記号、$Aut_K(L)$という記号に馴染みのない方はぜひ以下の記事をご覧ください。
体の拡大について
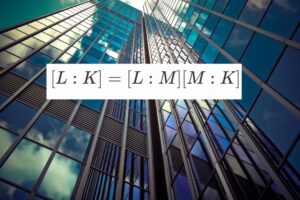
自己同型について

では、ガロア拡大の定義を紹介します。
次のような感じです。
(ガロア拡大の定義)
$L/K$ を有限次の体拡大とする。
このとき、$\mid Aut_K(L) \mid =[L:K]$
であるならば、$L/K$ をガロア拡大という。
続いて、ガロア群の定義を紹介します。
(ガロア群の定義)
有限次の体拡大$L/K$がガロア拡大であるとき、
$Aut_K(L)$を$L/K$のガロア群といい、$Gal(L/K)$で表す。
(要するに、$Gal(L/K)=Aut_K(L)$ ということです)
では、次の見出しでガロア拡大とガロア群の具体例を見ていきましょう。
ガロア拡大とガロア群の具体例
新たに学んだ数学概念の理解を深めるには、具体例を調べてみることが一番です。
ここでは3つの例を見ていこうと思います。
1つ目の例
まずは$\mathbb{Q}(\sqrt{2})/\mathbb{Q}$がガロア拡大であるかどうか調べてみましょう。
定義通り$\mid Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt{2})) \mid =[\mathbb{Q}(\sqrt{2}):\mathbb{Q}]$
が成り立つかどうか調べましょう。
まず、$\mathbb{Q}(\sqrt{2})=\lbrace a+b\sqrt{2} \mid a, b \in \mathbb{Q} \rbrace$
だったので、$\mathbb{Q}(\sqrt{2})/\mathbb{Q}$の拡大次数は2です。
つまり$[\mathbb{Q}(\sqrt{2}):\mathbb{Q}]=2$ です。
では次に$Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt{2})) $を考えていきましょう。
$\sigma \in Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt{2}))$
とします。
$\sqrt{2}$は$x^2-2=0$の解です。
(より正確に言うなら、$\sqrt{2}$の$\mathbb{Q}$上の最小多項式は$x^2-2=0$ )
$\sigma$は四則演算を保存します。
$(\sqrt{2})^2-2=0$の両辺に$\sigma$を作用させましょう。
$\sigma((\sqrt{2})^2-2)=\sigma(0)$
$\lbrace \sigma(\sqrt{2})\rbrace^2-\sigma(2)=\sigma(0)$
ここで、$\sigma$は$\mathbb{Q}$の元を不変に保つので、
$\lbrace \sigma(\sqrt{2})\rbrace^2-2=0$です。
$\lbrace \sigma(\sqrt{2})\rbrace^2=2$となり、
このことから、$\sigma(\sqrt{2})=\pm \sqrt{2}$と分かります。
$\sigma(\sqrt{2})=\sqrt{2}$となる$\sigma$を$e$で表すことにします。
($e$はつまり恒等写像ですね)
$\sigma(\sqrt{2})=-\sqrt{2}$となる$\sigma$はそのまま$\sigma$で表すこととしましょう。
$\sigma$で$\sqrt{2}$を飛ばした先の
$-\sqrt{2}$も$\mathbb{Q}(\sqrt{2})$の元なので、
これは自己同型写像です。
すると、$Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt{2}))=\lbrace e, \sigma \rbrace$
と分かります。
ゆえに、$\mid Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt{2})) \mid =2$
です。
$\mid Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt{2})) \mid =[\mathbb{Q}(\sqrt{2}):\mathbb{Q}]$
が成り立ち、$\mathbb{Q}(\sqrt{2})/\mathbb{Q}$はガロア拡大であると分かります。
2つ目の例
次は$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$がガロア拡大であるかどうか調べてみましょう。
$\mathbb{Q}(\sqrt{2})/\mathbb{Q}$がガロア拡大だったので、
調べるまでもなく$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$もガロア拡大な気はしますが、
それでも実際に確かめてみるという作業は数学では結構大切だったりします。
先ほどと同じ流れで行くと、まずは拡大次数から調べていきます。
$\mathbb{Q}(\sqrt[3]{2})=\lbrace a+b\sqrt[3]{2}+c\sqrt[3]{4} \mid a, b, c \in \mathbb{Q} \rbrace$
です。ゆえに、$[\mathbb{Q}(\sqrt[3]{2}):\mathbb{Q}]=3$となります。
($\mathbb{Q}(\sqrt[3]{2})$がちゃんと四則演算で閉じているかどうかが気になる方はぜひ以下の記事をご覧ください。割り算で閉じていることをチェックする際に有理化を行いますが、その方法が少々テクニカルです。何年度だったか忘れましたが、確か結構最近の京大でこの有理化がモチーフになった問題が出題されました。)

次に$Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt[3]{2}))$を考えていきましょう。
$\sigma \in Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt[3]{2}))$とします。
$\sqrt[3]{2}$は$x^3-2=0$の解です。
($\sqrt[3]{2}$の$\mathbb{Q}$上の最小多項式はx^3-2=0)
ゆえに、$(\sqrt[3]{2})^3-2=0$
です。両辺に$\sigma$を作用させると、
$\sigma \lbrace (\sqrt[3]{2})^3-2 \rbrace=\sigma(0)$
$\lbrace \sigma(\sqrt[3]{2})\rbrace^3-\sigma(2)\sigma(0)$
$\lbrace \sigma(\sqrt[3]{2})\rbrace^3-2=0$
$\lbrace \sigma(\sqrt[3]{2})\rbrace^3=2$
これを解くと、
$\sigma(\sqrt[3]{2})=\sqrt[3]{2}, \omega \sqrt[3]{2}, \omega^2 \sqrt[3]{2}$
となります。ただし、$\omega$は$1$の3乗根のうち、実数でないものです。
($x^3-1=0$から、$(x-1)(x^2+x+1)=0$ となるので、
$\omega$は要するに$x^2+x+1=0$の解です)
$\sigma(\sqrt[3]{2})=\sqrt[3]{2}$の時は$\sigma=e$と表すことにし、
$\sigma(\sqrt[3]{2})=\omega \sqrt[3]{2}$の時は$\sigma=\sigma_1$と表すことにし、
$\sigma(\sqrt[3]{2})=\omega^2\sqrt[3]{2}$の時は$\sigma=\sigma_2$と表すことにすれば、
$Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt[3]{2}))=\lbrace e, \sigma_1, \sigma_2 \rbrace$
となるように思えるのですが、
実はこれは成り立ちません
なぜか?
$\omega \sqrt[3]{2}, \omega^2 \sqrt[3]{2} \notin \mathbb{Q}(\sqrt[3]{2})$だからです。
$\sigma_1$と$\sigma_2$を$\mathbb{Q}(\sqrt[3]{2})$に作用させると、有理数以外の元は
$\mathbb{Q}(\sqrt[3]{2})$の外側の世界に飛んで行ってしまうので、自己同型写像になり得ません。
ゆえに、今回については
$Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt[3]{2}))=\lbrace e \rbrace$
なのです。恒等写像だけ集合です。
したがって、$\mid Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt[3]{2})) \mid=1$
となり、
$\mid Aut_{\mathbb{Q}}(\mathbb{Q}(\sqrt[3]{2})) \mid \neq [\mathbb{Q}(\sqrt[3]{2}):\mathbb{Q}]$
なので、
$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$はガロア拡大ではないと分かります。
3つ目の例
先ほどの観察から、$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$はガロア拡大ではないと分かりました。
では$\sqrt[3]{2}$を含むような拡大はガロア拡大にはなり得ないのでしょうか?
そんなことはありません。
次は$\mathbb{Q}(\omega ,\sqrt[3]{2})/\mathbb{Q}$を考えていきましょう。
まずは拡大次数から。
$\mathbb{Q}(\omega, \sqrt[3]{2})$は、
要するに$\mathbb{Q}$に$\omega$を添加した後に更に$\sqrt[3]{2}$を添加した体です。
これを式にしましょう。
記号がややこしくなるので、$K_0=\mathbb{Q}(\omega)$と表すことにすると、
$\mathbb{Q}(\omega, \sqrt[3]{2})=K_0(\sqrt[3]{2})$です。
$K_0(\sqrt[3]{2})=\lbrace a+b\sqrt[3]{2}+c\sqrt[3]{4} \mid a, b, c \in K_0 \rbrace$
となります。ここで、$a, b, c \in K_0=\mathbb{Q}(\omega)$なので、
$a=x_1+y_1\omega+z_1\omega^2 $ $(x_1, y_1, z_1 \in \mathbb{Q})$
と表すこととしたいのですが、実はもう少し簡略化できます。
$\omega$は要するに$x^2+x+1=0$の解なので、
$\omega^2+\omega+1=0$となり、
$\omega^2=-\omega-1$なのです。
したがって、
$a=x_1+y_1\omega+z_1\omega^2 $
$=x_1+y_1\omega+z_1(-\omega-1)$
$=(x_1-z_1)+(y_1-z_1)\omega$
となるので、結果的に、
$a=X_1+Y_1\omega$ $(X_1, Y_1 \in \mathbb{Q})$と表されます。
同様に、
$b=X_2+Y_2\omega , $
$c=X_3+Y_3\omega$
$(X_2, Y_2, X_3, Y_3 \in \mathbb{Q})$
となります。これを$a+b\sqrt[3]{2}+c\sqrt[3]{4} $
に代入して整理すると、
$a+b\sqrt[3]{2}+c\sqrt[3]{4} $
$=(X_1+Y_1\omega)+(X_2+Y_2\omega)\sqrt[3]{2}+(X_3+Y_3\omega)\sqrt[3]{4}$
$=X_1+Y_1\omega+X_2\sqrt[3]{2}+Y_2\omega\sqrt[3]{2}+X_3\omega\sqrt[3]{4}+Y_3\omega\sqrt[3]{4}$
です。ゆえに、
$[\mathbb{Q}(\omega, \sqrt[3]{2}):\mathbb{Q}]=6$
と分かります。
次は$Aut_{\mathbb{Q}}(\mathbb{Q}(\omega, \sqrt[3]{2}))$を考えていきましょう。
例えば、$\omega \sqrt[3]{2} \in \mathbb{Q}(\omega, \sqrt[3]{2})$なので、
これについて考えます。
$\sigma \in Aut_{\mathbb{Q}}(\mathbb{Q}(\omega, \sqrt[3]{2}))$とします。
$\sigma(\omega \sqrt[3]{2})$を考えましょう。
$\sigma$は四則演算を保存するので、
$\sigma(\omega \sqrt[3]{2})=\sigma(\omega)\sigma(\sqrt[3]{2})$です。
このことから、$\sigma$は$\omega$の飛ばし先と$\sqrt[3]{2}$の飛ばし先の
両方を確定させないと定まらない写像であることが分かります。
まずは$\sigma(\omega)$を考えましょう。
$\omega$は$x^2+x+1=0$の解です。
($\omega$の$\mathbb{Q}$上の最小多項式は$x^2+x+1=0$)
(ちなみに$x^2+x+1=0$の解は$x=\omega, \omega^2$です)
したがって $\omega^2+\omega+1=0$
が成り立ち、この両辺に$\sigma$を作用させると
$\sigma(\omega^2+\omega+1)=\sigma (0)$
$\lbrace \sigma(\omega)\rbrace^2+\sigma(\omega)+1=0$
$x^2+x+1=0$の解は$x=\omega, \omega^2$
なので、$\sigma(\omega)=\omega, \omega^2 \cdots ①$
次に$\sigma(\sqrt[3]{2})$を考えていきますが、
これは先ほどの$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$と同じ議論で、
$\sqrt[3]{2}$が$x^3-2=0$の解であることを利用すると
$\sigma(\sqrt[3]{2})=\sqrt[3]{2}, \omega\sqrt[3]{2}, \omega^2\sqrt[3]{4} \cdots ②$
であることが分かります。
①②から$\sigma$を定めていきましょう。
$\sigma(\omega)=\omega, \sigma(\sqrt[3]{2})=\sqrt[3]{2}$のとき、$\sigma=e$(恒等写像)とし、
$\sigma(\omega)=\omega, \sigma(\sqrt[3]{2})=\omega \sqrt[3]{2}$のとき$\sigma=\sigma_1$
$\sigma(\omega)=\omega, \sigma(\sqrt[3]{2})=\omega^2 \sqrt[3]{2}$のとき$\sigma=\sigma_2$
$\sigma(\omega)=\omega^2, \sigma(\sqrt[3]{2})=\sqrt[3]{2}$のとき$\sigma=\sigma_3$
$\sigma(\omega)=\omega^2, \sigma(\sqrt[3]{2})=\omega \sqrt[3]{2}$のとき$\sigma=\sigma_4$
$\sigma(\omega)=\omega^2, \sigma(\sqrt[3]{2})=\omega^2 \sqrt[3]{2}$のとき$\sigma=\sigma_5$
としましょう。
すると、
$Aut_{\mathbb{Q}}(\mathbb{Q}(\omega, \sqrt[3]{2}))=\lbrace e, \sigma_1, \sigma_2, \sigma_3, \sigma_4, \sigma_5 \rbrace$
となり、
$\mid Aut_{\mathbb{Q}}(\mathbb{Q}(\omega, \sqrt[3]{2})) \mid =6$
であることが分かります。
このことから、
$\mid Aut_{\mathbb{Q}}(\mathbb{Q}(\omega, \sqrt[3]{2})) \mid =[\mathbb{Q}(\omega, \sqrt[3]{2}):\mathbb{Q}]$
となり、
$\mathbb{Q}(\omega, \sqrt[3]{2})/\mathbb{Q}$はガロア拡大であると分かります。
ガロア拡大とガロア群の定義の意味
もう一度ガロア拡大とガロア群の定義を確認しておこうと思います。
(ガロア拡大の定義)
$L/K$ を有限次の体拡大とする。
このとき、$\mid Aut_K(L) \mid =[L:K]$
であるならば、$L/K$ をガロア拡大という.
(ガロア群の定義)
有限次の体拡大$L/K$がガロア拡大であるとき、
$Aut_K(L)$を$L/K$のガロア群といい、$Gal(L/K)$で表す。
(要するに、$Gal(L/K)=Aut_K(L)$ ということです)
はい。
なんでこんなもんを考えようと思ったんだよ!
そう思われたことでしょう。
とりあえずこれはこういうもんなのだ!と受け入れてしまうのもありなのですが、
やっぱり意味を考えたくなるのが人情です。
方程式が解けるための必要十分条件を調べる過程でガロアがガロア理論を構築し、
それをアルティンが線形代数や体や自己同型を使って洗練した形に整えました。
整理すると、
①方程式を解くうえで、「解と係数の関係」と「対称式の基本定理」のコンボが強力だった。
②対称性を記述するために並べ替えを数学的に記述する必要があり、群が生まれた
③方程式を解くということは係数体の世界を、解を含む世界まで広げていくこと
④ゆえに、体の拡大と、並べ替えを結びつける数学的な道具がほしい
⑤それが体の自己同型群であった
ここまでの流れが、前回の記事までで扱ってきた内容の全貌です。
前回の記事

今回はさらに先に進んでいきましょう。
自己同型群$Aut_K(L)$が大切であることは今までの流れから分かるのですが、
なぜ数学者たちは$\mid Aut_K(L) \mid =[L:K]$という条件に着目したのでしょう?
それは、先ほどの具体例の観察結果を見ると、なんとなく見えてきます。
ガロア理論は方程式についての理論です。
(実際は方程式以外にもめちゃくちゃ応用性のある理論ですが、ひとまずここでは方程式についての理論として捉えます。)
$\mathbb{Q}(\omega, \sqrt[3]{2})/\mathbb{Q}$
は定義よりガロア拡大ですが、
$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$
はガロア拡大ではありません。
両者の違いはなんでしょうか?
$\sqrt[3]{2}$に着臆して考えていきましょう。
$\sqrt[3]{2}$はそもそもどんな数だったでしょうか?
$\sqrt[3]{2}$は、$x^3-2=0$の解です。
$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$
の$\mathbb{Q}(\sqrt[3]{2})$は $x^3-2=0$ の解である $\omega \sqrt[3]{2}$ と$ \omega^2 \sqrt[3]{2}$ を
含みません。ゆえに、$x^3-2=0$という方程式を解くうえで、
$\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$という世界の広げ方はうまい広げ方ではないのです。
一方、$\mathbb{Q}(\omega, \sqrt[3]{2})/\mathbb{Q}$
の$\mathbb{Q}(\omega, \sqrt[3]{2})$は、$x^3-2=0$の解を全て含んでいます。
ゆえに、$x^3-2=0$を解くうえで、
$\mathbb{Q}(\omega, \sqrt[3]{2})/\mathbb{Q}$という世界の広げ方は、
うまい広げ方であると言うことができます。
どうでしょうか?
ここまでの考察から、$\mid Aut_K(L) \mid =[L:K]$という条件は、
世界の広げ方がうまい広げ方であるか否であるかをジャッジする条件なのではないか?
という予想が立ちます(この予想は正しいことが証明できますので今後の記事にご期待下さい)。
だから数学者たちは、$\mid Aut_K(L) \mid =[L:K]$という条件をガロア拡大の定義に採用したのです!
(ガロア理論黎明期の数学者たちに直接会ったわけではないですが、多分そうだと思います。)
まとめ
いかがでしたか?
・方程式を解くということは、係数体の世界を解を含む世界まで広げること
・ただやみくもに体の世界を広げていっても、解を含む世界までたどり着くことはできない
・$\mid Aut_K(L) \mid =[L:K]$という条件を満たすように世界を広げると、
解を含む世界まで上手にたどり着けるっぽい(いまはまだ予想。しかもちょっと修正が必要)
・だから$\mid Aut_K(L) \mid =[L:K]$を満たす体の拡大に特別な名前を付けよう!
・ガロア拡大爆誕!
以上の流れが僕の解釈です。
多分こんな感じでガロアのアイデアは現代数学風にアレンジされていったのではないでしょうか。
実際どうだったかは最早知る由もありませんが、考えてみるのは楽しいものです。
ちなみに、ガロア拡大には他にも同値な表現が何通りかあり、
アルティン流、雪江流、石井流などの流派があります。
(勝手に僕が分類しただけです。どの先生のことも尊敬しています)
いずれはガロア拡大の同値表現を一覧でまとめた記事を作りたいなと思っています。
ではまた次回の記事でお会いしましょう!
参考
[1] エミール・アルティン, ガロア理論入門, 筑摩書房, 2010
[2] 中島匠一, 代数方程式とガロア理論, 共立出版, 2006
画像素材提供(アイキャッチ):Tobias BrunnerによるPixabayからの画像
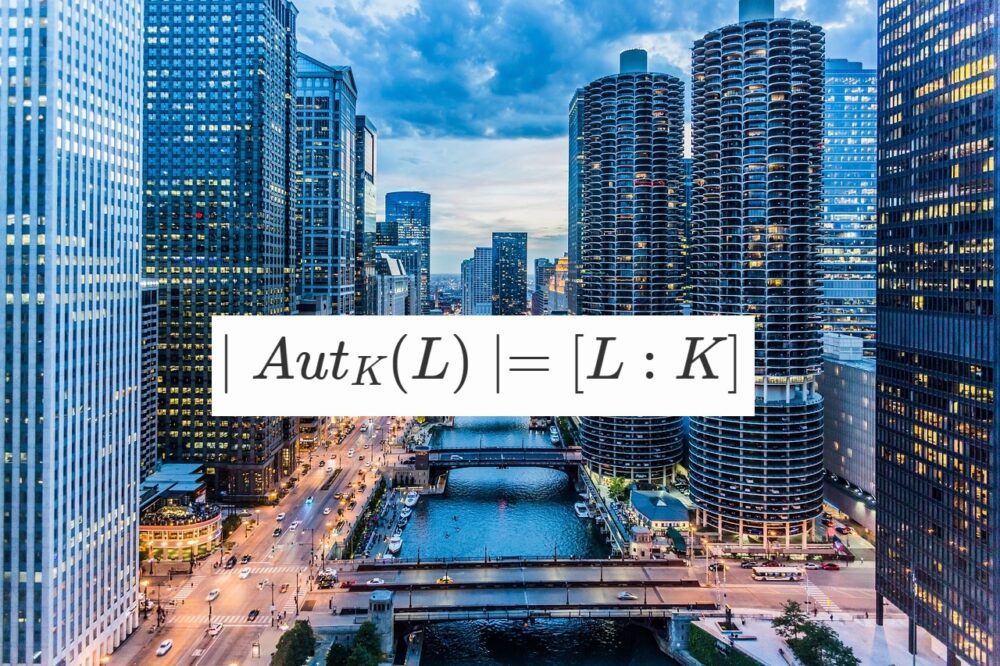
コメント
コメント一覧 (2件)
73歳、数学を楽しんでいます、ガロアさんには、10年前お会いしましたが、剰余類、正規部分群、辺りで、ひっくり返って二度と立ち上がれないだろうと思っていましたが、貴サイトのガロアさん関係の記事に接して、再起動しました。今度こそ、ガロアさんとお目にかかれるかな・・・・?
田中康文さん
コメントありがとうございます!
当ブログの記事が少しでもお役に立てたなら幸甚です!
群の定義がなぜあのような形になっているか、
正規部分群でなぜgH=Hgという条件を考える必要があるか等も
他の記事で扱っていますので、ぜひご覧くださいませ。
田中さんとガロアさんの出会いを応援しております!