今回は体の拡大次数について具体例で学んでいきます。
簡単に言うと、拡大次数は体の世界がどのくらい広がっているのかを数値化したものです。
方程式論においてとても重要な役割を演じます。
頑張っていきましょう!
体(たい)とは?
体とは、簡単に言えば四則演算で閉じた集合のことです。
例えば、自然数$\mathbb{N}$を考えましょう。
$\mathbb{N}=\lbrace 1, 2, 3, \cdots \rbrace$
です。
$3, 4 \in \mathbb{N}$に対して、
$3+4=7 \in \mathbb{N}$です。
このように、自然数$N$は足し算について閉じています。
では、引き算はどうでしょうか?
$3, 4 \in \mathbb{N}$に対して、
$3-4=-1 \notin \mathbb{N}$です。
したがって、自然数$N$は引き算について閉じていないので、体ではありません。
このように、体は結構レアな存在なのです。
自然数、整数、有理数、実数、複素数と数の概念は広がっていきますが、
この中では有理数$\mathbb{Q}$が最初に登場するの体です。
では、なぜ体という概念が必要なのでしょう?
それは、一次方程式と解くときに四則演算を使うからです。
どういうことでしょうか?
一次方程式は、$ax+b=0$で表されます。
より丁寧にみると、$a×x+b=0$なので、この時点で足し算と掛け算は必要です。
そして、$b$を移項して$ax=-b$を得る際に引き算を使います。
最後に、両辺を$a$で割って$x=\dfrac{b}{a}$を得る際に割り算を使います。
このように、方程式を解く際には、係数となる数の集合に四則演算で閉じていることが要求されるのです。
そして、「体」と「並び変え」の本質的な違いを深堀っていくと、
「群」の定義がとても自然に感じられるようになります。
今回の記事では深堀しないですが、興味のある方はぜひ以下の記事をご覧ください。

次の見出しでは、体の拡大について考えていきましょう。
体の拡大について
この見出しでは、言葉の定義を紹介していきます。
(拡大体の定義)
体$K$があり、$L$は$K$を含む体であるとする。
(つまり$K \subset L$です)
このとき、$L$は$K$の拡大体であるという。
(記号$L/K$の定義)
$L$が体$K$の拡大体であるとき、
これを$L/K$は体の拡大である、と表現する
(中間体の定義)
体の拡大$L/K$について、$K \subset M \subset L$となる$M$が存在するとき、
$M$を$L/K$の中間体という。
ではここで小休憩。
「$/$」という記号は要注意です。
この記号は、群に使われているのか体に使われているのかで大きく意味が変わります。
体に使われている場合は、上で確認した通り、体の拡大を表しています
しかし、群に対して使われたときは、剰余群を表します。
例えば、$\mathbb{Z}/3\mathbb{Z}$は剰余群です。
このように、「$/$」という記号は体の文脈で使われているのか群の文脈で使われているのか見極めないと
混乱するので(経験者は語る)、気を付けましょう。
さて。
体の拡大って何が便利なの?
と疑問に思っておられることでしょう。
その答えは、
拡大体を線形空間とみなすことができるという点に尽きます。
それを次の見出しで確認していきましょう
拡大次数について
ここの見出しでは、「既約と可約」と「線形空間」と「次元」を基礎知識として扱います。
これらの言葉に馴染みのない方は、以下の記事をご覧ください。
↓既約と可約について

↓線形空間について

↓次元について

ではここから本題に入っていきましょう。
方程式の話に立ち返って、体の拡大の便利さを考えていきたいと思います。
例えば、$x^2-3=0$を解くとき、どうやっていましたっけ?
まず、$x^2-3=0$の係数の範囲は有理数です。
そして、$x-2-3=0$は有理数係数の範囲で既約(これ以上因数分解できない)です。
なので、これを因数分解しようと思ったら、係数の世界を
有理数$\mathbb{Q}$から$\mathbb{Q}(\sqrt{3})$まで広げる必要があります。
$\mathbb{Q}$の範囲では$x^2-3=0$は既約ですが、
$\mathbb{Q}(\sqrt{3})$の範囲では可約になって、
$x^2-3=(x-\sqrt{3})(x+\sqrt{3})$
と因数分解できます。
このように、方程式を解くとは、
1次式に分解できるまで係数の世界を広げること
と解釈することができます。
係数世界を広げる?
じゃあどんくらい広げるんだよ!?
というのが次の問題です。
「広げる」という表現は非常にあいまいな言葉なので、数学的ではありません。
係数の世界をどのくらい広げているのか、という点をしっかり定義して数値で表していきたいわけです。
$\mathbb{Q}(\sqrt{3})=\lbrace a+b\sqrt{3} \mid a, b \in \mathbb{Q} \rbrace$
でした。
$\mathbb{Q} \subset \mathbb{Q}(\sqrt{3})$
であり、$\mathbb{Q}$も$\mathbb{Q}(\sqrt{3})$も体なので、
$\mathbb{Q}(\sqrt{3})/\mathbb{Q}$は体の拡大となります。
ここで、線形空間の知識を使います。
$\mathbb{Q}(\sqrt{3})$は、$\mathbb{Q}$上の線形空間です。
そして、基底は$\lbrace 1, \sqrt{3} \rbrace$なので、次元は2です。
すなわち、$\dim_\mathbb{Q}(\mathbb{Q}(\sqrt{3}))=2$
です。
これです!
この数値が、係数のがそのくらい広がったかを表していると捉えるととても都合がよいのです。
(拡大次数の定義)
$L/K$を体の拡大とし、$L$は$K$上の線形空間であるとする。
このとき、$\dim_K(L)$を$L/K$の拡大次数と言い、
$\dim_K(L)=[L:K]$で表す。
では続いて具体例を見ていきましょう。
拡大次数の具体例
有理数に3の平方根を添加した場合
まずは$\mathbb{Q}$と$\mathbb{Q}(\sqrt{3})$について考えましょう。
$\mathbb{Q}(\sqrt{3})$は$\mathbb{Q}$上の線形空間であり、
基底は$\lbrace 1. \sqrt{3} \rbrace$
で$\dim_\mathbb{Q}(\mathbb{Q}(\sqrt{3}))=2$
となるため、
$[\mathbb{Q}(\sqrt{3}):\mathbb{Q}]=2$です。
有理数に2の三乗根を添加した場合
次に$\mathbb{Q}$と$\mathbb{Q}(\sqrt[3]{2})$を考えていきましょう。
そもそも、$\mathbb{Q}(\sqrt[3]{2})$ってなんでしょう?
そては、$\mathbb{Q}$と$\sqrt[3]{2}$の四則演算であられる数全体の集合です。
$\mathbb{Q}(\sqrt{2})$の時と同じノリで考えたら、
$\mathbb{Q}(\sqrt[3]{2})=\lbrace a+b\sqrt[3]{2} \mid a, b \in \mathbb{Q} \rbrace$
となりそうな気がしますが、残念ながら、これは正しくありません。
なぜか?
$\sqrt[3]{2} \in \mathbb{Q}(\sqrt[3]{2})$ですので、
当然$\sqrt[3]{2}×\sqrt[3]{2} \in \mathbb{Q}(\sqrt[3]{2})$でなければなりません。
(体であるには、掛け算について閉じていてほしい)
しかし、
$\sqrt[3]{4} \notin \lbrace a+b\sqrt[3]{2} \mid a, b \in \mathbb{Q} \rbrace$
です。
ゆえに、
$\mathbb{Q}(\sqrt[3]{2})=\lbrace a+b\sqrt[3]{2}+c\sqrt[3]{4} \mid a, b, c\in \mathbb{Q} \rbrace$
これ、本当に体になっているでしょうか?
足し算、引き算、掛け算について閉じていることは比較的すぐに分かります。
でも、割り算について閉じているかは一苦労です。
すなわち、
$\dfrac{x+y\sqrt[2]{3}+z\sqrt[3]{4}}{a+b\sqrt[2]{3}+c\sqrt[3]{4}} \in \mathbb{Q}(\sqrt[3]{2})$
であるかどうかを調べなければなりません。
結論から述べると、これは体です。
うまく有理化することができます。
ちなみに、有理化には$a^3+b^3+c^3-3abc$の因数分解を用います。
詳しくは、、以下の記事をご覧ください

ここまでの議論から、
$\mathbb{Q}(\sqrt[3]{2})=\lbrace a+b\sqrt[3]{2}+c\sqrt[3]{4} \mid a, b, c\in \mathbb{Q} \rbrace$
の基底が$\lbrace 1, \sqrt[3]{2}, \sqrt[3]{4} \rbrace$
であることが分かります。
$\mathbb{Q}(\sqrt[3]{2})$は$\mathbb{Q}$上の線形空間なので、
$[\mathbb{Q}(\sqrt[3]{2}):\mathbb{Q}]=3$
となります。
有理数に2の平方根と3の平方根を添加した場合
では、次は$\mathbb{Q}(\sqrt{2})$に$\sqrt{3}$を添加してみましょう。
ちょっと記号がややこしくなるので、
$\mathbb{Q}(\sqrt{2})=K$と置きましょう。
今考えるべき体は、$K(\sqrt{3})$です。
$K(\sqrt{3})=\lbrace a+b\sqrt{3} \mid a, b \in K \rbrace$
を考えていくことになります。
ちなみに、この表記は$K(\sqrt{3})$を$K$上の線形空間とみなしています。
$K$上の線形空間としての$K(\sqrt{3})$は、基底が2個なので、拡大次数は2です。
$[K(\sqrt{3}):K]=2$
ではここで少し見方を変えて、$K(\sqrt{3})$を$\mathbb{Q}$上の線形空間をみなしてみましょう。
$K(\sqrt{3})=\lbrace a+b\sqrt{3} \mid a, b \in K \rbrace$
について、$a \in K$で$K=\mathbb{Q}(\sqrt{2})$なので、
$a=a_1+a_2\sqrt{2}(a_1. a_2 \in \mathbb{Q})$です。
同様に、
$b=b_1+ab_2\sqrt{2}(b_1. b_2 \in \mathbb{Q})$です。
したがって、
$a+b\sqrt{3}=(a_1+a_2\sqrt{2})+(b_1+b_2\sqrt{2})\sqrt{3}$
$=(a_1+b_1)+a_2\sqrt{2}+b_1\sqrt{3}+b_2\sqrt{6}$
となります。
つまり、
$K(\sqrt{3})=\lbrace x+y\sqrt{2}+z\sqrt{3}+w\sqrt{6} \mid x, y, z, w \in \in \mathbb{Q} \rbrace$
です。
したがって、
$[K(\sqrt{3}):\mathbb{Q}]=4$
となります。
そして、$4=2×2$です。
一度ここまでのことをまとめておきましょう。
・$K=\mathbb{Q}(\sqrt{2})$
・$[K:\mathbb{Q}]=2$
・$[K(\sqrt{3}):K]=2$
・$[K(\sqrt{3}):\mathbb{Q}]=4$
どうですか?
$4=2×2$に上記の結果を代入すると、
$[K(\sqrt{3}):\mathbb{Q}]=[K(\sqrt{3}):K][K:\mathbb{Q}]$
が成り立ちます。
実は、これは一般化することが可能です。
次の見出しでこれを定理化していきましょう。
体の拡大次数に関する定理
(体の拡大位数に関する定理)
$K, M, L$を体とし、$K \subset M \subset L$とする。
このとき、$[L:K]=[L:M][M:K]$が成り立つ
(証明)
$l=[L:M]$とし、$m=[M:K]$とする。
$\lbrace x_1, x_2, \cdots, x_l \rbrace$を$L$の$M$上の基底とし、
$\lbrace y_1, y_2, \cdots, y_m \rbrace$を$M$の$K$上の基底とする。
このとき、
$\lbrace x_1y_1, x_1y_2, x_1y_3, \cdots, x_1y_m, $
$x_2y_1, x_2y_2, \cdots, x_2y_m, $
$x_3y_1, x_3y_2, \cdots, x_3y_m, $
$\cdots, $
$x_ly_1, x_ly_2, \cdots, x_ly_m \rbrace$
について考える。表記を簡略化するため、
これを$A=\lbrace x_iy_j \mid 1≦i≦l, 1≦j≦m \rbrace$
とおく。
$[L:K]=lm$を示すには、
$A$が$L$の$K$上の基底であることを示せばよい。
そのために、$l \in L$に対して、
$l=a_1x_1y_1+a_2x_1y_2+\cdots a_{ml}x_ly_m$
となる$a1, \cdots, a_{ml} \in K$が存在することと、
$A$の各元が線形独立であることを示せばよい。
いま、$\lbrace x_1, x_2, \cdots, x_l \rbrace$が$L$の$M$上の基底であるので、
$l=b_1x_1+b_1x_2+\cdots b_lx_l$ $(b_1, \cdots, b_l \in M)$である。
ここで、各$b_p$ $(p=1. 2. \cdots, l)$に対して、
$b_p=c_1y_1+c_2y_2+\cdots, c_my_m$
となる$c1, c_2, \cdots, c_m \in K$が存在する。
$b_p=c_1y_1+c_2y_2+\cdots, c_my_m$
を$l=b_1x_1+b_1x_2+\cdots b_lx_l$ $(b_1, \cdots, b_l \in M)$
に代入すると、
$l=a_1x_1y_1+a_2x_1y_2+\cdots a_{ml}x_ly_m$となる
$a1, \cdots, a_{ml} \in K$が存在することが分かる。…①
次に、
$A=\lbrace x_iy_j \mid 1≦i≦l, 1≦j≦m \rbrace$
が線形独立であることを示す。
$l=a_1x_1y_1+a_2x_1y_2+\cdots a_{ml}x_ly_m$について、
$a_1x_1y_1+a_2x_1y_2+\cdots a_{ml}x_ly_m=0$のときに
$a_1=a_2=\cdots =a_{ml}=0$であればよい。
いま、
$l=b_1x_1+b_1x_2+\cdots b_lx_l$
となる$b_1, b_2, \cdots, b_l \in M$が存在する。
$\lbrace x_1, x_2, \cdots, x_l \rbrace$を$L$の$M$上の基底であるので、
$l=0$であれば$b=1=b_2= \cdots =b_l=0$である。
ここで、各$b_p$ $(p=1, 2, \cdots, l)$に対して、
$b_p=c_1y_1+c_2y_2+\cdots, c_my_m$となる$c_1, c_2, \cdots, c_m \in K$
が存在する。
$\lbrace y_1, y_2, \cdots, y_m \rbrace$を$M$の$K$上の基底なので、
$b_p=0$であれば$c_1=c_2=\cdots c_m=0$である。
ゆえに、$a_1x_1y_1+a_2x_1y_2+\cdots a_{ml}x_ly_m=0$のとき、
$a_1=a_2=\cdots =a_{ml}=0$である…②
①②より、$A=\lbrace x_iy_j \mid 1≦i≦l, 1≦j≦m \rbrace$は
$L$の$K$上の基底である。
したがって、$[L:K]=ml$となり、
$[L:K]=[L:M][M:K]$が成り立つ
(証明終了)
まとめ
いかがでしたか?
・方程式を解くときは、係数の世界を広げている
・どのくらい世界が広がったかを数値で記述するために、体の拡大次数という概念が便利
以上を押さえていただければと思います。
ではまた次回の記事でお会いしましょう!
参考
画像素材提供(アイキャッチ)Hands off my tags! Michael GaidaによるPixabayからの画像
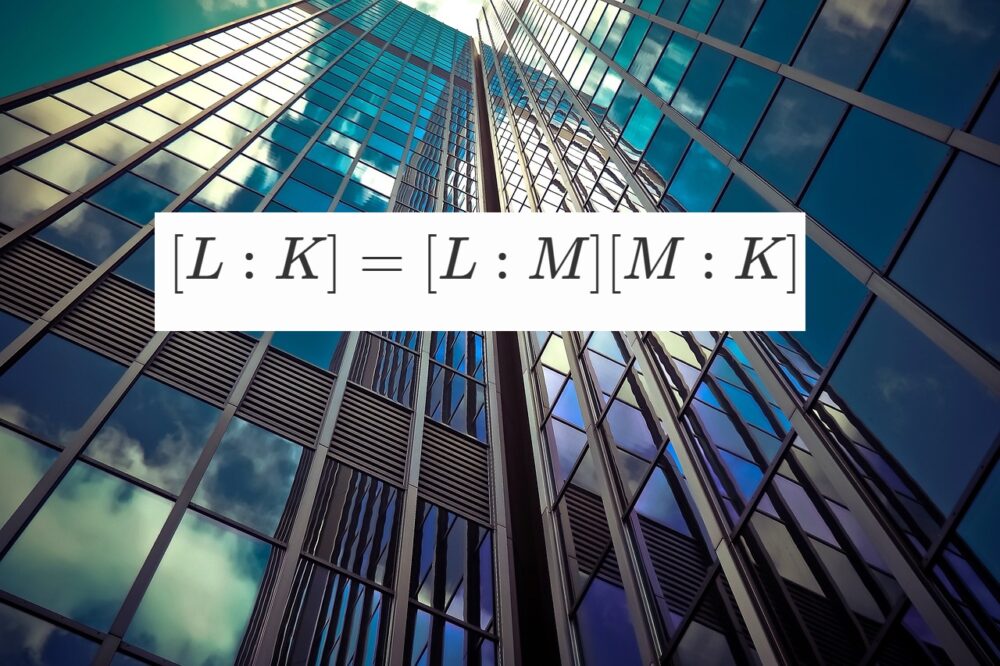
コメント