今回は固定体とガロア拡大の関係について解説していきます。
固定体の定義
まずは固定体の定義を確認しましょう
(固定体の定義)
$L$を体とする。$G$を$Aut(L)$の部分群とする。
このとき、$G$の元によって不変に保たれる$L$の元全体の集合を
$G$の固定体といい、$L^G$で表す。
すなわち、
$L^G=\lbrace x \in L \mid 全ての\sigma \in Gについて \sigma(x)=x \rbrace$
である。
固定体はガロア理論を語るうえで必要不可欠な超重要概念です。
なぜか。
それは、次の見出しで紹介するとってもすっごい定理が成り立つからです
固定体とガロア拡大についての定理
(固定体とガロア拡大についての定理)
$L/K$を有限次の体拡大とする。また、$G$を$Aut_K(L)$の部分群とする。
このとき、$L/K$がガロア拡大となるための必要十分条件は、
$L^G=K$となることである。
ガロア拡大の同値表現第一弾です!
いままでは、ガロア拡大と言えば$\mid Aut_K(L) \mid =[L:K]$でしたが、
他にも色々とガロア拡大の同値表現は存在します。
今回は固定体を使ったものを学んでいきましょう。
必要十分の証明なので、十分性と必要性を分けて証明していきます。
では次の見出しに進んでいきましょう!
固定体⇒ガロア拡大の証明の思考回路と補題
今回の記事でまず最初に証明したいのは以下の定理です。
(固定体⇒ガロア拡大)
$L/K$を有限次の体拡大とする。また、$G$を$Aut_K(L)$の部分群とする。
このとき、$L^G=K$であるならば、$L/K$はガロア拡大となる
ひとまずここの見出しでは、証明のアイデアを確認し、この次の見出しで証明を行います。
証明だけ見たい方は飛ばしてください。
まず一度ガロア拡大の定義を思い出しておきましょう。
(ガロア拡大の定義)
$L/K$ を有限次の体拡大とする。
このとき、$\mid Aut_K(L) \mid =[L:K]$
であるならば、$L/K$ をガロア拡大という。
より詳しくはこちらの記事をご覧ください

この見出しの目的は、$L/K$がガロア拡大を示すことです。
そしてガロア拡大の定義は
$\mid Aut_K(L) \mid =[L:K]$
です。
要するに、$L^G=K$という条件を使って
$\mid Aut_K(L) \mid =[L:K]$
を示すことができればよい、という流れになります。
証明の思考回路
ではここからは証明の発想を整理していこうと思います。
今回の証明はかなり突飛というか、
初見だとなんでそんな変形するんだよ!という突っ込みどころ満載で、
行間を読み取るのが難しいと思うので丁寧に進めていきたいと思います。
まずは目標の確認。
$\mid Aut_K(L) \mid =[L:K]$をゲットすることがゴールです。
ここで、$\mid Aut_K(L) \mid $と$[L:K]$に関して、
アルティン流ガロア理論で重要な定理より、
$\mid Aut_K(L) \mid ≦[L:K]$は直ちに成立します。
とりあえず結果だけ使いましたが、証明が気になる方は以下の記事をご覧ください

あとは$[L:K]≦\mid Aut_K(L) \mid$さえ示すことができれば、
$[L:K]≦\mid Aut_K(L) \mid ≦[L:K]$
となり、
$\mid Aut_K(L) \mid =[L:K]$
を示すことができます。
問題は、どうやって$[L:K]≦\mid Aut_K(L) \mid$を示すかです。
簡略のため、$\mid Aut_K(L) \mid =n$と置きましょう。
$[L:K]≦n$を示せばよいことになります。
これをどうとらえるか。
$[L:K]$は体の拡大次数です。
拡大次数はどうやって定まっていたか?
それは基底の本数で定まりました。
基底の本数はどうやって定まっていたか?
線形独立な元の個数で定まっていました。
$[L:K]≦n$は要するに、
線形独立なものの個数は$n$個以下だよ、と述べているのです。
ということはつまり、$n+1$個の元を集めたらそれは線形独立にならないということです。
線形独立でないということは、線形従属ということ。
要するに、$n+1$個の元を集めたら線形従属になるよ!ということを示すことになります。
もう少し言い換えると、
$u_1, u_2, \cdots, u_{n+1} \in L$をとり、
$a_1, a_2, \cdots, a_{n+1} \in K$に対して
$a_1u_1+a_2u_2+\cdots +a_{n+1}u_{n+1}=0$
としたとき、$a_1, \cdots, a_{n+1}$に$0$でないものが存在することを示せばよいのです。
ではどうやって示すのか?
似たようなシチュエーションを思い返しましょう。
線形従属や線形独立と、体の自己同型写像が絡むような定理の証明はいままでなかったでしょうか?
ありましたよね!「デデキントの補題」や「アルティン流ガロア理論で重要な定理」です!!
あのときの戦略を流用しましょう。
ゴールは
$a_1u_1+a_2u_2+\cdots +a_{n+1}u_{n+1}=0$
が成り立つときに$a_1, \cdots, a_{n+1}$に$0$でないものが存在することを示すことです。
本当にそのような条件を満たす$a_1, \cdots, a_{n+1}$が存在するかは確かめるまで分かりませんが、
$a_1u_1+a_2u_2+\cdots +a_{n+1}u_{n+1}=0$に
$\sigma \in Aut_K(L)$を作用させると、$a_i \in K$ $(i=1, 2, \cdots, n+1)$なので
$Aut_K(L)$の定義から$\sigma(a_i)=a_i$となり
$a_1\sigma(u_1)+a_2\sigma(a_2)+\cdots +\sigma_{n+1}(u_{n+1})=0$…㋐
が成り立つことになります。
$\mid Aut_K(L) \mid =n$と置いているので、
$\sigma_1, \sigma_2, \cdots, \sigma_n$で㋐の式と同じ作業ができます。
すると、連立方程式が出来上がります。
連立方程式っぽさを出すために、$a_i$は$x_i$に変えて、
$x_i$に非自明な解が合ったらそれを$a_i$とするといった流れで行きます。
実際に連立方程式を立式しましょう。
$\begin{equation} \left\{ \, \begin{aligned} & x_1\sigma_1(u_1)+x_2\sigma_1(u_2)+\cdots +x_n\sigma_1(u_n)+x_{n+1}\sigma_{1}(u_{n+1})=0 \cdots ㋑\\ & x_1\sigma_2(u_2)+x_2\sigma_2(u_2)+\cdots +x_n\sigma_2(u_n)+x_{n+1}\sigma_{2}(u_{n+1})=0\cdots ㋒ \\ & \ldots \\ & x_1\sigma_n(u_1)+x_2\sigma_n(u_2)+\cdots +x_n\sigma_2(u_n)+x_{n+1}\sigma_{n}(u_{n+1})=0\cdots ㋓ \end{aligned} \right. \end{equation}$
はい。これは式の数より文字の数の方が多いので必ず非自明な解を持ちます。
この連立方程式の解を$x_1=a_1, x_2=a_2, \cdots, x_{n+1}=a_{n+1}$
と置けば、$a_i$に必ず$0$でないものが一つは存在するので線形従属を示せたことになります。
とはならないところが今回の難しいポイント!!
ちょっと不十分なところがあるんですね。
で、この不十分さをクリアにするための式変形があるのですが、
それが何で必要なのか初見だとマジで意味不明なので、ここにこだわって解説していきたいと思います。
どこが不十分なのか?
改めてゴールを確認しましょう。
要するに、$K$の元$a_i$と$L$の元を取ってきて、
$a_1u_1+a_2u_2+\cdots +a_{n+1}u_{n+1}=0$
が成り立つときに$a_i$に$0$でないものが存在するよ!と言えればよいです。
そのための手段として連立方程式
$\begin{equation} \left\{ \, \begin{aligned} & x_1\sigma_1(u_1)+x_2\sigma_1(u_2)+\cdots +x_n\sigma_1(u_n)+x_{n+1}\sigma_{1}(u_{n+1})=0 \cdots ㋑\\ & x_1\sigma_2(u_2)+x_2\sigma_2(u_2)+\cdots +x_n\sigma_2(u_n)+x_{n+1}\sigma_{2}(u_{n+1})=0\cdots ㋒\\ & \ldots \\ & x_1\sigma_n(u_1)+x_2\sigma_n(u_2)+\cdots +x_n\sigma_2(u_n)+x_{n+1}\sigma_{n}(u_{n+1})=0\cdots ㋓ \end{aligned} \right. \end{equation}$
を解きました。
連立方程式を解くときは、加減法で四則演算を使いますよね。
加減法で文字を減らしていくと、最終的に未知数が連立方程式の係数で表されます。
ここ!!
ここがポイントです。
例えば
$x_1\sigma_1(u_1)+x_2\sigma_1(u_2)+\cdots +x_n\sigma_1(u_n)+x_{n+1}\sigma_{1}(u_{n+1})=0 \cdots $㋑
の式を見てください。
未知数は$x_i$で、係数は$\sigma_1(u_i)$です。
$\sigma_1(u_i) \in L$ですよね。
はい。
連立方程式を解けば非自明な解が見つかってそれを$x_i=a_i$とすれば、
確かに$a_1, a_2, \cdots, a_{n+1}$のどれかが$0$でないこは示せます
でも$a_i$が$K$の元かどうかは分からないのです!!
だって$a_i$は係数の$\sigma_j(u_i)$たちの四則演算で作られていて、$\sigma_j(u_i) \in L$ですから。
このままだと$a_i \in L$なんです。
だからちょっと改良がいるんですね。
どうするか?
この問題を解決するには、
$u_i \in L$たちを材料として作られるけど、必ず$K$の元になるようなものがあればよいです。
そしてそれが$0$にならないことが示されれば線形独立を示すのにめっちゃ役立ちます。
そのために以下の補題を示すことになります。
その際、今までずっと放置されてた$L^G=K$という条件を使います。
補題
(補題)
$L/K$を有限次の体の拡大とし、$G$を$Aut(L)$の部分群とし、
$G=\lbrace \sigma_1, \sigma_2, \cdots, \sigma_{n} \rbrace$と置く。
このとき、$L^G=K$であるならば、
$L$の任意の元$a$に対して
$\sigma_1(a)+\sigma_2(a)+\cdot +\sigma_n(a) \in K$
が成り立つ…㋔
また、$\sigma_1(b)+\sigma_2(b)+\cdots +\sigma_n(b) \neq 0$
となる$b \in L$が存在する。…㋕
証明は比較的簡単です。
$\sigma_1(a)+\sigma_2(a)+\cdot +\sigma_n(a) \in K$
を示せばよく、条件より$K=L^G$なので、
$\sigma_1(a)+\sigma_2(a)+\cdot +\sigma_n(a) \in L^G$
を示せばよいです。
まず㋔を示し、次に㋕を示します。
㋕を示す際にデデキントの補題を使います。
(デデキントの補題)
$K, L$を体とし、$K$から$L$への互いに異なる$n$個の準同型写像を
$\sigma_1, \sigma_2, \cdots, \sigma_n$とする。
このとき、任意の$x \in K$に対して、
$a_1\sigma_1(x)+a_2\sigma_2(x)+\cdots+a_n\sigma_n(x)=0$
($a_1, a_2, \cdots, a_n \in L$)
が成り立つのは
$a_1=a_2=\cdots =a_n=0$のときのみである。
デデキントの補題の証明が気になる方は以下の記事をご覧ください

では補題の証明に進んでいきましょう!
(補題の証明)
$A=\sigma_1(a)+\sigma_2(a)+\cdot +\sigma_n(a)$と置く。
まず$A \in K$を示す。
今、条件より$K=L^G$であるので、
$A \in L^G$を示せばよい。
$L^G$の定義より、
$\sigma \in G$を任意にとったとき、$\sigma(A)=A$であれば$A\in L^G$となるので、
これを示す。
$\sigma(A)=\sigma 〇\sigma_1(a)+\cdots +\sigma 〇\sigma_n(a)$
である。ここで、$\sigma 〇\sigma_i$ $(i=1, 2, \cdots, n)$について考える。
$G$は$Aut(L)$の有限部分群であり、
$G=\lbrace \sigma_1, \sigma_2, \cdots, \sigma_{n} \rbrace$である。
$G$は群なので、$\sigma 〇 \sigma_i \in G$である $(i=1, 2, \cdots, n)$
ここで、$\sigma 〇\sigma_i=\sigma 〇\sigma_j$ $(\sigma_i \neq \sigma_j)$
が成り立つとする.
すると、
$\sigma^{-1}〇\sigma 〇\sigma_i=\sigma^{-1}〇\sigma 〇\sigma_j$
となり、
$\sigma_i =\sigma_j$となって矛盾が発生する。
ゆえに
$\lbrace \sigma_1, \sigma_2, \cdots, \sigma_n \rbrace $
と
$\lbrace \sigma〇\sigma_1, \sigma 〇 \sigma_2, \cdots, \sigma 〇\sigma_n \rbrace$
は元の順番が異なるだけで集合としては等しい…㋖
ここで、$\sigma(A)$を考える。
$\sigma(A)$
$=\sigma \lbrace \sigma_1(a)+\sigma_2(a)+\cdots \sigma_{n}(a) \rbrace$
$=\sigma 〇\sigma_1(a)+\sigma 〇\sigma_2(a)+\cdots +\sigma 〇\sigma_n(a)$
ここで㋖より、
$\lbrace \sigma_1, \sigma_2, \cdots, \sigma_n \rbrace = \lbrace \sigma〇\sigma_1, \sigma 〇 \sigma_2, \cdots, \sigma 〇\sigma_n \rbrace$
であるので、
$\sigma 〇\sigma_1(a)+\sigma 〇\sigma_2(a)+\cdots +\sigma 〇\sigma_n(a)$
$=\sigma_1(a)+\sigma_2(a)+\cdot +\sigma_n(a)$
$=A$
よって$\sigma(A)=A$となり、
$A \in L^G$
である。条件より$L^G=K$なので、
$A \in K$が示された。(←㋔の証明はここで終了。次は㋕についてです。)
ここで、
$\sigma_1(b)+\sigma_2(b)+\cdots +\sigma_n(b) \neq 0$
となる$b \in L$が存在することを背理法で示す。
いま、任意の$b \in L$に対して
$\sigma_1(b)+\sigma_2(b)+\cdots +\sigma_n(b) =0$
であると仮定する。
デデキントの補題より、
$a_1\sigma_1(b)+a_2\sigma_2(b)+\cdots+a_n\sigma_n(b)=0$
が成立するのは$a_1=a_2= \cdots =a_n=0$の時のみでなければいけない。
$1 \neq 0$であるので、これは
$1×\sigma_1(b)+1×\sigma_2(b)+\cdots +1×\sigma_n(b) =0$
に矛盾する。
ゆえに背理法より、
$\sigma_1(b)+\sigma_2(b)+\cdots +\sigma_n(b) \neq 0$
となる$b \in L$が存在する。(←㋕も証明できました!)
(証明終了)
ここまでで証明の発想と補題を確認できたので、
次の見出しで証明を清書していきましょう!
固定体⇒ガロア拡大の証明
(固定体⇒ガロア拡大)
$L/K$を有限次の体拡大とする。また、$G=Aut_K(L)$とする。
このとき、$L^G=K$であるならば、$L/K$はガロア拡大となる
では証明していきましょう!
(固定体⇒ガロア拡大の証明)
$\mid Aut_K(L)\mid=[L:K]$
を示せばよい。
アルティン流ガロア理論で重要な定理より、
$\mid Aut_K(L)≦[L:K]$
が成立する。
あとは$[L:K]≦\mid Aut_K(L)$
を示すことができれば、
$[L:K]≦\mid Aut_K(L)\mid ≦[L:K]$
が成り立ち$\mid Aut_K(L)\mid=[L:K]$
となる。
ゆえに$[L:K]≦\mid Aut_K(L)$を示す。
$\mid Aut_K(L)\mid =n$
と置くと、
$[L:K]≦n$
を示せばよいことになる。
つまり、$L$の$n+1$個の元が必ず$K$上線形従属であることを示せばよい
いま、$u_1, u2, \cdots, u_{n+1} \in L$を取り、
$x_1, x_2, \cdots, x_{n+1}$を未知数とする連立方程式
$\begin{equation} \left\{ \, \begin{aligned} & x_1\sigma_1(u_1)+x_2\sigma_1(u_2)+\cdots +x_n\sigma_1(u_n)+x_{n+1}\sigma_{1}(u_{n+1})=0 \cdots ㋐\\ & x_1\sigma_2(u_2)+x_2\sigma_2(u_2)+\cdots +x_n\sigma_2(u_n)+x_{n+1}\sigma_{2}(u_{n+1})=0\cdots ㋑ \\ & \ldots \\ & x_1\sigma_n(u_1)+x_2\sigma_n(u_2)+\cdots +x_n\sigma_2(u_n)+x_{n+1}\sigma_{n}(u_{n+1})=0\cdots ㋒ \end{aligned} \right. \end{equation}$
を考える。
この連立方程式は式の数より文字の数の方が多いので、必ず非自明な解を持つ。
$x_1=a_1, x_2=a_2, \cdots, x_{n+1}=a_{n+1}$とすると、
$a_1, a_2, \cdots, a_{n+1} \in L$の少なくとも一つは$0$でないものが存在し、
$\begin{equation} \left\{ \, \begin{aligned} & a_1\sigma_1(u_1)+a_2\sigma_1(u_2)+\cdots +a_n\sigma_1(u_n)+a_{n+1}\sigma_{1}(u_{n+1})=0 \cdots ㋐\\ & a_1\sigma_2(u_2)+a_2\sigma_2(u_2)+\cdots +a_n\sigma_2(u_n)+a_{n+1}\sigma_{2}(u_{n+1})=0\cdots ㋑ \\ & \ldots \\ & a_1\sigma_n(u_1)+a_2\sigma_n(u_2)+\cdots +a_n\sigma_2(u_n)+a_{n+1}\sigma_{n}(u_{n+1})=0\cdots ㋒ \end{aligned} \right. \end{equation}$
が成立する。
$a_1, a_2, \cdots, a_{n+1}$は対等であるので、
$a_1 \neq 0$としても一般性を損なわない。
ゆえに以降では$a_1 \neq 0$とする。
また、補題より$n$個の異なる$Aut_K(L)$の元$\sigma_i$ $(i=1, 2, \cdots, n)$
に対して、
$\sigma_1(b)+\sigma_2(b)+\cdots +\sigma_n(b)\neq 0$
となる$b \in L$が存在する。
上記㋐㋑…㋒各式の両辺に$\dfrac{b}{a_1}$をかけ、
$r_i=\dfrac{b}{a_1}x_i$ $(i=1, 2, \cdots, n+1)$とすると、
$\begin{equation} \left\{ \, \begin{aligned} & \sigma_1(u_1)r_1+\sigma_1(u_2)r_2+\cdots +\sigma_1(u_n)r_n+\sigma_{1}(u_{n+1})r_{n+1}=0 \cdots ㋐\\ & \sigma_2(u_2)r_1+\sigma_2(u_2)r_2+\cdots +\sigma_2(u_n)r_n+\sigma_{2}(u_{n+1})r_{n+1}=0\cdots ㋑ \\ & \ldots \\ & \sigma_n(u_1)r_1+\sigma_n(u_2)r_2+\cdots +\sigma_2(u_n)r_n+\sigma_{n}(u_{n+1})r_{n+1}=0\cdots ㋒ \end{aligned} \right. \end{equation}$
となる。($b$を登場させたのは補題を使うための布石です)
$Aut_K(L)$は群なので、各$\sigma_i$には逆元$\sigma_i^{-1}$が存在する。
上記㋐㋑…㋒式の両辺に$\sigma_i^{-1}$を作用させると、
(補題を使うには\sigma \in Aut_K(L)を取ってきて$\sigma(b)$っぽい形が必要です。$\sigma_i^{-1} \in Aut_K(L)$なので無理やりその形に持ち込んでいます)
$\begin{equation} \left\{ \, \begin{aligned} & u_1\sigma_1^{-1}(r_1)+u_2\sigma_1^{-1}(r_2)+\cdots +u_n\sigma_1^{-1}(r_n)+u_1\sigma_{1}^{-1}(r_{n+1})=0 \cdots ㋐\\ & u_1\sigma_2^{-1}(r_1)+u_2\sigma_2^{-1}(r_2)+\cdots +u_n\sigma_2^{-1}(r_n)+u_1\sigma_{2}^{-1}(r_{n+1})=0 \cdots ㋑ \\ & \ldots \\ & u_1\sigma_n^{-1}(r_1)+u_2\sigma_n^{-1}(r_2)+\cdots +u_n\sigma_n^{-1}(r_n)+u_1\sigma_{n}^{-1}(r_{n+1})=0 \cdots ㋒ \end{aligned} \right. \end{equation}$
となる。
これらの式を全て足し合わせると、
$u_1\lbrace \sigma_1^{-1}(r_1)+\sigma_2^{-1}(r_1)+\cdots +\sigma_n^{-1}(r_1) \rbrace$
$+u_2\lbrace \sigma_1^{-1}(r_2)+\sigma_2^{-1}(r_2)+\cdots +\sigma_n^{-1}(r_2) \rbrace$
$+\cdots +u_{n+1}\lbrace \sigma_1^{-1}(r_{n+1})+\sigma_2^{-1}(r_{n+1})+\cdots +\sigma_n^{-1}(r_{n+1}) \rbrace=0$
となる。
定義より$r_i=\dfrac{b}{a_1}a_1=b$
であることと、
$\lbrace \sigma_1, \sigma_2, \cdots, \sigma_n \rbrace$
と
$\lbrace \sigma_1^{-1}, \sigma_2^{-1}, \cdots, \sigma_{n}^{-1}\rbrace$
が集合として等しいこと、
更に補題を合わせると、
$\sigma_1^{-1}(r_1)+\sigma_2^{-1}(r_1)+\cdots +\sigma_n^{-1}(r_1) \in K$
であり、かつ
$\sigma_1^{-1}(r_1)+\sigma_2^{-1}(r_1)+\cdots +\sigma_n^{-1}(r_1) \neq 0$
である。
以上のことから、$u_1, u_2, \cdots, u_{n+1}$は$K$上線形独立であることになり、
$[L:K]≦n$
となる。
$n=\mid Aut_K(L) \mid$
であったことと、$\mid Aut_k(L)≦[L:K]$
であることと合わせて、
$[L:K]≦\mid Aut_K(L) \mid ≦[L:K]$
となり、$[L:K]=\mid Aut_K(L) \mid$
が成立する。
よって、$L^G=K$のとき、$L/K$はガロア拡大である
(証明終了)
次は逆をいってみましょう!
ガロア拡大⇒固定体
(ガロア拡大⇒固定多)
$L/K$を有限次の体拡大とする。また、$G=Aut_K(L)$とする。
このとき、$L/K$がガロア拡大であるならば、$L^G=K$である
要するに$\mid Aut_K(L) \mid =[L:K]$という条件を使って$L^G=K$を示そう!という証明です。
示したいのは$L^G=K$です。$L^G$と$K$はともに集合で、集合が等しいことを示すので、
最もシンプルな発想で考えると$L^G \subset K$かつ$K \subset L^G$を示すことになります。
しかし今回$L^G$は$K$上の線形空間であると捉えることが可能なので、
体の拡大次数に関する定理が使えますので、これでショートカットしていきます。
(体の拡大次数に関する定理)
$K, M, L$を体とし、$K \subset M \subset L$とする。
このとき、$[L:K]=[L:M][M:K]$が成り立つ
これを駆使して証明をショートカットするための補題を示します。
(補題)
$K, M, L$を体とし、$K \subset M \subset L$とする。
このとき、$[L:M]=[L:K]$ならば、$M=K$が成り立つ
(補題の証明)
体の拡大次数に関する定理より、
$[L:K]=[L:M][M:K]$である。
ここで、条件より$[L:M]=[L:K]$であるので、
これを$[L:K]=[L:M][M:K]$に代入すると、
$[L:M]=[L:M][M:K]$
となり、$[M:K]=1$となる。
いま$K \subset M$であるので、
$K$上の線形空間$M$の基底は一つである。
$M$は体なので必ず$1$を含む。そこで、$1$を基底としてとると、
よって、$M=\lbrace a×1 \mid a \in K \rbrace$…①
である。$a×1=a \in K$なので、①が意味するところは$M=K$である。
(証明終了)
線形空間という言葉に馴染みのない方や、体の拡大次数に関する定理の証明が気になる方は
以下の記事をご覧ください。

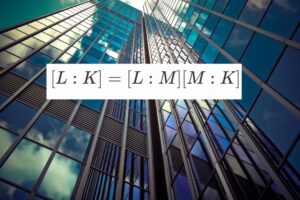
では証明いってみましょう!!
ガロア拡大⇒固定体の証明
(ガロア拡大⇒固定多)
$L/K$を有限次の体拡大とする。また、$G=Aut_K(L)$とする。
このとき、$L/K$がガロア拡大であるならば、$L^G=K$である
(証明)
$L^G$の定義より、$K\subset L^G \subset L$である。
いま、$[L:L^G]$と$[L:K]$について、
$[L:L^G]=[L:K]$を示すことができれば補題より$L^G=K$を導くことができる。
まず$[L:L^G]$について考える。
$G=Aut_K(L) \subset Aut(L)$である。
ここで、体の拡大$L/L^G$について、
$L$の$G$による固定体は$L^G$であるので、
定理「固定体⇒ガロア拡大」において$K$を$L^G$に置き換えて考えると、
$L/L^G$はガロア拡大となり、$[L:L^G]=\mid G \mid$
となる。
次に$L:K$を考える。
条件より$L/K$がガロア拡大なので、
$[L:K]=\mid Aut_K(L) \mid =\mid G \mid$である。
したがって$[L:L^G]=[L:K]$となり、補題より
$L^G=K$が示される
(証明終了)
まとめ
いかがでしたか?
・固定体⇒ガロア拡大
・ガロア拡大⇒固定体
・ゆえにガロア拡大⇔固定体
いままでガロア拡大の定義は$[L:K]=\mid Aut_K(L) \mid$
だったが、$[L:K]=\mid Aut_K(L) \mid$と$K=L^G$は同値であるため、
ガロア拡大の定義として$K=L^G$を採用してもよい、
という流れを押さえていただければと思います。
次回はまた違ったガロア拡大の同値表現を扱っていきたいと思います。
ご期待ください。
参考
[1] エミール・アルティン, ガロア理論入門, 筑摩書房, 2010
[2] 中島匠一, 代数方程式とガロア理論, 共立出版, 2006

コメント