今回は第三同型定理を扱います。
第三同型定理を端的に言い表すと、
分数の割り算と似たようなことが群でも成り立つ、という感じになります。
すごく美しいこの性質を証明していきます。
今回は具体例の計算をかなり重視しました。
なぜなら定理の内容を深くするには具体例で実感をもつことが非常に大切だからです。
面倒な計算がめっちゃ続いていますが、その分納得感は高いと思いますので、
そのつもりで読み進めていただければと思います。
第三同型定理の主張
まずは定理の主張を確認しましょう。
(第三同型定理)
$G$を群都とし、$H, N$は$G$は正規部分群であるとする。
更に$N \subset H$である。
このとき、
$(G/N)/(H/N) \cong G/H$
が成り立つ。
どうですか?めっちゃヤバくないですか?
例えば、我々は小学5年生で分数の割り算を習います。
$\dfrac{5}{7} ÷\dfrac{4}{7}=\dfrac{5}{7}×\dfrac{7}{4}$
$=\dfrac{5}{4}$
これと似たようなことが群でも成り立つ
というのが第三同型定理の主張です。
すごいことです。
初めてこの定理を見たときは
ま、マジかよ!!
群でも約分っぽいことできるのかよ!
と大興奮しました。
次は具体例を見ていこうと思います。
第三同型定理を扱うにあたっては、
以下の知識が基礎となりますので、馴染みのない方は是非ご覧ください。
・剰余類・剰余群について

・正規部分群について

・準同型写像について

・像と核について

・準同型定理(第一同型定理)について
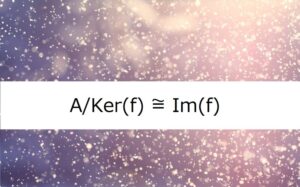
準同型定理の具体例
ここでは、第三同型定理の具体例を見ていきます。
その前に、もう一度主張を確認しておきましょう。
(第三同型定理)
$G$を群都とし、$H, N$は$G$は正規部分群であるとする。
更に$N \subset H$である。
このとき、
$(G/N)/(H/N) \cong G/H$
が成り立つ
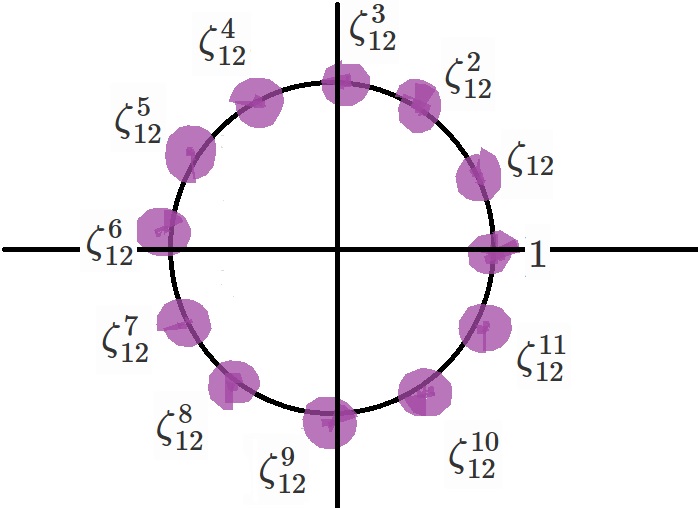
今回の具体例は、1の12乗根で考えていこうと思います。
$\zeta_{12}$を1の12乗根とします。
具体的に書き下すと、
$\zeta_{12}= \cos \dfrac{2\pi}{12}+i \sin \dfrac{2\pi}{12}$
です。
$G=\lbrace 1, \zeta_{12}, \zeta_{12}^2, \zeta_{12}^3, \zeta_{12}^4, \zeta_{12}^5, \zeta_{12}^6, \zeta_{12}^7, \zeta_{12}^8, \zeta_{12}^9, \zeta_{12}^{10}, \zeta_{12}^{11}\rbrace$
としましょう。
複素数平面上に$G$の元を図示すると、以下のように正12角形ができあがります。
するとこれは掛け算×に関して群となります。
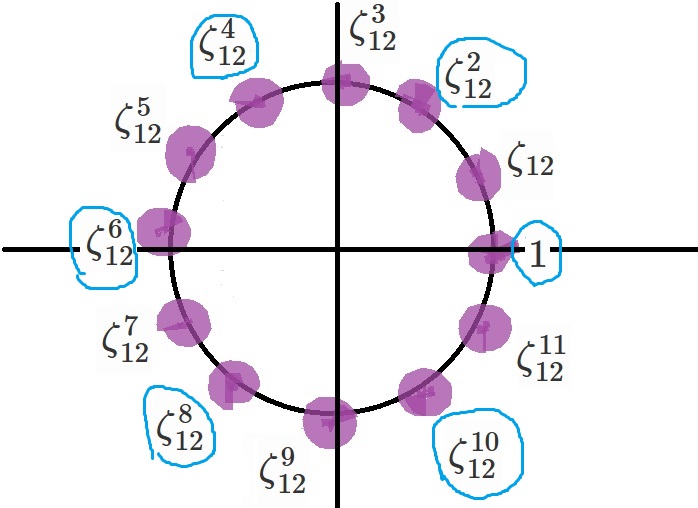
また、
$H=\lbrace 1, \zeta_{12}^2, \zeta_{12}^4, \zeta_{12}^6, \zeta_{12}^8, \zeta_{12}^{10}\rbrace $
とします。
これは複素数平面上では正六角形になります。
さらに
$N=\lbrace 1, \zeta_{12}^4, \zeta_{12}^8 \rbrace $
としましょう。
これは複素数平面上で正三角形となります。
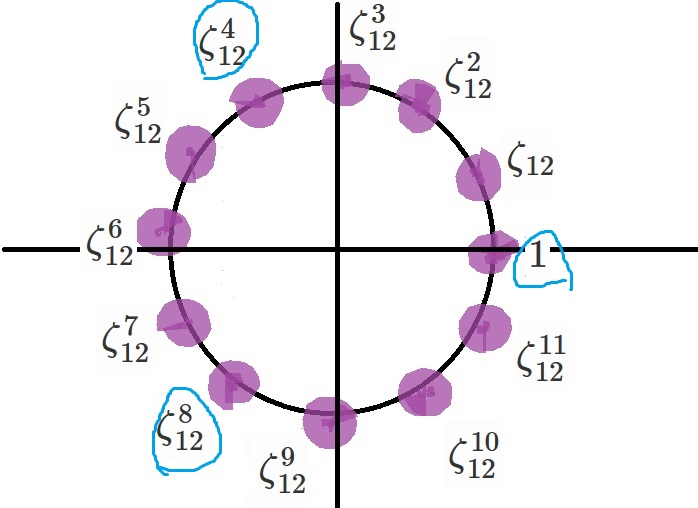
$N \subset H$は見たまんまですね。
×は交換法則を満たすので、$H$と$N$は$G$の正規部分群となります。
正規部分群の性質から、
$G/N$と$H/N$と$G/H$はそれぞれ剰余群となります。
こいつらを具体的に見ていきましょう。
$G/N$について、定義から順番に考えていきましょう。
定義通り考えると、
$G/N=\lbrace g〇N \mid g \in G \rbrace$
です。今回は×についての群なので、演算は〇ではなく×です。
×記号は省略することが多いので、今回は省略して書こうと思います。
$G/N=$
$\lbrace N, \zeta_{12}N, \zeta_{12}^2N, \zeta_{12}^3N, \zeta_{12}^4N, \zeta_{12}^5N, \zeta_{12}^6N, \zeta_{12}^7N, \zeta_{12}^8N, \zeta_{12}^9N, \zeta_{12}^{10}N, \zeta_{12}^{11}N \rbrace$
ここで、
$N=\lbrace 1, \zeta_{12}^4, \zeta_{12}^8 \rbrace $
$\zeta_{12}N=\lbrace \zeta_{12}, \zeta_{12}^5, \zeta_{12}^9 \rbrace $
$\zeta_{12}^2N=\lbrace \zeta_{12}^2, \zeta_{12}^6, \zeta_{12}^{10} \rbrace $
$\zeta_{12}^3N=\lbrace \zeta_{12}^3, \zeta_{12}^7, \zeta_{12}^{11} \rbrace $
$\zeta_{12}^4N=\lbrace \zeta_{12}^4, \zeta_{12}^8, \zeta_{12}^{12}(=1) \rbrace $
したがって、
$\zeta_{12}^4N=N$
となり、同様に
$\zeta_{12}^5N=\zeta_{12}N$
$\zeta_{12}^6N=\zeta_{12}^2N$
$\zeta_{12}^7N=\zeta_{12}^3N$
$\zeta_{12}^8N=\zeta_{12}^4N=N$
$\zeta_{12}^9N=\zeta_{12}^2N$
$\zeta_{12}^{10}N=\zeta_{12}^3N$
$\zeta_{12}^{11}N=N$
と分かります。
よって、
$G/N=\lbrace N, \zeta_{12}N, \zeta_{12}^2N, \zeta_{12}^3N \rbrace$
となります。
同様にして考えると、定義より
$H/N=\lbrace N, \zeta_{12}^2N, \zeta_{12}^4N, \zeta_{12}^6N, \zeta_{12}^8N, \zeta_{12}^{10}N \rbrace$
です。
$N=\lbrace 1, \zeta_{12}^4, \zeta_{12}^8 \rbrace $
$\zeta_{12}^2N=\lbrace \zeta_{12}^2, \zeta_{12}^6, \zeta_{12}^{10}\rbrace$
$\zeta_{12}^4N=\lbrace \zeta_{12}^4, \zeta_{12}^8, \zeta_{12}^{12}(=1)\rbrace=N$
$\zeta_{12}^8N=\zeta_{12}^2N$
$\zeta_{12}^{10}=\zeta_{12}^4N=N$
となるので、
$H/N=\lbrace N, \zeta_{12}^2N \rbrace$
となります。
$G/N=\lbrace N, \zeta_{12}N, \zeta_{12}^2N, \zeta_{12}^3N \rbrace$
と
$H/N=\lbrace N, \zeta_{12}^2N \rbrace$
から$(G/N)/(H/N)$を考えていきましょう。
定義から、
$(G/N)/(H/N)=\lbrace x (H/N)\mid x \in G/N \rbrace$
となります。
$x=N, \zeta_{12}N, \zeta_{12}^2N, \zeta_{12}^3N$
を踏まえて計算していくと、
$(G/N)/(H/N)=\lbrace H/N, \zeta_{12}(H/N), \zeta_{12}^2(H/N), \zeta_{12}^3(H/N) \rbrace$
となります。
ここで、
$H/N=\lbrace N, \zeta_{12}^2N \rbrace$
$\zeta_{12}(H/N)=\lbrace \zeta_{12}N, \zeta_{12}^3N \rbrace$
$\zeta_{12}^2(H/N)=\lbrace \zeta_{12}^2N, \zeta_{12}^4N \rbrace $
$\zeta_{12}^3(H/N)=\lbrace \zeta_{12}^3N, \zeta_{12}^5N \rbrace$
です。
ここで、$\zeta_{12}^4N=N$であったことを思い出しましょう。
すると、
$\zeta_{12}^2(H/N)=\lbrace \zeta_{12}^2N, \zeta_{12}^4N \rbrace $
$=\lbrace \zeta_{12}^2N, N \rbrace$
$=H/N$
となります。
また、
$\zeta_{12}^3(H/N)=\lbrace \zeta_{12}^3N, \zeta_{12}^5N \rbrace$
$=\lbrace \zeta_{12}^3N, \zeta_{12}N \rbrace$
$=\zeta_{12}(H/N)$
となります。以上のことから、
$(G/N)/(H/N)=\lbrace H/N, \zeta_{12}(H/N)\rbrace$
と分かります。
一方、$G/H$はどうでしょうか?
これも定義から考えていきましょう。
$G/H=$
$\lbrace H, \zeta_{12}H, \zeta_{12}^2H, \zeta_{12}^3H, \zeta_{12}^4H, \zeta_{12}^5H, \zeta_{12}^6H, \zeta_{12}^7H, \zeta_{12}^8H, \zeta_{12}^9H, \zeta_{12}^{10}H, \zeta_{12}^{11}H\rbrace$
となります。
ここで、
$H=\lbrace 1, \zeta_{12}^2, \zeta_{12}^4, \zeta_{12}^6, \zeta_{12}^8, \zeta_{12}^{10}\rbrace $
$\zeta_{12}H=\lbrace \zeta_{12}, \zeta_{12}^3, \zeta_{12}^5, \zeta_{12}^7, \zeta_{12}^9, \zeta_{12}^{11}\rbrace $
$\zeta_{12}^2H=\lbrace \zeta_{12}^2, \zeta_{12}^4, \zeta_{12}^6, \zeta_{12}^8, \zeta_{12}^{10}, \zeta_{12}^{12}(=1)\rbrace =H$
よって、
$\zeta_{12}^3H=\zeta_{12}H$
$\zeta_{12}^4H=H$
$\zeta_{12}^5H=\zeta_{12}H$
$\zeta_{12}^6H=H$
$\zeta_{12}^7H=\zeta_{12}H$
$\zeta_{12}^8H=H$
$\zeta_{12}^9H=\zeta_{12}H$
$\zeta_{12}^{10}H=H$
$\zeta_{12}^{11}H=\zeta_{12}H$
$\zeta_{12}^5H=\zeta_{12}H$
です。
したがって、
$G/H=\lbrace H, \zeta_{12}H \rbrace$
となります。
$(G/N)/(H/N)=\lbrace H/N, \zeta_{12}(H/N)\rbrace$
と
$G/H=\lbrace H, \zeta_{12}H \rbrace$
を比べてみると、確かにこれは同型っぽいですね!
具体的には、
$f(x (H/N))=xH$
という写像を定めれば、これが同型写像になります。
さて、第三同型定理のイメージが何となく固まってきたところで、
証明に進んでいきましょう。
第三同型定理の証明
(第三同型定理)
$G$を群とし、$H, N$は$G$は正規部分群であるとする。
更に$N \subset H$である。
このとき、
$(G/N)/(H/N) \cong G/H$
が成り立つ。
剰余群+同型=準同型定理で証明
という発想でいきます。
準同型定理の内容を確認しておきましょう
(準同型定理)
群$A$から群$B$への準同型写像を$f$とする。
このとき、$A/Ker(f) \cong Im(f)$
が成り立つ。
準同型写像$f$さえ上手く定めることができれば、
準同型定理によって全自動で同型をゲットすることができます。
準同型定理マジで便利ですよね!
では、証明をしていこうと思います!
(第三同型定理の証明)
$(G/N)/(H/N) \cong G/H$を示す。
$G/N$から$G/H$への写像$f$を次のように定める。
$x \in G/N$について、
$f(xN)=xH$
すると、$f$は$G/N$から$G/H$への準同型写像となる。
準同型定理より、
$(G/N)/Ker(f) \cong Im(f)$
である。
ここで、像の定義より、
$Im(f)=\lbrace f(xN) \mid xN \in G/N \rbrace$
である。
$f(xN)=xH$
より、
$Im(f)=\lbrace xH \mid xN \in G/N \rbrace$
$=\lbrace xH \mid x \in G \rbrace$
$=G/H$
したがって、
$Im(f)=G/H$…①
また、核の定義より、
$Ker(f)=\lbrace xN \mid f(xN)=H \rbrace$
$=\lbrace xN \mid x \in H \rbrace$
$=H/N$
したがって、
$Ker(f)=H/N$…②
$(G/N)/Ker(f) \cong Im(f)$
に①②を代入すると、
$(G/N)/(H/N) \cong G/H$
が成立する。
(証明終了)
証明自体は結構シンプルですね
まとめ
いかがだったでしょうか?
・第三同型定理は分数の割り算的なことが群でもできるということを主張している
・証明では準同型定理(第一同型定理)を用いる
・準同型定理マジで便利
以上を押さえていただければと思います。
ではまた次回の記事でお会いしましょう!
参考
画像素材提供(アイキャッチ):Ronny OverhateによるPixabayからの画像

コメント