ガロア理論に古典的にアプローチしていくと、
体の拡大次数と剰余群の位数について神秘的な対応関係を発見することになります。
体と群。
この2つの概念を結びつける道具が、体の同型写像(自己同型写像)です。
今回の記事では、体の同型写像が解の置換を引き起こす点について詳しく解説していきたいと思います。
体と群の対応関係
まずはこれまでのおさらいからいきましょう。
方程式についてです。
方程式を解くとは、係数の世界を広げることでした。
例えば、$x^2-3=0$は有理数係数の方程式です。
有理数係数$\mathbb{Q}$の範囲では、$x^2-3=0$はこれ以上因数分解できないので、解くことができません。
しかし、これを$\mathbb{Q}(\sqrt{3})$の世界まで広げると、
$x^2-3=(x-\sqrt{3})(x+\sqrt{3})$と因数分解することができ、
解くことができます。
ひとまず$x^2-3=0$が解けることは分かりましたが、
他の方程式はどうでしょう?
2次方程式には解の公式があります。
3次方程式にも解の公式があります。
4次方程式にも解の公式があります。
でも、5次以上の方程式には解の公式がありません。
$x^5-1=0$のような方程式は解けますが、大部分の5次方程式は解くことができないのです。
では、解ける方程式と、解けない方程式は何が違うのでしょう?
解ける方程式と、解けない方程式を比べると、圧倒的に解ける方程式の方が少ないので、
まずは解ける方程式の具体例を観察しました。
その際に大活躍したのが、「解と係数の関係」と「対称式の基本定理」のコンボ技。
対称式を作ることができれば、対称式の機本体定理より、それを基本対称式で表すことができます。
さらに、解と係数の関係より、基本対称式は全てもとの方程式の係数の四則演算で表されます。
すると、結果的に解の対称式がもとの方程式の係数で表されることになり、解けます。
ここで画期的だったのは、「方程式を解く」という過程で「対称式をいかにして手に入れるか」
ということが重要になっていった点です。
対称性を調べるために、人類は「群」、とくに並び替えの群である「置換群」を発明したのです。
ここで、体を拡大する作業と、置換群の剰余群を調べる作業には、神秘的な対応関係があるのでした。
例えば、3次方程式の場合は以下のような結果となります。

詳しくは↓の記事をご覧ください。

注目すべきは、緑の文字のところです!
まず左側の体(たい)の世界の緑の文字を見てください。
緑色で「2乗根」、「3乗根」と書かれているのが分かると思います。
この「2乗根」と「3乗根」は、体の言葉で表現すると、「拡大次数」を表しています。
体の拡大次数についての詳しい内容は、以下の記事をご覧ください。
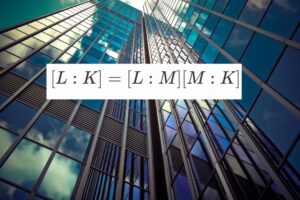
要するに、体の世界をどのくらい広げたかを表していると持ってください。
一方で、リゾルベントを不変に保つ並び替えにも緑の数がかかれています。
「6÷3=2」と「3÷1=3」は、剰余群の位数を表しています。
そう、「体の拡大次数」と「剰余群の位数」が一致しているのです!
要するに、方程式の係数(体の世界)と並び替え(群の世界)の橋渡しをしてくれるような道具が必要になります。
これを上手く数学的に記述するために、「体の自己同型写像」が活躍するのです!
では、先に進んでいきましょう。
体の同型写像と自己同型写像
次に道具の定義を確認しておきましょう。
体は、簡略のためひとまず四則演算で閉じた集合と解釈していきます。
定義の確認
(体の同型写像の定義)
$F_1$と$F_2$を体とする。
写像$f: F_1$ $→$ $F_2$
が全単射で、かつ
$a, b \in F_1$に対して
$f(a+b)=f(a)+f(b)$
$f(ab)=f(a)f(b)$
を満たすとき、$f$を体の同型写像という。
$F_1, F_2$に対して体の同型写像が存在するとき、
$F_1$と$F_2$は同型であるといい、
$F_1 \cong F_2$と表す
つづいて、今回の記事の主役、自己同型写像です。
(体の自己同型写像の定義)
体$F$から体$F$自身への同型写像を、
自己同型写像という
体$F$の自己同型写像全体からなる集合を、$Aut (F)$と表す
そしてなんと、$Aut (F)$は群をなすのです!!
自己同型写像全体からなる集合は群をなす
(定理:$Aut (F)$は群をなす)
$F$を体とする。このとき、$Aut (F)$は写像の合成$〇$について群をなす
($Aut (F)$が群をなすことの証明)
まず、$Aut (F)$が写像の合成$〇$について閉じていることを確認する。
$\sigma_1, \sigma_2 \in Aut(F)$について、
$\sigma_1 〇 \sigma_2 \in Aut (F)$であればよい。
$x, y \in F$について考える。
$\sigma_1〇\sigma_2(x+y)=\sigma_1 \lbrace \sigma_2(x+y) \rbrace$
$=\sigma_1\lbrace \sigma_2(x)+\sigma_2(y) \rbrace$
$=\sigma_1\lbrace \sigma_2(x)\rbrace + \sigma_1\lbrace \sigma_2(y)\rbrace$
$=\sigma_1 〇 \sigma_2(x)+\sigma_1 〇 \sigma_2(y)$…①
また、
$\sigma_1〇\sigma_2(xy)=\sigma_1 \lbrace \sigma_2(xy) \rbrace$
$=\sigma_1\lbrace \sigma_2(x)\sigma_2(y) \rbrace$
$=\sigma_1\lbrace \sigma_1(x)\rbrace \sigma_1\lbrace \sigma_1(y)\rbrace$
$=\sigma_1 〇 \sigma_2(x)\sigma_1 〇 \sigma_2(y)$…②
である。なお、$\sigma_1, \sigma_2$は全単射であるので、$\sigma_1〇\sigma_2$も全単射である。
①②より、$\sigma_1〇\sigma_2$もまた$F$の自己同型写像となるため、
$Aut (F)$は写像の合成に関して閉じていることが確認された…㋐
次に、単位元が存在することを確認する。
$e:F$ $→$ $F$
を恒等写像とする。すなわち、$x \in F$に対して、$e(x)=x$である。
$x, y \in F$に対して
$e(x+y)=x+y=e(x)+e(y)$
であり、
$e(xy)=xy=e(x)e(y)$
である。
よって、$e \in Aut(F)$である。
ここで、$\sigma \in Aut(F)$に対して
$e〇\sigma(x)=\sigma(x)$
$\sigma(x)〇e(x)=\sigma(x)$
であるので、$e$は$Aut (F)$の単位元となる…㋑
次に、$Aut (F)$が結合法則と満たすことを示す。
$\sigma_1, \sigma_2, \sigma_3 \in Aut (F)$に対して、
$\sigma_1〇(\sigma_2 〇 \sigma_3)=(\sigma_1 〇 \sigma_2)〇\sigma_3$
であればよい。
$x \in F$について、
$\sigma_1〇(\sigma_2 〇 \sigma_3)(x)=\sigma_1(\sigma_2(\sigma_3(x)))$
$(\sigma_1 〇 \sigma_2)〇\sigma_3=\sigma_1(\sigma_2(\sigma_3(x)))$
であるので、
$\sigma_1〇(\sigma_2 〇 \sigma_3)=(\sigma_1 〇 \sigma_2)〇\sigma_3$
であり、結合法則は成立する…㋒
最後に逆元が存在することを確認する。
$\sigma \in Aut (F)$について、$\sigma^{-1} \in Aut(F)$であればよい。
いま、$\sigma: F$ $→$ $F$
を考える。$\sigma$は全単射であるので、
$x \in F$にたいして、sigma(x)=a$となる$a \in F$がただ一つ存在する。
$x$から$a$への対応はただ1通りであるので、逆に$a$から$x$への対応もただ1通りに定まる。
これを$\sigma^{-1}$と表すことにする。すなわち、
$\sigma^{-1}(a)=x$である。
$\sigma^{-1} \in Aut (F)$を確認する。
$\sigma$が全単射であるので、$\sigma^{-1}$もまた全単射である。
$\sigma^{-1}(\sigma(x))=\sigma^{-1}(a)=x$
であるので、$\sigma^{-1}〇\sigma=e$である。
同様に、$\sigma〇\sigma^{-1}=e$である。
いま、$x, y, a, b \in F$について、
$\sigma(x)=a, \sigma^{-1}(a)=x, \sigma(y)=b, \sigma^{-1}(b)=y$とする。
$\sigma(x+y)=\sigma(x)+\sigma(y)$
$=a+b$
よって、$\sigma(x+y)=a+b$であり、
$\sigma^{-1}〇\sigma(x+y)=\sigma^{-1}(a+b)$
$x+y=\sigma^{-1}(a+b)$
$\sigma^{-1}(a)+\sigma^{-1}(b)=\sigma^{-1}(a+b)$
よって、$\sigma^{-1}(a+b)=\sigma^{-1}(a)+\sigma^{-1}(b)$
同様に、
$\sigma(xy)=ab$
$\sigma^{-1}〇\sigma(xy)=\sigma^{-1}(ab)$
$xy=\sigma^{-1}(ab)$
$\sigma^{-1}(a)\sigma^{-1}(b)=\sigma^{-1}(ab)$
よって、$\sigma^{-1}(ab)=\sigma^{-1}(a)\sigma^{-1}(b)$
したがって、$\sigma^{-1} \in Aut (F)$…㋓
㋐㋑㋒㋓より、$Aut (F)$は写像の合成〇に関して群となる
(証明終了)
$Aut (F)$は群となるので、$Aut (F)$を自己同型群と呼びます。
そして最後に、$K$上の自己同型という概念が登場します。
K上の自己同型
($L$の$K$上の自己同型の定義)
$L/K$を体の拡大とする。体$L$の自己同型写像で、$K$の元を不変に保つものを、
$L$の$K$上の自己同型という。
$L$の$K$上の自己同型全体の集合を$Aut_K(L)$と表す
はい。この$Aut_K(L)$こそがガロア理論最高のギミックです。
次回以降の記事で大活躍しますので、ご期待ください。
同型写像と解の置換について
ここで紹介する定理が体の同型写像を考える意義といっても言い過ぎではないと思います。
もともとのモチベーションとして、ガロア理論で「体の拡大と並べ替えを紐づける道具が欲しい」
というものがありました。今から紹介する定理でその道具が体の同型写像であることが分かります。
(定理:自己同型で飛ばしたものもまた解になる)
$L/K$を体の拡大とする。
また、$\sigma \in Aut_K(L)$とし、
$f(x)$を、$K$を係数体とする$n$次多項式とする。
さらに、$f(x)=0$の解の一つを$\alpha$とし、
$\alpha \in L$でああるとする。
このとき、
$\sigma(\alpha)$もまた$f(x)=0$の解となる
証明は比較的簡単ですが、
体の同型写像が四則演算を保存することと、
$\sigma (0)=0$を使うので、
これらの詳細が気になる方は以下の記事をご覧ください。

では証明へ進んでいきましょう!
(自己同型で飛ばしたものもまた解になるの証明)
$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0$とおく。
$a_1, \cdots, a_n \in K$である。
$f(\alpha)=0$が成り立つときに$f(\sigma (\alpha))=0$であることを示せばよい。
$\sigma \in Aut_K(L)$について、
$f(\alpha)=0$より、
$a_n \alpha^n +a_{n-1}\alpha^{n-1}+\cdots +a_1\alpha +a_0=0$
である。よって、
$\sigma(a_n \alpha^n +a_{n-1}\alpha^{n-1}+\cdots +a_1\alpha +a_0)=\sigma(0)$
となる。$\sigma$は四則演算を保存することと、$\sigma(0)=0$より、
$\sigma(a_n)\lbrace \sigma(\alpha) \rbrace^n+\cdots \sigma(a_1)\sigma(\alpha)+\sigma(a_0)=0$
である。ここで、$\sigma \in Aut_K(L)$であり、$\sigma$は$K$の元を不変に保つので、
$a_n\lbrace \sigma(\alpha) \rbrace^n +\cdots +a_1 \sigma(\alpha)+a_0=0$
$f(\sigma(\alpha))=0$
よって、$\sigma(\alpha)$もまた$f(x)=0$の解となることが示された。
(証明終了)
この定理が何を意味するかを少し掘り下げていきましょう。
今回の定理では一般の体$K$を係数に取りましたが、
方程式を考えるときは普通は係数を有理数$\mathbb{Q}$にとるので、
以下では$f(x)$を$\mathbb{Q}$上の既約多項式としようと思います。
$f(x)=0$は$n$次方程式とします。
既約多項式の性質5つ目より、$f(x)=0$は重解を持ちません
(証明は以下の記事をご覧ください)

例えば、$n$次方程式$f(x)=0$の解を
$\alpha_1, \alpha_2, \cdot, \alpha_n$
とします。これらは全て異なるわけです。
ここで、先ほど示した定理より、
$\sigma(\alpha_1), \sigma(\alpha_2), \cdots, \sigma(\alpha_n)$も
また$f(x)=0$の解です。
$\sigma$は全単射なので、異なる2つの解の移り先は必ず異なる2つの解をなります。
要するに、
$\lbrace \alpha_1, \alpha_2, \cdots, \alpha_n \rbrace$
と
$\lbrace \sigma(\alpha_1), \sigma(\alpha_2), \cdots, \sigma( \alpha_n) \rbrace$
は集合としては等しく、違いは要素の順序のみ。
要するに、$\sigma$によって解の置換が引き起こされている、というわけです。
以上のことから、体の同型写像こそが、「体の拡大」と「解の並べ替え」をつなぎ合わせるものだと分かりました。
まとめ
いかがでいたか?
・方程式を解くためには、「対称式の基本定理」と「解と係数の関係」のコンボが強力
・対称式を調べるうえで、方程式の解の置換が大切
・「方程式を解く」とは、係数の範囲を広げることであったため、「体の拡大」と「解の並べ替え」をつなぎ合わせる上手い道具が必要だった
・その最高の道具が体の同型写像であった!
以上を押さえていただければと思います。
ではまた次回の記事でお会いしましょう!
参考
画像素材提供(アイキャッチ):jacqueline macouによるPixabayからの画像

コメント
コメント一覧 (4件)
興味深く記事を読ませてもらっています。
以前からガロア理論を理解したいと思って関連する本を読んでいましたが、専門的な数学書は難しくすっきりと理解できずにいました。
ここでのじゅんさんの説明が、具体的で分かりやすく理解が進みました。ぜひガロア理論の解説を最後まで続けていただければと思います。
次回の更新を楽しみにしています。
長谷川さん
嬉しいコメントありがとうございます。
長谷川さんのコメントに大変励まされたとともに
記事を書いていく元気をもらえました。
最近更新が滞っていますが、ガロア理論の解説は
今後も続けていきますので、ご期待ください!
勉強させていただいています。ありがとうございます。
私の勘違いだったらすみません。
K上の自己同型写像、の説明のところの2行め、「体Kの自己同型写像で」とあるのは、「体Lの自己同型写像で」ではないでしょうか?
数学徒Aさん
コメントありがとうございます!
その通りですね。
「体Kの自己同型写像で」→「体Lの自己同型写像で」が正しいです。
記事の方を訂正してまいりました。
ありがとうございました。
今後もよろしくお願いいたします!