群論を学ぶ上で一つのピークとなるのが準同型定理です。
でもこれって、どんな定理で、何が便利なのでしょう?
数式を見ているだけだと準同型定理の便利さやすごさは見えにくいものです。
そこで、今回の記事では具体例を通して準同型定理の意味と意義を確認していこうと思います。
準同型定理の主張と基礎事項の確認
まずは今回の主役、準同型定理のステートメントを確認しておこうと思います。
(準同型定理)
群$A$から群$B$への準同型写像を$f$とする。
このとき、$A/Ker(f) \cong Im(f)$
が成り立つ。
$A/Ker(f) \cong Im(f)$
という式がこの定理の主役です。
準同型定理の意味を理解するには、
① 準同型写像と$\cong$という記号の意味
② 剰余群
③ $Im(f)$ と $Ker(f)$
についての知識が必要となります。
順に確認しておきましょう。
①準同型写像
簡単に言うと、準同型写像は、ある群と別の群が似ているかどうかを判別する写像です。
(準同型写像の定義)
$G_1$を演算$*$についての群とし、
と$G_2$を演算〇についての群とする。
このとき、
写像$f:G_1$ $→$ $G_2$
が
$a, b \in G_1$ ⇒ $f(a*b)=f(a)〇f(b)$
を満たすとき、$f$を群の準同型写像という。
さらに、準同型写像が全単射の時、それを同型写像と言います。
(群の同型写像の定義)
$G_1$を演算$*$についての群とし、
と$G_2$を演算〇についての群とする。
このとき、
写像$f:G_1$ $→$ $G_2$
が
$a, b \in G_1$ ⇒ $f(a*b)=f(a)〇f(b)$
を満たし、更に全単射であるとき、
$f$を群の同型写像という。
なお、このとき$G_1$と$G_2$は同型であるといい、
$G_1\cong G_2$で表す。
準同型写像について、より詳しくは以下の記事をご覧ください。

②剰余群
剰余群を考えるにあたっては、まず剰余類について確認しておく必要があります。
剰余類とは、簡単に言えば
「出席番号順で3列に整列!」を一般化したものです。
群では可換法則が成立しないので、右から演算を施すか左から演算を施すかで
右剰余類、左剰余類と名前が変わります。
(左剰余類の定義)
群$G$と、その部分群$H$があり、$g \in G$をとる。
$\lbrace g〇h \mid h \in H \rbrace$
を$H$による$G$の左側剰余類といい、
$gH$で表す。
$H$による$G$の左剰余類を全てあつめた集合を
$G/H$で表します。
$G/H$の元は集合で、みな$gH$のような形をしていますから、
$G/H=\lbrace a〇H \mid a\in G\rbrace$
となります。
$G/H$が群になるとき、これを剰余群と言います。
剰余類、剰余群についての詳細は以下の記事をご覧ください。

③像と核
準同型定理に登場する記号$Im(f)$と$Ker(f)$を考えていきましょう。
$Im(f)$は像と言い、イメージ・エフと読みます。
$Ker(f)$は核と言い、カーネル・エフと読みます。
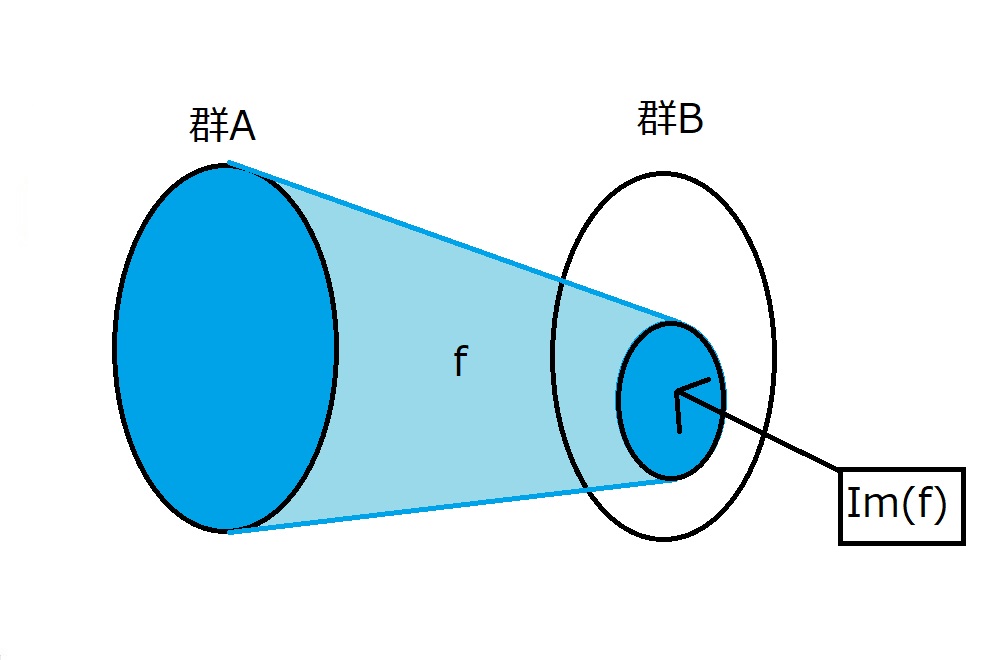
(像の定義)
群$A$から群$B$への準同型写像を$f$とする。
このとき、
$\lbrace f(a) \mid a \in A \rbrace$
を$f$の像といい、
$Im(f)=\lbrace f(a) \mid a \in A \rbrace$
で表す
図にすると以下のような感じになります。
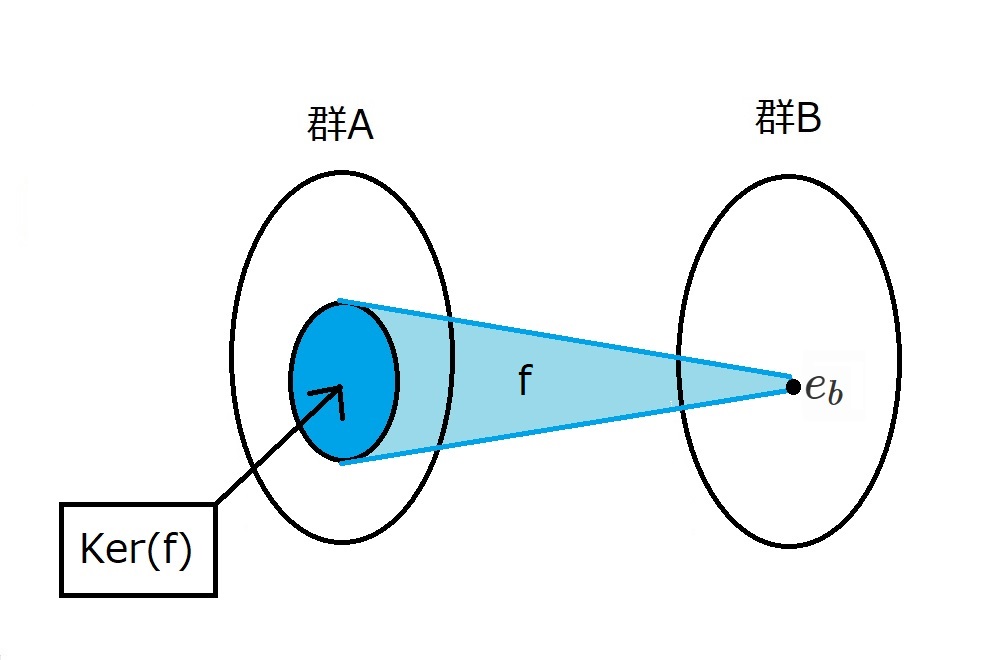
(核の定義)
群$A$から群$B$への準同型写像を$f$とする。
また、$B$の単位元を$e_b$とする。
このとき、
$\lbrace a \in A \mid f(a)=e_b \rbrace$
を$f$の核といい、
$Ker(f)=\lbrace a \in A \mid f(a)=e_b \rbrace$
で表す。
図にすると以下のような感じです。
像と核については、以下の4点の性質を押さえておきましょう。
群$A$から群$B$への準同型写像を$f$とします。このとき、
・$Im(f)$は$B$の部分群
・$Ker(f)$は$A$の正規部分群
・$Im(f)$は$f$が全射であることの判定に使える
・$Ker(f)$は$f$が単射であることの判定に使える
証明や詳細は以下の記事をご覧ください。

準同型定理の発想と具体例
準同型定理には
群$A$から群$B$への準同型写像$f$と、
像$Im(f)$と核$Ker(f)$が登場します。
$Im(f)$は$B$の部分群で、
$Ker(f)$は$A$の正規部分群です。
部分群よりも正規部分群の方が条件がきついので、
まずは正規部分群に着目しましょう。
正規部分群とはなにか?
その本質は、
剰余類を集めた集合が群になる、
という点に集約されます。
人類はそのために正規部分群という概念を生み出したのです。
詳しくはこちらの記事をご覧ください。

要するに、
正規部分群を発見したらとりあえず剰余群を観察してみる
という考え方が大切ということです。
ではここで一つ例を見てみましょう。
まず$\mathbb{Z}=\lbrace \cdots -3, -2, -1, 0, 1, 2, 3, \cdots \rbrace$
と$B=\lbrace 1, \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5 \rbrace$
を考えます。
$\mathbb{Z}$は足し算について群です。
また、$B$は掛け算について群です。
ここで、$\mathbb{Z}$から$B$への写像$f$を
$f(n)=\zeta_6^n$ $(n \in \mathbb{Z})$
とします。
すると、$s, t \in \mathbb{Z}$に対して、
$f(s+t)=\zeta_6^{s+t}$
$=\zeta_6^s〇\zeta_6^t$
$=f(s)〇f(t)$
となり、
$f(s+t)=f(s)〇f(t)$
が成り立つため、これは準同型写像です。
次にこの$f$に対して$Im(f)$と$Ker(f)$
を考えましょう。
まずは$Im(f)$から。
定義より、
$Im(f)=\lbrace f(n) \mid n \in \mathbb{Z} \rbrace$
です。
ここで、
$f(n)=\zeta_6^n$
でしたから、
$Im(f)=\lbrace \zeta_6^n \mid n \in \mathbb{Z} \rbrace$
となります。
$\zeta_6^6=1$に注意すると、結局これは
$Im(f)=\lbrace \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5, \zeta_6^6(=1) \rbrace$
となります。
$B=\lbrace 1, \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5 \rbrace$
でしたから、今回は
$Im(f)=B$
です。
さて、次は$Ker(f)$について考えていきましょう。
$B$の単位元は1なので、
定義より、
$Ker(f)=\lbrace n \in \mathbb{Z} \mid f(n)=1 \rbrace$
です。
$f(n)=\zeta_6^n$
なので、$f(n)=1$とすると、
$\zeta_6^n=1$
となる$n$を考えることになります。
$\zeta_6^6=1$
でした。他にも、
$\zeta_6^{12}=(\zeta_6^6)^2=1^2=1$
です。要するに、$n$が6の倍数(6で割った余りが0)であれば
$\zeta_6^n=1$
になります。したがって、
$Ker(f)=\lbrace n \in \mathbb{Z} \mid f(n)=1 \rbrace$
$=\lbrace n \in \mathbb{Z} \mid \zeta_6^n=1 \rbrace$
$=\lbrace 6m \mid m\in \mathbb{Z} \rbrace$
$=\lbrace \cdots, -18, -12, -6, 0, 6, 12, 18, \cdots \rbrace$
$=6\lbrace \cdots, -3, -2, -1, 0, 1, 2, 3, \cdots \rbrace$
$=6\mathbb{Z}$
つまり、
$Ker(f)=6\mathbb{Z}$
と分かりました。
$Ker(f)$は必ず$A$の正規部分群になっているので、剰余群を考えましょう。
今回は$A=\mathbb{Z}$なので、
$A/Ker(f)=\mathbb{Z}/6\mathbb{Z}$
です。
では$\mathbb{Z}/6\mathbb{Z}$とは何だったでしょうか?
これは剰余群なので、剰余群の定義を確認しましょう。
$G/H=\lbrace a〇H \mid a\in G\rbrace$
でした。
いま、$G=\mathbb{Z}$で、$H=6\mathbb{Z}$です。
さらに、$\mathbb{Z}$は足し算についての群なので、考えるべき演算は〇ではなく+です。
これを踏まえると、
$\mathbb{Z}/6\mathbb{Z}=\lbrace n+6\mathbb{Z} \mid n \in \mathbb{Z} \rbrace$
であると分かります。
具体的に書き下すと、
$\mathbb{Z}/6\mathbb{Z}$
$=\lbrace \cdots, 0+6\mathbb{Z}, 1+6\mathbb{Z}, 2+6\mathbb{Z}, 3+6\mathbb{Z}, $
$4+6\mathbb{Z}, 5+6\mathbb{Z}, 6+6\mathbb{Z}, 7+6\mathbb{Z}, \cdots \rbrace$
となります。
ここで、
$0+6\mathbb{Z}=6+6\mathbb{Z}=12+6\mathbb{Z}=\cdots $
$1+6\mathbb{Z}=7+6\mathbb{Z}=13+6\mathbb{Z}=\cdots $
$2+6\mathbb{Z}=8+6\mathbb{Z}=14+6\mathbb{Z}=\cdots $
$3+6\mathbb{Z}=9+6\mathbb{Z}=15+6\mathbb{Z}=\cdots $
$4+6\mathbb{Z}=10+6\mathbb{Z}=16+6\mathbb{Z}=\cdots $
$5+6\mathbb{Z}=11+6\mathbb{Z}=17+6\mathbb{Z}=\cdots $
ですので、まとめると
$\mathbb{Z}/6\mathbb{Z}=\lbrace 0+6\mathbb{Z}, 1+6\mathbb{Z}, 2+6\mathbb{Z}, $
$3+6\mathbb{Z}, 4+6\mathbb{Z}, 5+6\mathbb{Z} \rbrace$
となります。
$n+6\mathbb{Z}=\bar{n}$と表すことが多いので、これに習うと
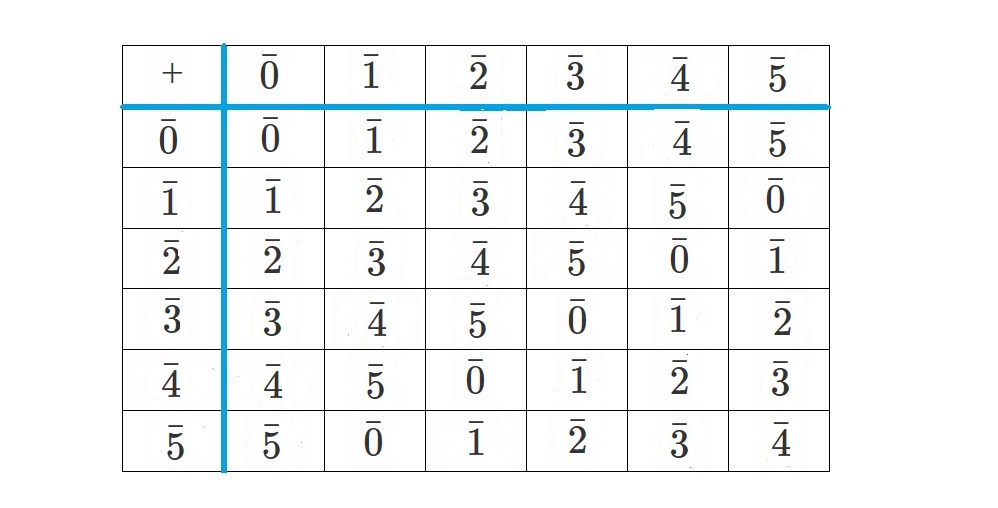
$\mathbb{Z}/6\mathbb{Z}=\lbrace \bar{0}, \bar{1}, \bar{2}, \bar{3}, \bar{4}, \bar{5} \rbrace$
となります。
剰余群について考える際には剰余類の知識が不可欠となるので、
読みにくい所もあるかもしれません。
剰余類に馴染みのない方は以下の記事をご覧ください。

さて。
ここで$\mathbb{Z}/6\mathbb{Z}$と$Im(f)$を比べてみましょう。
$\mathbb{Z}/6\mathbb{Z}$は足し算について群となり、演算表は以下です。
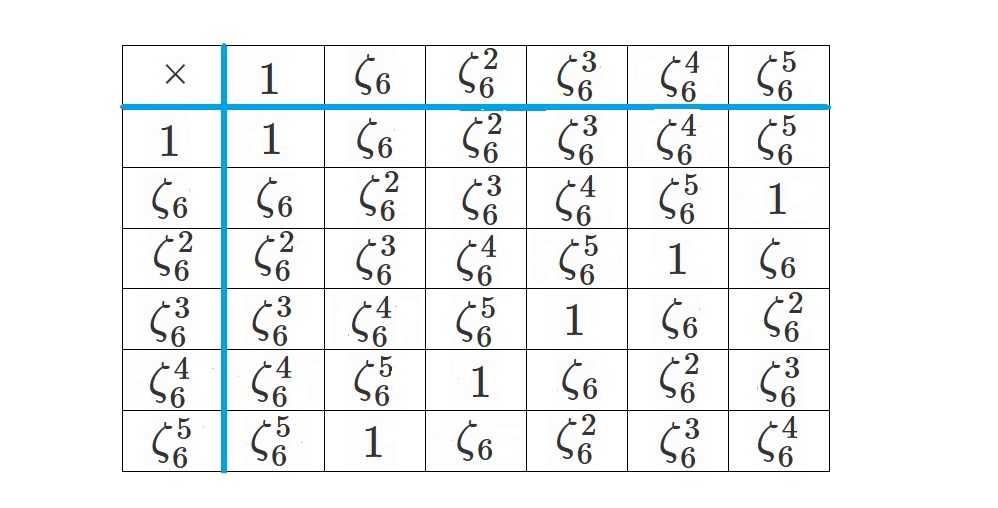
$Im(f)=\lbrace 1, \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5 \rbrace$
は掛け算について群であり、演算表は以下です。
どうですか?
こいつらかなり似てませんか?
$\mathbb{Z}/6\mathbb{Z}$と$Im(f)$の間には
$\bar{0}$ $→$ $1(=\zeta_6^0)$
$\bar{1}$ $→$ $\zeta_6$
$\bar{2}$ $→$ $\zeta_6^2$
$\bar{3}$ $→$ $\zeta_6^3$
$\bar{4}$ $→$ $\zeta_6^4$
$\bar{5}$ $→$ $\zeta_6^5$
という一対一対応があります。
この対応付けを$\bar{f}$と置くことにしましょう。
数式で表すと、$\bar{f}(\bar{n})=\zeta_6^n$
です。
すると、$\bar{f}$ は $\mathbb{Z}/6\mathbb{Z}$から $Im(f)$ への全単射となります。
つまり
$\mathbb{Z}/6\mathbb{Z}$と$Im(f)$は同型になっているのです!
これこそが準同型定理の主張となります。
ここまでの流れをまとめておくと、
①まず群$A$と群$B$が与えられる。
②$A$から$B$への準同型写像$f$を自分で定める
③すると、$f$によって$Im(f)$と$Ker(f)$が定まる
④$Ker(f)$は核なので、必ず$A$の正規部分群となるため、剰余群$A/Ker(f)$を考えることができる
⑤なんと$A/Ker(f)$から$Im(f)$への同型写像$\bar{f}$を作ることができる(しかも自動的に)
⑥そのため、$A/Ker(f) \cong Im(f)$となる
さて。
準同型定理って何が嬉しいのでしょうか?
それは、手順をよく見返してみると分かります。
①から⑥までの手順のうち、
自分で決めている部分は青マーカーの②だけ。
要するに準同型定理は、
準同型写像$f$を定めると、自動的に同型写像$\bar{f}$をゲットすることができるよ!
という定理なのです。
同型写像は全単射という条件を満たさなければならないので、
これをゼロから自分で考えるのは結構大変ですが、
準同型定理を使えば、同型写像より少し条件を緩めた準同型写像さえ作ればそれで同型写像をゲットできます。
これが準同型定理の嬉しいところです。
$f$と$\bar{f}$は違う写像である、と明確に意識しておくとよいでしょう。
それでは、証明へ進んでいきましょう!
準同型定理の証明
まずは準同型定理の主張を再確認しておきましょう。
(準同型定理)
群$A$から群$B$への準同型写像を$f$とする。
このとき、$A/Ker(f) \cong Im(f)$
が成り立つ。
要するに、$A$から$B$への準同型写像$f$を定めると、
$A/Ker(f)$から$Im(f)$への同型写像が作れるよ!ということを示せばよいです。
その同型写像を$\bar{f}$と置きましょう。
$\bar{f}$をどのように定めればよいでしょうか?
これは先ほどの例で確認した$\mathbb{Z}/6\mathbb{Z} \cong Im(f)$をベースに考えましょう。
先ほどの例では$A=\mathbb{Z}$として、
$B=\lbrace 1, \zeta_6, \zeta_6^2, \zeta_6^3, \zeta_6^4, \zeta_6^5 \rbrace$
と置いていました。
そして、$Ker(f)$を計算すると$6\mathbb{Z}$だったわけです。
$\mathbb{Z}/6\mathbb{Z} \cong Im(f)$
を確認する際には、$\bar{f}$を
$\bar{f}(\bar{n})=\zeta_6^n$と定義しました。
これを一般化しましょう。
これを考えるには、$\bar{n}$と$\zeta_6$を一般化させることが大切です。
まず、$\bar{n}$を考えましょう。
$\bar{n}=n+6\mathbb{Z}$
でした。ここで、$n \in \mathbb{Z}$です。
$\mathbb{Z}$は$A$で置き換えましょう。
また、$6\mathbb{Z}$は$Ker(f)$です。
そして、$+$は演算なので、$〇$としましょう。
要するに、$\bar{n}=n+6\mathbb{Z}$は
$a〇Ker(f)$ $(a \in A)$
と一般化されます。
では$\zeta_6^n$はどうでしょうか?
これは簡単です。
もともと$\mathbb{Z}$から$B$への準同型$f$を
$f(n)=\zeta_6^n$
で定めていたので、$f$の定義から
$\zeta_6^n=f(n)$です。
すると、$\bar{f}$は次のように考えることが可能です。
$\bar{f}(a〇Ker(f))=f(a)$
これを踏まえて準同型定理の証明の方針を考えていきましょう!
準同型定理で最終的に示したいのは
$A/Ker(f) \cong Im(f)$
です。このためには、
$A/Ker(f)$から$Im(f)$への写像$\bar{f}$が同型写像であることを示せばよいです。
ここで、$\bar{f}$は前提条件で与えられたものではなくて、自分で勝手に考えたものです。
こういうときは必ずあることを確認しなければならないのでした。
それは、well-definedかどうか。
well-definedについて馴染みのない方は以下の記事をご覧ください。

また、同型写像は準同型写像のうち、全単射となるもののことを言うのでした。
以上を踏まえると、準同型定理の証明は次の4ステップから組み立てればよさそうだと分かります。
①$\bar{f}$がwell-definedであることの確認
②$\bar{f}$が準同型写像であることの確認
③$\bar{f}$が全射であることの確認
④$\bar{f}$が単射であることの確認
そして、全射であることを示すには像を使うと便利で、
単射であることを示すには核を使うと便利です。
(像と核と全射と単射)
$f$を群$A$から群$B$への準同型写像とする。
また、$A$の単位元を$e_a$とし、$B$の単位元を$e_b$とする。
このとき、以下が成り立つ
・$f$が全射 $⇔$ $Im(f)=B$
・$f$が単射 $⇔$ $Ker(f)=\lbrace e_a \rbrace$
詳細は以下の記事をご覧ください。

では、準同型定理の証明をしていきましょう!
(準同型定理の証明)
$A$を演算$*$についての群、$B$を演算〇についての群とする。
また、$f$は$A$から$B$への準同型写像である。
$f$によって$Im(f)$と$Ker(f)$が定まる。
像の定義より
$Im(f)=\lbrace f(a) \mid a \in A \rbrace$
である。
また、$B$の単位元を$e_b$とすると、
核の定義より
$Ker(f)=\lbrace a \in A \mid f(a)=e_b \rbrace$
である。
$Ker(f)$は必ず$A$の正規部分群になるので、
剰余類を集めた集合
$A/Ker(f)=\lbrace a*Ker(f) \mid a \in A \rbrace$
は、$a, b \in A$を定めたとき、
$(a*Ker(f))・(b*Ker(f))=(a*b)*Ker(f)$
で定まる演算$・$について群となる。
このとき、
$A/Ker(f) \cong Im(f)$を示す。
そのために、
$A/Ker(f)$から$Im(f)$への同型写像が作れることを示せばよい。
いま、$A/Ker(f)$から$Im(f)$への対応付け$\bar{f}$を以下のように定める。
$\bar{f}(a*Ker(f))=f(a)$ $(a \in A)$
$\bar{f}$が$A/Ker(f)$から$Im(f)$への同型写像となることを示す。
まず、$\bar{f}$がwell-definedであることを示す。
そのためには、
$a, b \in A$として、
$a*Ker(f)=b*Ker(f)$のとき、
$\bar{f}(a*Ker{f})=\bar{f}(b*Ker{f})$
であればよい。
いま、$a*Ker(f)=b*Ker(f)$より、
$a*x_1=b*x_2$となる$x_1, x_2 \in A$が存在する。
ただし、
$f(x_1)=e_b$
$f(x_2)=e_b$である。
$a*x_1=b*x_2$より、
$f(a*x_1)=f(b*x_2)$
である。
$f$は$A$から$B$への準同型写像であったので、
$f(a*x_1)=f(b*x_2)$であるとき
$f(a)〇f(x_1)=f(b)〇f(x_2)$
である。
ここで、
$f(x_1)=e_b$
$f(x_2)=e_b$
であったので、
これを
$f(a)〇f(x_1)=f(b)〇f(x_2)$
に代入すると
$f(a)〇e_b=f(b)〇e_b$
となり、$e_b$は$B$の単位元なので
$f(a)=f(b)$である。
ここで、$\bar{f}$の定義より、
$\bar{f}(a*Ker{f})=f(a)$
$\bar{f}(b*Ker{f})=f(b)$
である。
したがって、$f(a)=f(b)$から、
$\bar{f}(a*Ker{f})=\bar{f}(b*Ker{f})$
であることが分かり、$\bar{f}$はwell-definedである…①
次に、$\bar{f}$が$A/Ker(f)$から$Im(f)$への準同型写像であることを示す。
$\bar{f}(a*Ker(f)・b*Ker(f))$
$=\bar{f}(a*Ker(f))〇\bar{f}(b*Ker(f))$
であればよい。
$\bar{f}(a*Ker(f)・b*Ker(f))$
$=\bar{f}(a*b*Ker(f))$
$=f(a*b)$
$=f(a)〇f(b)$
$=\bar{f}(a*Ker(f))〇\bar{f}(b*Ker(f))$
であるので、
$\bar{f}(a*Ker(f)・b*Ker(f))$
$=\bar{f}(a*Ker(f))〇\bar{f}(b*Ker(f))$
成り立つ。
よって、
$\bar{f}$が$A/Ker(f)$から$Im(f)$への準同型写像である…②
次に、$\bar{f}$が全射であることを示す。
$Im(\bar{f})=Im(f)$であればよい。
像の定義より、
$Im(\bar{f})=\lbrace \bar{f}(a*Ker(f)) \mid a*Ker(f) \in A/Ker(f) \rbrace$
である。
$\bar{f}$の定義より、
$\bar{f}(a*Ker(f))=f(a)$である。
よって、
$Im(\bar{f})=\lbrace f(a) \mid a \in A \rbrace$
であることが分かり、
$Im(\bar{f})=Im(f)$
である。
よって像の性質より、
$\bar{f}$は全射である…③
次に$\bar{f}$が単射であることを示す。
そのためには、
$Ker(\bar{f})=\lbrace Ker(f) \rbrace$
であることを示せばよい。
いま、核の定義より、
$Ker(\bar{f})=\lbrace x*Ker(f) \mid \bar{f}(x*Ker(f))=e_b \rbrace$
である。
また、$\bar{f}$の定義より、
$\bar{f}(x*Ker(f))=f(x)$
である。
よって、
$Ker(\bar{f})=\lbrace x*Ker(f) \mid f(x)=e_b \rbrace$
である。
$f(x)=e_b$と$Ker(f)=\lbrace a \mid f(a)=e_b \rbrace$
より、$x \in Ker(f)$である。
ここで、$x*Ker(f)$について考える。
$x*Ker(f)=\lbrace x*a \mid x\in A, a\in Ker(f) \rbrace$
である。
ここで、$Ker(f)$が$A$の正規部分群であることと、$x \in Ker(f)$より、
$x*a \in Ker(f)$である。
したがって、
$x*Ker(f)=\lbrace x*a \mid x*a \in Ker(f) \rbrace=Ker(f)$
である。
$Ker(\bar{f})=\lbrace x*Ker(f) \mid f(x)=e_b \rbrace$
と
$x*Ker(f)=Ker(f)$
より、
$Ker(\bar{f})=\lbrace Ker(f) \rbrace$
である。
$Ker(f)$は$A/Ker(f)$の単位元であるので、
核の性質より、$\bar{f}$は単射である…④
①②③④より、
$\bar{f}$は$A/Ker(f)$から$Im(f)$への同型写像となり、
$A/Ker(f) \cong Im(f)$
となる。
(証明終了)
まとめ
いかがでしたか?
①まず群$A$と群$B$が与えられる。
②$A$から$B$への準同型写像$f$を自分で定める
③すると、$f$によって$Im(f)$と$Ker(f)$が定まる
④$Ker(f)$は核なので、必ず$A$の正規部分群となるため、剰余群$A/Ker(f)$を考えることができる
⑤なんと$A/Ker(f)$から$Im(f)$への同型写像$\bar{f}$を作ることができる(しかも自動的に)
⑥そのため、$A/Ker(f) \cong Im(f)$となる
という流れを押さえていただければと思います。
実用上は、なんかちょっと複雑な剰余群について調べたいときに準同型定理を使います。
シンプルな群との同型写像が見つかると、格段に扱いやすさが上がるからです。
いきなり同型写像を作るのは結構大変ですが、
それよりすこし条件が緩い準同型写像さえ上手く見つけることができれば、
準同型定理より同型写像を自動的に作ることができます。
これが準同型定理の便利さです。
特に、ガロア理論では剰余群がめっちゃ登場します。
方程式が解ける必要十分条件の記述にも剰余群が不可欠です。
そんなとき、準同型定理が大活躍しますので、ご期待ください。
また、今回証明した準同型定理は、第一同型定理とも呼ばれます。
第一があるということは、第二同型定理、第三同型定理も存在します。
次回の記事では、第二同型定理、第三同型定理を扱っていきたいと思いますので、
ご期待ください。
ではまた次回の記事でお会いしましょう!!
参考
画像素材提供(アイキャッチ):kristamoniqueによるPixabayからの画像
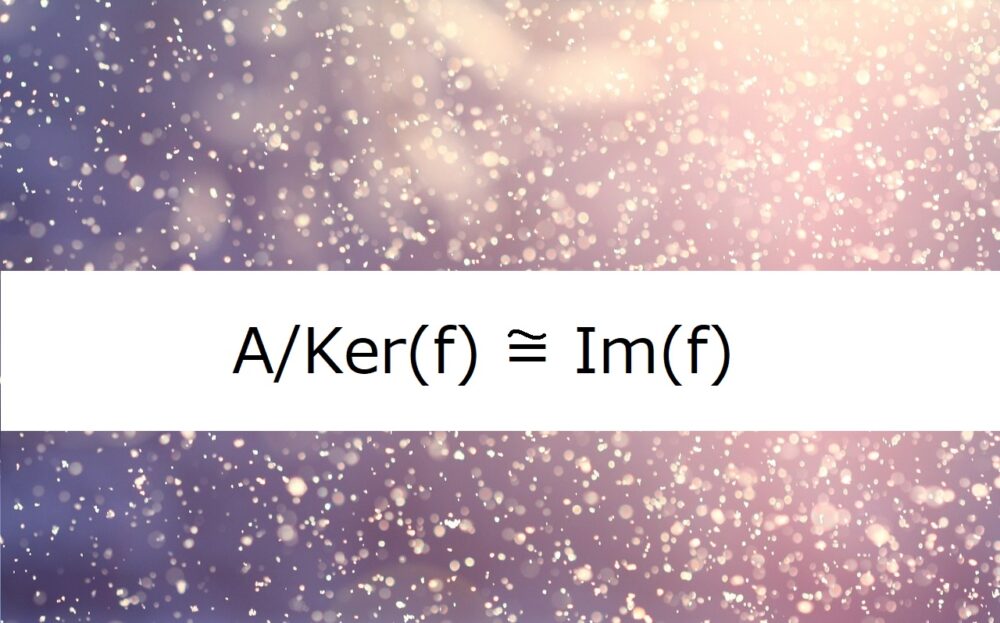
コメント